Магнитное поле в вакууме

Сила, приходящаяся на единицу длины проводника , где b – расстояние между проводниками, – магнитная постоянная.

Величина магнитного поля характеризуется вектором индукции магнитного поля . Магнитное поле возникает при движении зарядов. Принцип суперпозиции: магнитное поле, порождённое несколькими движущимися зарядами, либо несколькими телами равняется векторной сумме магнитных полей, порождаемых каждым из зарядов, или, соответственно, токов в отдельности: . Сила Лоренца . То, что магнитная часть силы Лоренца перпендикулярна скорости, говорит о том, что она не производит работы.

Т.к. , то для постоянного тока при этом , где  – удельное сопротивление проводника, следовательно, 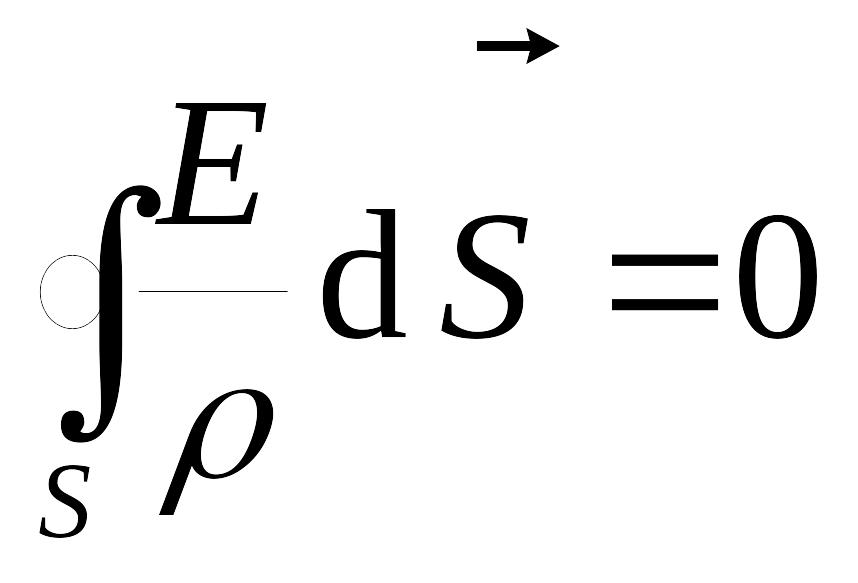, и, т.к. , то , следовательно, заряд в проводнике, по которому идёт постоянный ток не накапливается и притяжение и отталкивание проводников обусловлено не кулоновским взаимодействием.

Сила Ампера

Пусть по двум параллельным проводникам течёт ток. Магнитная часть силы Лоренца, действующей на заряд, , где l – длина проводника, n – концентрации носителей заряда в проводнике, S – площадь поперечного сечения проводника, e – элементарный заряд. Скорость движения этого заряда , где – скорость хаотического теплового движения, – скорость направленного под действием электрического поля. , т.к. . Таким образом, сила Ампера, действующая на объём проводника , по которому течёт ток плотностью в магнитном поле с индукцией . Перепишем , где I – сила тока, текущего по проводнику.

Пусть дан заряд, движущийся со скоростью . Найти , где – радиус-вектор, направленный из заряда в точку, в которой надо найти заряд. Опыт показывает, что .

Для проводника – закон Био-Савара.

Для прямолинейного бесконечно длинного тонкого проводника:

.

.

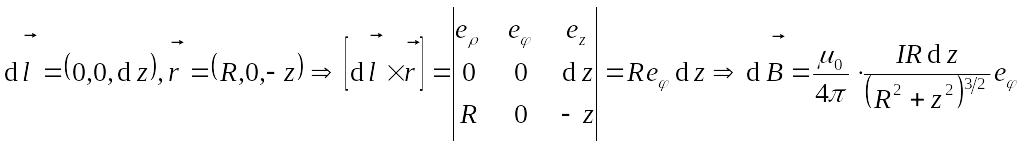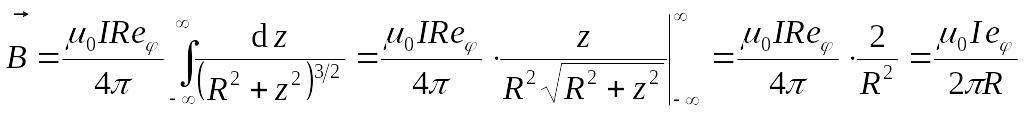Для кольца на его оси:

,

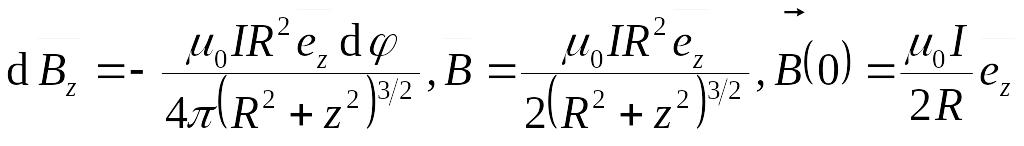– поле в центре кольца.

Теорема Гаусса для поля вектора магнитной индукции: Силовые линии магнитного поля всегда замкнуты, следовательно, если мы возьмём любую поверхность в любом пространстве, то источников линий внутри неё быть не может. Поэтому ил .

Рассчитаем циркуляцию по контуру, составленному из двух меньших контуров:

Ц иркуляция по I контуру: 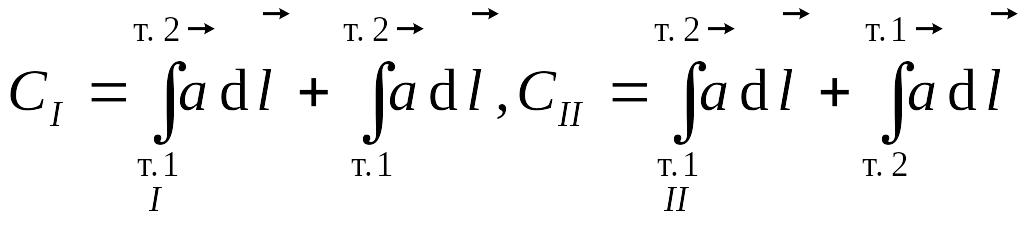, , 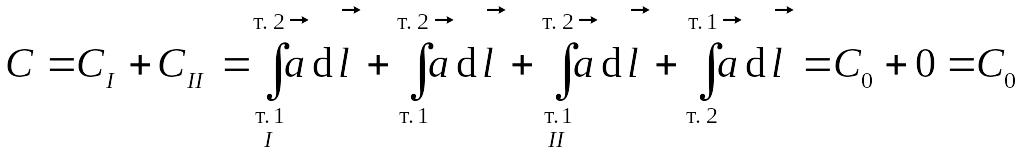следовательно, циркуляция обладает свойствами аддитивности.

Ротор векторного поля – это вектор: .

Выразим в декартовой системе координат:

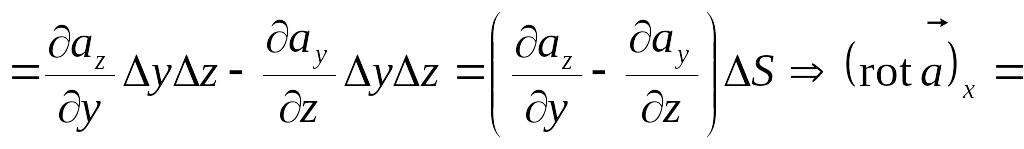
Ц иркуляция Циркуляция . Аналогично , . Циркуляция . После суммирования по всем будет: ( – контур циркуляции) – теоремы Стокса.

Теорема о циркуляции : , где I – сумма всех токов, которые охватываются контуром .

.

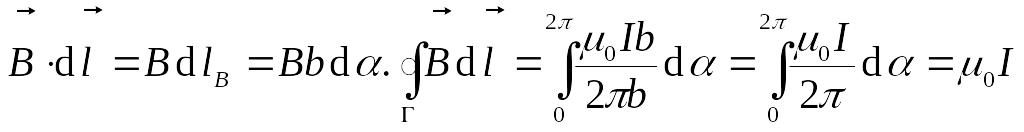Пусть теперь ток не охватывается контуром и касательные, проведённые из точки, где ток пересекает плоскость контура к контуру касаются его в точках 1 и 2. Тогда .

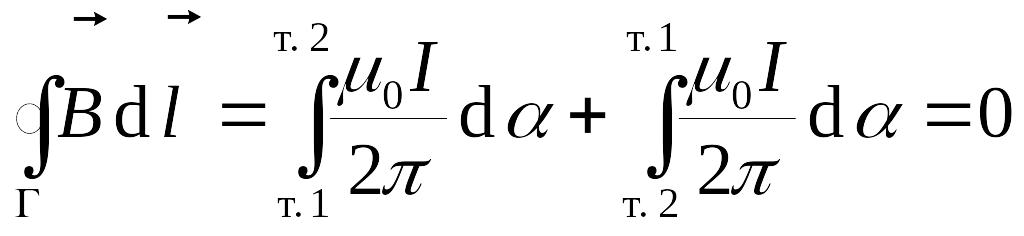Для множества токов . Если ток течёт по объёму, то , где – площадка, перпендикулярная току.

Тогда . Т.к. – любая площадка, то – теорема о циркуляции в дифференциальной форме.

Всё это справедливо только для постоянных токов в вакууме.

Пусть у соленоида n витков на метр и по нему течёт ток I. Докажем, что магнитное поле однородно и внутри, и снаружи соленоида.

. Аналогично . Для контура E будет: . Поток через площадь поперечного сечения соленоида S , где – площадь окружающего пространства: , а – конечная величина, следовательно, , а .

Пусть у тороида N – полное число витков.

Т огда . Т.к. провод обходит центр по кругу, то получается ещё один виток, следовательно, .