
- •21. Магнитное поле и его характеристики. Линии магнитной индукции.
- •22. Закон Био — Савара — Лапласа и его применение к расчету магнитного поля
- •23. Закон Ампера. Взаимодействие параллельных токов
- •24. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля. Магнитное поле движ заряда. Сила Лоренца.Виды движения частицы в м.Поле
- •Магнитное поле движущегося заряда
- •Действие магнитного поля на движущийся заряд
- •Движение заряженных частиц в магнитном поле
- •25. Эффект Холла. Постоянная Холла
- •26. Циркуляция вектора в магнитного поля в вакууме. Магнитное поле прямого тока. Сравнение теорем о циркуляции в и е
- •27. Магнитные поля соленоида и тороида
- •28. Поток вектора магнитной индукции. Магнитный поток через произвольную поверхность. Теорема Гаусса для поля в. Поток вектора в через соленоид.
- •29. Работа по перемещению проводника и контура с током в магнитном поле
- •30. Явление электромагнитной индукции (опыты Фарадея). Закон Фарадея и его вывод из закона сохранения энергии. Вывод закона Фарадея Максвеллом.
- •Закон Фарадея и его вывод из закона сохранения энергии
- •31. Индукционный ток. 3 случая изменения потока магнитной индукции.
- •Вихревые токи (токи Фуко)
- •32. Индуктивность контура. Самоиндукция
- •33. Токи при размыкании и замыкании цепи
- •34. Взаимная индукция. Эдс взаимной индукции. Взаимная индуктивность. Трансформаторы и принцип их работы. Коэфф трансформации и принцип их работы.
- •Трансформаторы
- •35. Энергия магнитного поля. Энергия магнитного поля на примере соленоида. Объемная плотность энергии.
- •36.Электрические токи в атомах и молекулах. Орбитальный момент электрона, сила тока, орбитальный механический момент, гиромагнитное отношение орбитальных моментов, собственный магнитный момент (спин).
- •37. Парамагнетики и диа-магнетики. Намагниченность. Магнитная восприимчивость в веществе. Вектор магнитной индукции результирующего поля в магнетике. Ферромагнетики.
- •Намагниченность. Магнитное поле в веществе
- •Ферромагнетики и их свойства
- •Природа ферромагнетизма
- •38. Теорема о циркуляции вектора магнитной индукции в и вектора напряженности магнитного поля н. Связь в и н. Условия на границе двух магнетиков.
- •Условия на границе раздела двух магнетиков
- •39. Вихревое электрическое поле. Циркуляция вектора напряженности вихревого электрического поля.
- •40. Ток смещения. Полный ток. Полная система уравнений Максвелла для электромагнитного поля.
- •Уравнения Максвелла для электромагнитного поля
- •41. Волновая природа света, принцип Гюйгенса. Законы преломления и отражения света. Когерентность и монохроматичность световых волн.
- •Когерентность и монохроматичность световых волн
- •42. Интерференция света. Методы наблюдения интеференции света. Расчет интерференции от двух источников света.
- •Методы наблюдения интерференции света
- •43. Интерференция света от пластинки постоянной и переменной величины. Кольца Ньютона. Просветление оптики. Интерферометры.
- •Применение интерференции света
- •44.Дифракция света. Принцип Гюйгенса — Френеля. Метод Френеля (зоны Френеля). Дифракции на отверстии и круглом диске.
- •Метод зон Френеля. Прямолинейное распространение света
- •Дифракция Френеля на круглом отверстии и диске
- •45. Дифракция Фраунгофера на одной щели и дифракционной решетке. Условия минимумов и максимумов.
- •Дифракция Фраунгофера на дифракционной решетке
- •46.Критерий Рэлея. Разрешающая способность оптических приборов
- •47. Естественный и поляризованный свет. Закон Малюса. Прохождение света через два поляроида.
- •Поляризационные призмы и поляроиды
- •48. Поляризация света при отражении и преломлении. Закон Брюстера. Поляризационные призмы
- •49. Двойное лучепреломление. Пластинка в четверть длины волны – получение эллиптически поляризованного света.
- •50. Искусственная оптическая анизотропия. Вращение плоскости поляризации
- •Вращение плоскости поляризации
- •51. Дисперсия света. Электронная теория дисперсии Лоренца.
- •Электронная теория дисперсии светя
- •52. Поглощение (абсорбция) света. Закон Бугера-Ламбертаю Виды спектров поглощения.
- •53. Законы теплового излучения (Кирхгофа, Вина, Стефана-Больцмана). Абс черное и серое тело.
- •Закон Кирхгофа
- •§ 199. Законы Стефана — Больцмана и смещения Вина
- •54. Формулы Планка для излучения абс черного тела. Методы оптической пирометрии.
- •Оптическая пирометрия. Тепловые источники света
- •55. Внешний и внутренний фотоэффект.
- •Уравнение Эйнштейна для внешнего фотоэффекта. Экспериментальное подтверждение квантовых свойств света
- •Применение фотоэффекта
Электронная теория дисперсии светя
Из макроскопической
электромагнитной теории Максвелла
следует, что абсолютный показатель
преломления среды
![]()
где
— диэлектрическая проницаемость среды,
— магнитная проницаемость. В оптической
области спектра для всех веществ 1,
поэтому
![]() (186.1)
(186.1)
Из формулы (186.1)
выявляются некоторые противоречия с
опытом: величина n,
являясь переменной (см. § 185), остается
в то же время равной определенной
постоянной
 .
Кроме того, значения n,
получаемые из этого выражения, не
согласуются с опытными значениями.
Трудности объяснения дисперсии света
с точки зрения электромагнитной
теории Максвелла устраняются электронной
теорией Лоренца. В теории Лоренца
дисперсия света рассматривается как
результат взаимодействия электромагнитных
волн с заряженными частицами, входящими
в состав вещества и совершающими
вынужденные колебания в переменном
электромагнитном поле волны.
.
Кроме того, значения n,
получаемые из этого выражения, не
согласуются с опытными значениями.
Трудности объяснения дисперсии света
с точки зрения электромагнитной
теории Максвелла устраняются электронной
теорией Лоренца. В теории Лоренца
дисперсия света рассматривается как
результат взаимодействия электромагнитных
волн с заряженными частицами, входящими
в состав вещества и совершающими
вынужденные колебания в переменном
электромагнитном поле волны.
Применим электронную
теорию дисперсии света для однородного
диэлектрика, предположив формально,
что дисперсия света является следствием
зависимости
от частоты
световых волн. Диэлектрическая
проницаемость вещества, по определению
(см. (88.6) и (88.2)), равна
![]()
где
— диэлектрическая восприимчивость
среды, 0
— электрическая постоянная, Р —
мгновенное значение поляризованности.
Следовательно,
![]() (186.2)
(186.2)
т.е. зависит от Р. В данном случае основное значение имеет электронная поляризация, т.е. вынужденные колебания электронов под действием электрической составляющей поля волны, так как для ориентационной поляризации молекул частота колебаний в световой волне очень высока ( 1015 Гц).
В первом приближении
можно считать, что вынужденные колебания
совершают только внешние, наиболее
слабо связанные с ядром электроны —
оптические электроны. Для простоты
рассмотрим колебания только одного
оптического электрона. Наведенный
дипольный момент электрона, совершающего
вынужденные колебания, равен р=ех,
где е — заряд электрона, х —
смещение электрона под действием
электрического поля световой волны.
Если концентрация атомов в диэлектрике
равна n0, то
мгновенное значение поляризованности
![]() (186.3)
(186.3)
Из (186.2) и (186.3)
получим
![]() (186.4)
(186.4)
Следовательно, задача сводится к определению смещения х электрона под действием внешнего поля Е. Поле световой волны будем считать функцией частоты , т. е. изменяющимся по гармоническому закону: Е = Е0 cos t.
Уравнение вынужденных колебаний электрона (см. §147) для простейшего случая (без учета силы сопротивления, обусловливающей поглощение энергии падающей волны) запишется в виде
![]() (186.5)
(186.5)
где F0
= еЕ0 — амплитудное
значение силы, действующей на электрон
со стороны поля волны,
 —
собственная частота колебаний электрона,
т — масса электрона. Решив уравнение
(186.5), найдем = n2
в зависимости от констант атома (е, т,
0) и
частоты внешнего
поля, т.е. решим задачу дисперсии. Решение
уравнения (186.5) можно записать в виде
—
собственная частота колебаний электрона,
т — масса электрона. Решив уравнение
(186.5), найдем = n2
в зависимости от констант атома (е, т,
0) и
частоты внешнего
поля, т.е. решим задачу дисперсии. Решение
уравнения (186.5) можно записать в виде
![]() (186.6)
(186.6)
где
![]() (186.7)
(186.7)
в чем легко убедиться подстановкой (см. (147.8)). Подставляя (186.6) и (186.7) в (186.4), получим
![]() (186.8)
(186.8)
Если в веществе
имеются различные заряды еi,
совершающие вынужденные колебания с
различными собственными частотами 0i,
то
![]() (186.9)
(186.9)
где т, — масса i-го заряда.
И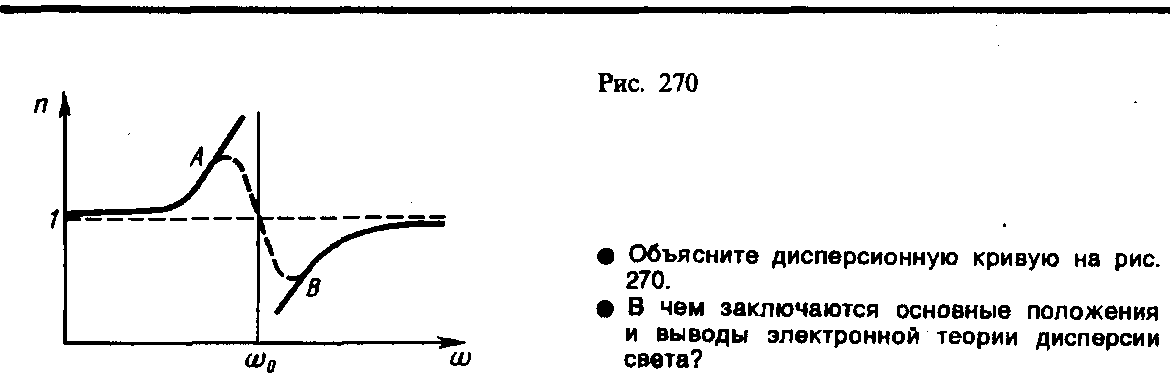 з
выражений (186.8) и (186.9) вытекает, что
показатель преломления n
зависит от частоты
внешнего поля, т. е. полученные зависимости
действительно подтверждают явление
дисперсии света, хотя и при указанных
выше допущениях, которые в дальнейшем
надо устранить. Из выражений (186.8) и
(186.9) следует, что в области от
= 0 до = 0
n2 больше единицы
и возрастает с увеличением
(нормальная дисперсия); при
= 0 n2
= ±; в области от
= 0
до =
n2 меньше единицы
и возрастает от –
до 1 (нормальная дисперсия). Перейдя от
n2 к n,
получим, что график зависимости n
от имеет вид,
изображенный на рис. 270. Такое поведение
n вблизи 0
— результат допущения об отсутствии
сил сопротивления при колебаниях
электронов. Если принять в расчет и
это обстоятельство, то график функции
n()
вблизи 0
задастся штриховой линией АВ. Область
АВ — область аномальной дисперсии
(n убывает при
возрастании ),
остальные участки зависимости n
от описывают
нормальную дисперсию (n
возрастает с возрастанием ).
з
выражений (186.8) и (186.9) вытекает, что
показатель преломления n
зависит от частоты
внешнего поля, т. е. полученные зависимости
действительно подтверждают явление
дисперсии света, хотя и при указанных
выше допущениях, которые в дальнейшем
надо устранить. Из выражений (186.8) и
(186.9) следует, что в области от
= 0 до = 0
n2 больше единицы
и возрастает с увеличением
(нормальная дисперсия); при
= 0 n2
= ±; в области от
= 0
до =
n2 меньше единицы
и возрастает от –
до 1 (нормальная дисперсия). Перейдя от
n2 к n,
получим, что график зависимости n
от имеет вид,
изображенный на рис. 270. Такое поведение
n вблизи 0
— результат допущения об отсутствии
сил сопротивления при колебаниях
электронов. Если принять в расчет и
это обстоятельство, то график функции
n()
вблизи 0
задастся штриховой линией АВ. Область
АВ — область аномальной дисперсии
(n убывает при
возрастании ),
остальные участки зависимости n
от описывают
нормальную дисперсию (n
возрастает с возрастанием ).
Российскому физику Д. С. Рождественскому (1876—1940) принадлежит классическая работа по изучению аномальной дисперсии в парах натрия. Он разработал интерференционный метод для очень точного измерения показателя преломления паров и экспериментально показал, что формула (186.9) правильно характеризует зависимость n от , а также ввел в нее поправку, учитывающую квантовые свойства света и атомов.
