51. Предельные и средние значения пф. Коэффициенты эластичности.

Просчитаем коэф-т эластичности и предельные нормы замещения ф-ов пр-ти. Чтобы оценить влияние прирощения объема ресурсов на изменение объемов пр-ва вводятпонятие показатели частной эластичности выпуска по j-му ф-ру пр-ва или частному ф-ру пр-ва:

Е_j=( f/ x_j)/( f/ x_j)=M_j/A_j (1)

Для малого приращения ∆x_j можно считать, что: E_j=(∆f(x_j)/ ∆ x_j)/(f/ x_j)=(∆f(x_j)/f)*( x_j/∆ x_j)=(∆f(x_j)/f)/(∆ x_j/ x_j) (2)

Такое преобразование ф-лы (2) позвол эконом смысл понятию частичной эластичности. Дробь, стоящ в числителе, - относит прирост объема выпуска пр-ва. Дробь, стоящ в знаменат, - относит прирост j-го ф-ра.

ij – доля %-та, на кот возраст выпуск пр-ции при увелич объма ф-ра пр-ва на 1%.

Исходя из ф-лы (1) м вычислить эк-ий смысл коэф-тов а₁ и а₂.

Е₁= а₁, Е₂= а₂, У= а₀К^а1 - L^1-а1

∑ частных эластичностей по всем ресурсам – эластичного пр-ва Е_х=∑ E_j (3)

Когда анализируется выход пр-ии, зависящий от вектора ресурсов, какова норма замещ 1г рес-са другим В , отражающая эту норму, обозначающая -R_ij=-dx_j/dx_i (4). Знак «-» запис-ют потому что уменьшение заменяемого i-го рес-са требует роста заменяющего j-го рес-са д/сохр пр-ва. Т.к. н аизокванте знач ПФ пост велич, то можно высч-ть полный диф-ал ф-ии, кот для случая 2х перемен имеет след вид:

, ,

- / =( )/( )

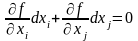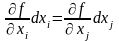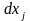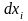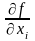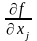R_ij=М_i/Mj

Предельная норма замещения i-го рес-са j-м опред как отнош частн эластичностей выпуска.

M_j=Е_iA_i=[f(x_i)/ x_i]

M_j=Е_jA_j=Е_j [f(x_j)/ x_j]

R_ij=Е_i (f(x)/ x_i) / Е_j [f(x)/ x_j]= (Е_i/ Е_j)/( x_j/ x_i)

Для ф-ии Кобба-Дугласса

Е_K=a₁ Е_L=a₂ У= а₀К^а1L^а2

R_LK= (Е_L / Е_K)*(K/L)=(a₂/a₁)*(K/L)

Предельная норма L замещ труда капиталом пропорц капиталовооруж труда.

С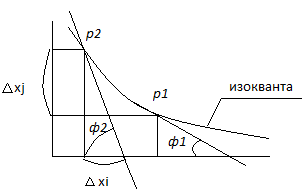 графической точки зреия коэф R_ij, представл собой tg угла наклона касат изокванты.

Для хар-ки скорости изменения предельн нормы замещ испоьз коэф-т, кот наз эластичность замещения ф-ра. Обычно его расм для 2х ф-ых ф-ий Кобба-Дугласса. Капиталовооруж= K/L=k, поэтому

Ϭ_LK=(dk/K)/(d R_LK/ R_LK)=d(lnk)/d(R_LK). Чем больше эластичность замещ, тем больше возм-ть замещ 1го рес-са др.

52. Пф ces с постоянной эластичностью замещения факторов.

Для хар-ки скорости изменения предельн нормы замещ испоьз коэф-т, кот наз эластичность замещения ф-ра. Обычно его расм для 2х ф-ых ф-ий Кобба-Дугласса. Капиталовооруж= K/L=k, поэтому

Ϭ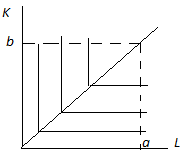 _LK=(dk/K)/(d R_LK/ R_LK)=d(lnk)/d(R_LK) (1). Чем больше эластичность замещ, тем больше возм-ть замещ 1го рес-са др. Для ф-ции К-Д, для кот а₁+а₂=1, Ϭ_LK=1. Ее наз ф-ей с пост эластичн-ю замещ. В некот случ принципиально невозм замещ ф-ий, т.е. они должны использ в опред пропорции. В этом случ эласт-ть замещ = 0 и эти ПФ наз-ся ф-ции Леонтьева и изокванты этих ф-ий м.б. представл след образом.

У=min(aK,bL) (2)

Общее выраж для ф-ии с пост эласт-ю, учит св-ва однород ф-ции и имеет след вид: У=А(uK^-ρ + (1-u) L^-ρ)^{-n/ ρ} , ρ≥-1, n – степень однородности

53. Использование пф в эк-ом анализе.

Производственные функции позволяют количественно проанализировать важнейшие экономические зависимости в сфере производства. Они дают возможность оценить среднюю и предельную эффективность различных ресурсов производства, эластичность выпуска по различным ресурсам, предельные нормы замещения ресурсов, эффект от масштаба производства и многое другое.

54. Пр-во товаров потребления. Ф-ция полезности, св-ва, кривые безразличия

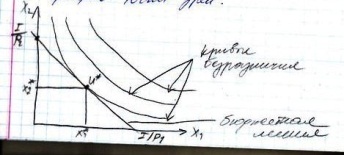
Применим методы теорий пр-ных ф-ций к изучению теор потребл. Потребители-П стремятся MAX удовлетвор св потребностей при заданных бюджетных ограничениях. Конкретной природой потребностей будем пренебрегать. Простр. тов П наз множ-во всех товаров, благ и услуг, доступных потреб-лю. Ограничимся кол-вом тов (n) и буд рассматр х=(х₁,х₂,…,х_n) – вектор товаров. Считается, что для любых 2-ух наборов товаров потреб-ль может сказать, что один из них более предпочтительнее или что он не видит меж ними разницы, т.е. на пр-ве вводится отношение предпочтения х₁<х₂ (предпоочтительнее х₂). Ф-ция кот выраж предпочтение потр-ля наз ф-ция полезности. Ее св-ва: 1)ðu/ðx_i >0, прирост люб блага при неизм кол-ве остальн только улучшает потреб оценку. Эту производную наз предельными полезностями. ðu/ðx_i =М_i.

2) ð²u/ðx_i²<0, предельн полезность продукта уменьш, когда увелич объем его потребления, это св-во выраж убывание предельн полезности.

3) ð²u/ðx_i ðx_j>0,полезность кажд продукта растет, если растет кол-во др продукта(ели только они не могут замещ др друга).

Рассматриваемые 2 продукта и ф-ция полезности, приним-щая постоян знач в кажд точке при измен кол-в этих продуктов, наз кривая безразличия.

55.Модель задачи потребит выбора и ее св-ва

Цены продуктов р1 и р2 и бюдж огранич велич I.Тогда задача отыскаия max ф-ции полезн при заданном бюдж огранич: u=u(x1,x2)→max

P1x1+p2x2≤I.Графич:

Отнош предельн полезн товаров в оптим точке = отнош их рыночных цен;

L(x1,x2,λ)=u(x1,x2)+λ(I-p1x1-p2x2)

M1/M2=P1/P2. Составл полный дифференциал для бюдж линии:

- ðх2/ðх1=Р1/Р2. Предельная норма замены 1-го продукта другим б равна отнош их рыночных цен.

Аналогично ф-ция спроса: х1^*=d1(I,p1,p2)

Х2^*=d2(I,p1,p2), зная аналитич выраж ф-ции полезности можно записаить как ф-ции дохода и рын цен.

56. Предельная полезность и предельная норма замещения полезности благ

Прирост люб блага при неизм кол-ве остальн только улучшает потреб оценку. Эту производную наз предельными полезностями. ðu/ðx_i =М_i.

ð²u/ðx_i²<0, предельн полезность продукта уменьш, когда увелич объем его потребления, это св-во выраж убывание предельн полезности.

Когда анализируется выход продукции, зависящей от вектора ресурсов, важно знать, какова норма замещения одного рес-са другим, в частности какие нужны затраты капитала для сокращения затрат труда на 1 ед-у. Величина,, отражающая эту норму: R_ij= - dx_j/dx_i. Знак «-», потому что уменьшение заменяемого i-го рес-са требует увеличение замещающего j-го рес-са для сохранения объёма пр-ва.

R_ij = M_i/M_j (1).

Предельная норма замещения определяется как отношение частных эластичностей выпуска. M_i=E_iA_i=E_i* f(x)/x_i , M_j=E_jA_j=E_j* f(x)/x_j. Подставим в (1):

R_ij = [E_i* f(x)/x_i]/ [E_j* f(x)/x_j] = E_i/E_j * x_j/x_i

57. Модель Стоуна – наиболее известная из ф-ции полезности

Имеет вид:

u(x)=П (x_i-a_i)^αi, a_i>=0, α_i.0, i=1,n, u(x)→max

П – произведение, α – хар-т относительное значение каждого блага для потребителя, a – min необходимое кол-во блага.

Набор a=(a1, a2,…an) возможно приобрести, если доход потребителя I≥∑p_ia_i, p – цена блага. Если выполняется I=∑p_ia_i, то задача максимизации не имеет смысла. Задача максимизации:

u(x)=П (x_i-a_i)^αi→max

I=∑p_ix_i.

Составим ф-цию Лагранжа:

L(x, λ)=П (x_i-a_i)^αi + λ(I-∑p_ix_i). Зная относительную ценность каждого блага, потребиітель хочет распорядіться деньгамі, чтобы максімізіровать полезность. Вычіслім частные производные от ф-ции Лагранжа по каждому благу и приравняем к 0:

(x^α)’=αx^α-1

∂L/∂x_i= [α_iu(x)/(x_i-a_i)]-λp_i=0 разделим на х:

x_i=a_i+αu(x)/λp. Умножим на λр и просуммируем:

λ∑px=λ∑pa+u(x)∑α.

∑px=I

λI= λ∑pa+u(x)∑α.

Ф-ция полезности:

u(x)=(λI/∑α)-( λ∑pa/∑α)

x=a+(αλ(I-∑pa))/λp∑α

x=a+(α/∑α)*(I-∑pa)*(1/p)

58. Взаимозаменяемость благ и эффекты компенсации. Уравнение Слуцкого

Для того, чтобы учесть многообразн формы спроса строят неск ф-ций. Ф-цию для предметов 1-ой необходимости, для благ обыденного спроса,для прдметов роскоши.Если увелич цены на к-либо товар приводит к сниж спроса на этот тов и на др, то тов наз взаимодополняемые. Если при повыш цены на к-либо тов или благо одноврем повыш спрос на др тов, то говорят, что тов взаимозамен. Сост табл завис измен спроса на тов от цены:

Измен дохода ---------- Измен цены	Ценные ðхi/ðI>0	Малоценные ðхi/ðI<0
Нормальные ðхi/ðрi <0	Масло слив, олив, говядина	Маргарин, раст масло
Гиффина ðхi/ðрi >0		Картофель свекла, морковь

Реал взаимозамен тов может выраж измен благосост: если j-ое благо может заменить i-ое в потреблении, т спрос на него может расти в результ падения дохода.Тогда использ понятие компенсированного изменения цены, кот позвол поддерж прежний ур-нь благосост, несмотря на повыш цены на тов.

I=pixi+pjxj. В примере благо I явл ценным и нормальным - с повыш цены спрос на него уменьш. При правильной организации цен точка В должна находиться выше и левее точки начального равновесия. В общем случае изменение спроса на любой товар в результате взаимодействия эффектов замены и дохода описывается ур-м Слуцкого.

Ур-е Слуцкого было введено в 1915 г и является основным в теории потребительского выбора, имеет вид:

∂х_i / ∂p_j = (∂х_i / ∂p_j )_комп – (∂х_i / ∂I)*x_j i,j =1,n.

В левой части уравнения общий эффект от влияния изменения цены j-го товара на спрос на i-й товар. (∂х_i / ∂p_j )_комп – влияние замены, т.е.влияние компенсированной цены. Частная производная рассчитывается из условия компенсации роста цены за счёт увеличения дохода. (∂х_i / ∂I)*x_j - означает влияние изменения дохода. Ур-е Слуцкого используется в макроэкономике для количественного расчёта степени взаимозаменяемости или взаимодополняемости. Если первое слагаемое положительное, то товары – взаимозаменяемые, если отрицательное – взаимодополняемые.

59. Выбор критерия оптимизации

Система критериев: (ВЕЗДЕ в ∑ j =1,n)

1. Показатель прибыли:

f₁ = ∑(Ц_j-С_j)x_j

2. Показатель прибыли с учётом рентабельности:

f₂ = (∑(Ц_j-С_j)x_j )/ (∑y_jx_j + Ф_осн )

3. Показатель прибыли с обобщённым учётом рентабельности:

f₃ = (1/ (Ф_об + Ф_осн))* ∑(Ц_j-С_j)x_j

4. Показатель прибыльности с учётом производительности труда

f₄ = (1/S)* ∑Ц_jx_j

5. Стоимостной показатель:

f₅ = ∑Ц_jx_j ,

где n – количество изделий

j – индекс изделия

x_j – объём выпуска

с_j – себестоимость изделия

Ц_j – оптовая цена изделия

S – средняя производительность труда

y_j – норматив оборотных средств на j-е изделие

Ф_об – среднегодовая стоимость оборотных средств

Ф_осн - среднегодовая стоимость основных средств

Поэтому экономические задачи планирования и управления производством называются многокритериальными.

60. Система ограничений экономико-математической модели

На пяду с многокритериальностью ограничения разбиваются на группы по свонму экономическому смыслу:

1. Ограничение на кол-во сырья

g_i(x)≤b_i i=1,m

g_i(x)=∑a_ijx_j j=1,n

A=[a_ij], m- количество видов сырья, n – матрица нормативов затрат.

2. Ограничения по времени работы оборудования и по производственным площадям. Если учитываются затраты на приобретение нового оборудования, то в ограничения включаются условия целочисленности.

3. Ограничения по трудовым ресурсам

4. Взаимосвязь между отдельными видами продукции, обусловлен. технологией производства

5. Показатели, определяющие ход деятельности предприятия (величина затрат на ед. стоимость продукции, выработка продукции на единицу з/п)

61. Компромиссные методы векторной оптимизации

Предположим, что следует решить задачу с большим кол-вом групп ограничений. Поскольку min f= - max (-f), то будем считать, что все критерии максимизируются. Составим вектор критериев с системой ограничений:

F(f₁, f₂,…f_k) →max (1)

g_i(x)≤b_i i=1,m.

Предположим, что точки максимума, определённые для каждого критерия x^*_j, не совпадают, тогда решение задачи (1) может быть только компромиссным. При решении компромиссных экономических задач используются след. методы:

1. М-д, основанный на свёртывании критериев

2. М-д, использующий ограничения на критерии

3. М-ды, основанные на компромиссах.

Перед их применением критерии сводят к единой единице измерения или безразмерной величине. Для этого применяют 2 способа:

1. f_k (x)= f_k (x)/ f_k ^*, k=1,K

2. f_k (x)= [f_k ^*- f_k (x)]/ f_k ^*.

В методе свёртывания каждому критерию присваивается весовой коэффициент и получается обобщённая линейная комбинация критериев

F₁ = ∑α_kf_k(x) (2), ∑α_kf_k=1, k=1,K

Решения, полученные в результате оптимизации ф-ции (2), являются эффективными. Недостаток м-да: малым приращениям α соотве-т большие приращения F₁.

Самый распространённый м-д, использующий ограничения на критерии, - м-д уступок. Его алгоритм: критерии расставляют в порядке убывания их важности и решается задача

f₁(x)→max

g_i(x)≤b_i

f₁^*(x^*)

устанавливается уступка ∆₁ по этому критерию в % от значения. Далее решается задача

f₂(x)→max

g_i(x)≤b_i

f₁(x)≥f₁^*-∆₁

определяют f₂^*(x^*) и ^*∆₂. Решают задачу:

f₃(x)→max

g_i(x)≤b_i

f₁(x) ≥f₁^*-∆₁

f₂(x)≥f₂^*-∆₂.

Ещё одной разновидностью м-да является м-д равных и наименьших отклонений. Рассмотрим критерии f₁ и f₂ и решим задачу f₁(x)→max, f₂(x)→max, g_i(x)≤b_i . f₁-? f₂-?

Будем считать, что отклонение [f₁^*- f₁(x)]/[ f₂^*- f₂(x)]= k₁/k₂. Тогда:

k₁f₁^*-k₂f₁(x)= k₁f₂^*- k₁f₂(x)

k₁f₂(x)-k₂f₁(x)= k₁f₂^*- k₂f₁^*. Тогда решается след задача:

f₃(x)→max

g_i(x)≤b_i

k₁f₂(x)-k₂f₁(x)= k₁f₂^*- k₂f₁^*

Приведенные выше методы позволяют организовать принятие математически обоснованных решений.