49. Производственная ф-ция Кобба-Дугласа

Самой использ производств ф-цией явл-ся произв ф-ия Кобба-Дугласа (ПФКД). У=а₀К^а1L^a2 (1).

Парметры ф-ции а₀, а₁, а₂>0. При емат обраб данных Кобб и Дугласс обнаруж а₁+а₂≈1. Если нужно иссл-ть влияние только 1го из ф-ров, то др ф-ры фиксио на опред ур-не. Предположим, что объем живого труда, к-ый косвенно отраж квалиф работников на протяж некоторого врем, не измен на протяж опред врем. Тогда а₀L^a2=с₀ – const ф-ция (1) примет вид: У= с₀К^а1. Если удвоить объем осн-го капит при неизмен числ-ти раб и квалиф, мы не сможем получить удвоение объема сов пр-та, а₁<1, а₀К^а1=c₁.

У= L^a2с₁ – если ф-ция зафиксир.

Удваивая числ-ть раб мыне сумеем получить удвоение объема пр-ва, а₂<1. Поэтому ф-лу (1) перепиш а₁+а₂=1, У=а₀К^а1L^1-а1 (2) . Разделим обе части ф-лы (2): , У/ L =а₀К^а1 (L^1-а1/ L), У/ L =а₀(К/ L) ^а1 (3)

У/ L =Z – производ-ть труда, К/L=k – капиталовооруженность труда, Z=a₀k^a1 (4). В реальности пр-ть считает от роста капиловооруж. 0<a₁<1 Обобщение ф-лы (1) служит динамич модель ф-ии Кобба-Дугласса сущ НТП.

У(t)=a₀c^pt(K(t))^a1(L(t))^1-a1 (5)

c^pt – множитель, учитывающ НТП.

50. Св-ва ПФ. Графики ПФ, линии уровня ПФ.

Сформулир общ св-ва произв ф-ии:

1. При отсутствии хотя бы 1го из ресурсов пр-во невозможно. F(x₁,x₂,…,0,…,x_n)=0 (1) x_j=0, j=1,n

2. С ростом затрат любого ресурса при неизмен кол-ве др ресурсов объем пр-ва возраст:

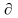f/ x_j>0, j=1,n (2)

3. Величина прироста выпуска на кажд допол ед ресурса может только убывать. Закон убывающ эф-ти мат формы записи м.б. представлен как f/ x_j≤0, j=1,n (3)

4. При увеличении одного из ресурсов объем др ресурса возраст f/ x_j x_i >0 i, j=1,n i≠ j (4)

5. ПФ явл-ся однородной степени р>0, по кажд из аргументов. Для упрощ будем считать, что для всех аргументов степень однородности одинакова f(t x) = t^p f(x) (5), х=(х₁,х₂,…,х_n). При р>1 имеем рост эф-ти пр-ва от роста масштаба пр-ва; при р<1 имеем падение эф-ти пр-ва от роста масштаба пр-ва; при р=1 имеем постоянную эф-ть пр-ва при росте его масштаба.

Л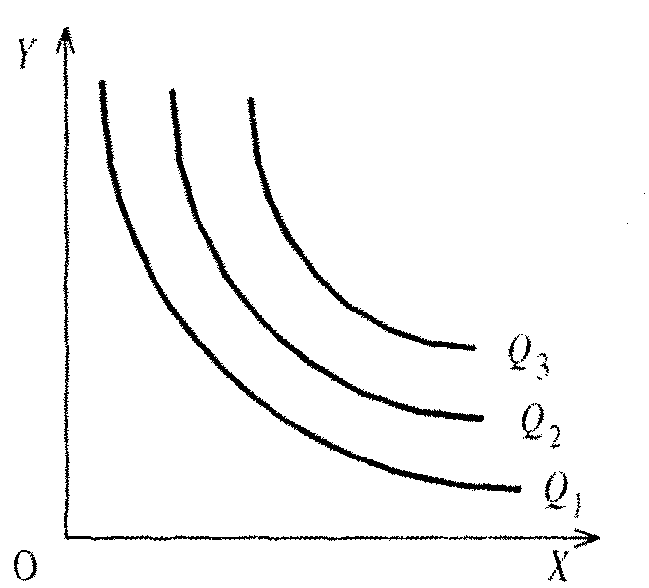 иния уровня ПФ – это множество точек, на котором ПФ принимает постоянное значение. Иногда линии уровня называют изоквантами ПФ. Возрастание одного фактора и уменьшение другого могут происходить таким образом, что общий объем производства остается на прежнем уровне. Изокванты как раз и определяют все возможные комбинации факторов производства, необходимых для достижения заданного уровня продукции. Из рисунка видно, что вдоль изокванты выпуск продукции постоянный, то есть прирост выпуска отсутствует. Математически это означает, что полный дифференциал ПФ на изокванте равен нулю:

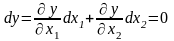. Отрицательный наклон изоквант объясняется тем, что увеличение использования одного фактора при определенном объеме выпуска продукта всегда будет сопровождаться уменьшением количества другого фактора.