46. Применение балансовых моделей в задачах менеджмента: прогнозирование затрат ресурсов, объема и отраслевой стр-ры валового выпуска, прогнозирование затрат труда.

Базовая прогнозная модель нах примен при оценке разл эл-ов стоим-ой стр-ры пр-ва. В рамках данной модели б. полагать, что инфляц процесс хар-ся кол-но индексами среднеотрасл-ых цен р_i . Через q_i обозн индекс измен добавл ст-ти, обуслов-го влиянием ценового ф-ра при условии неизмен реальн объемов пр-ва и стр-ры межотраслевого обмена. С 1м и 3м квадрантом получим след табл:

Отрасли-произ-ли	Отрасли-потреб
1	X11*p1	X12*p1	X13*p1
2	X21*p2	X22*p2	X23*p2
3	X31*p3	X32*p3	X33*p3
	∑хi1* pi	∑хi2* pi	∑хi3* pi
	Z1*p1	Z2*p2	Z3*p3
Вал.выпуск	X1*p1	X2*p2	X3*p3

Базовая прогнозн модель для оценки последствия инфляций запис в след виде:

х11р1+х21р2+х31р3+z1q1=x1p1

x12p1+x22p2+x32p3+z2p2=x2p2 (10)

x13p1+x23p2+x33p3+z3p3=x3p3

Если в рав-ве (10) замен отраслевые поставки. Ур-ие (10) примет след вид: x_ij=a_ijX_j , а11Х1р1+а21Х1р2+а31Х1р3+z1q1=X1P1 (11). Рав-во (11) кажд из ур-ий делят на соотв объем валового выпуска, тогда обознач ч-з 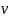_I отнош z_i /x_i : _I = z_i /x_i (12), т.е. отнош добавл ст-ти к валов выпуску и наз его нормой добавл ст-ти, соотн (11) мы запишем в матричн ф-ме: P=А^Т Р+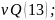 P= ; = ;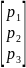

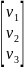Q= [q1, q2, q3]. А^Т – транспонир матр прямых материал затр мы получим вектор с, он м.б. опред из рав-ва:

р= (Е- А^Т)^-1 Q (14).

Зная матрицу норм расхода ресурсо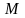в , можно рассчитать матрицу полных затрат ресурсов 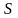, перемножив матрицы .

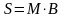Эк-ий смысл матрицы S состоит в том, что элемент, S_ij стоящий на пересечении i – ой строки и j – го столбца, показывает, какое суммарное кол-во i– го ресурса необходимо для того, чтобы j – ая отрасль могла выпустить ед-цу конечной пр-ии.

Потребность П в пр-ции всех отраслей матер-го пр-ва для получения ед-цы конечного продукта j – го вида можно найти, просуммировав эл-ты матрицыB по столбцам

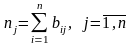
Затраты труда, необходимые для пр-ва ед-цы пр-ции, складываются из затрат живого и овеществлённого труда. В простейшем случае затраты труда будем представлять в ед-цах труда одинаковой степени сложности.

Пусть L_j — затраты живого труда в производство X_j единиц j – го продукта. Тогда tj коэф-т прямых затрат труда на ед-цу j – го вида пр-ции составит

Обозначим через T_j полные затраты труда на ед-цу j – го продукта. Полные затраты труда на пр-во ед-цы j – го вида пр-ции могут быть представлены ф-лой

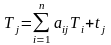
В матричном виде 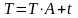, окончательно получим

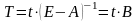
т.е. для расчёта вектора полных затрат труда T для заданного вектора прямых трудовых затрат t следует этот вектор умножить на матрицу полных матер-ых затраt B.