45. Коэф-ты прямых, полных и косвенных материальных затрат, их свойства

Коэф прямых затрат м.б. расчит:

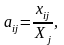
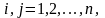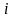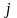(1) и хар-ет кол-во пр-ии -ой отрасли, кот необх для пр-ва ед-цы валовой пр-ции -ой отрасли. Если в ф-ле (1) = , то мы имеем коэф-т собств затрат. В случае 3х агрегир отраслей матрица коэф-тов прям затрат:

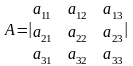- Матриуа коэф-тов пряых затрат.

Из (1) 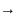ф-ла = 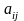* 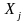(2) и с использованием этой ф-лы модель МОБ м.б. написана в виде:

х₁₌а₁₁х₁+а₁₂х₂+…+а_1nх_n+у₁ х₂₌а₂₁х₁+а₂₂х₂+…+а_2nх_n+у₂ (3)

х₃₌а_n1х₁+а_n2х₂+…+а_nnх_n+у_n

Модель (3) наз базовая прогнозная модель МОБ, связ-ая отраслевую стр-ру валового выпуска и конечного спроса. Модель (3) м.б. переписана в матрич. форме

Х=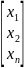 , вектор конечн. продукции, У= .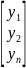

Х =АХ+У (4). В моделях (3) и (4) предполаг, что матрица А изв-на, потому что коэф-ты прямых затрат хар-ют в обобщ виде технолог пр-ва на макроуровне и учит инновац технолог. процессов можно предположить сохран неизмен коэф в теч некот-го п-да. Сист (3) и (4) содержат 3 ур-ия и 6 перемен-х, поэтому для однознч реш сист необход задать 3 велич. тогда остальные опр-ся из реш сист на основании моделей (3) и (4), производят след варианты расчета:

1. Задана валовая продукция отраслей. Треб определить вектор конечного использования

2. В модели задан вектор конечного использования. Треб рассчит какой следует обеспечитить валовый выпуск.

3. Модели заданы по одним отраслям объемы валовой пр-ии, по др конечный выпуск. Треб рассч остальные знач.

Из эк-го смысла изв-ми полагают валовую пр-ию энергетической и топливной пром-ти, а также конечн спрос на пр-ию отраслей потребит комплекса, т.е. на пр-ию легкой и пищевой пр-ти. Для реш 1й з-чи модель (4) преобраз след образ: Х-АХ=У; (Е-А)Х=У

Х=(Е-А)^-1 У (5)

Матр (Е-А)^-1 наз матрица полных затрат и обознач В, для сущ-ия такой матр необх-м треб-ем явл-ся продуктив-ть матрицы, для того, чтобы матрица А была продуктивной, необх потр-ть, чтобы выполнилось огранич на велич ее нормы, т.е. наибольш из   ∑ эл-ов матрицы по столбцу

maх j ( 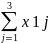)≤1 (6) . Усл (6) явл-ся достат, но необх. Матр А м.б. продуктив если ∑ эл-ов по столбцу превосх 1. Выясним эк-ий смысл коэф-ов полных затрат. Для этого соотнош (5) перепишем в разверн виде, обозначая эл-ты матр В через b_ij :

Х₁=b₁₁*Y₁+ b₁₂* Y₂+ b₁₃*Y₃

Х₂=b₂₁*Y₁+b₂₂*Y₂+b₂₃*Y₃ (7)

Х₃= b₃₁*Y₁+ b₃₂*Y₂+ b₃₃*Y₃

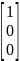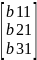Предположим, что конечная пр-ия пр-ся только в 1й отрасли в ед объема, т.е. У= . Поставл вектор в сист ур-ий (7), получим Х= . Эл-ты первого столбца матр полных затр показ кол-во валовой пр-ии 1й отрасли необход для того, чтобы 1 ед пр-ции отправить в конечный спрос. В общ виде коэф b_ij показ объем валовой пр-ии отрасли с номером i , необх для того, чтобы 1ед пр-ии отрасли с номером i отправить в конечн использов. Если матрица А продуктивна, то для матр (Е-А)^-1 справедливо разлож в ряд Неймана: В=(Е-А)^-1=Е+А+А²+А³+А⁴+… (8). Для матр Х м. записать след разлож: Х=У+АУ+А(АУ)+А(А²У)+… (9). Разложение (9) показывает, что валовый выпуск вкл конечн пр-ию, прямые затр на пр-во конечн пр-ии и начиная с 3го слогаемого косвенные затраты. Для понимания смысла косв затр нарис схему:

Хлеб: мука и электроэн….мука: электроэн и зерно КЗ1….зерно: электроэн и семена КЗ2.

Т.о. понятно назв матр полных затрат, следует отметить, что матр в рав-ве (8) имеет все более уменьшь коэф-т по мере увелич порядка косвен затр. Для 3го и 4го пор коэф матр мало отич от 0.