7. Прямые и обратные функции.

Рассмотрим функцию . Очевидно , т. е. каждому значению из ставится в соответствие одно или несколько значений . Значит, на множестве задана однозначная или многозначная функция от , которая называется обратной функцией к функции и обозначается . В этом случае функция называется прямой функцией.

Замечание. У обратной функции - независимая переменная, - зависимая.

Примеры.

1. Рассмотрим функцию . , . Возьмем произвольно. Соответствующее ему будет таким, что , откуда , т.е. - обратная функция для функции . Обратная функция в данном примере, очевидно, однозначная.

2. Рассмотрим функцию . , . Возьмем произвольно. Соответствующее ему будет таким, что , откуда , где , т.е. , где , - обратная функция для функции . Обратная функция в данном примере, очевидно, многозначная.

Определение. Говорят, что функция имеет обратную функцию , если последняя – однозначная.

Таким образом, функция - имеет обратную, а - не имеет.

Вопрос. А как же ?

Пример. Рассмотрим функцию , у которой .

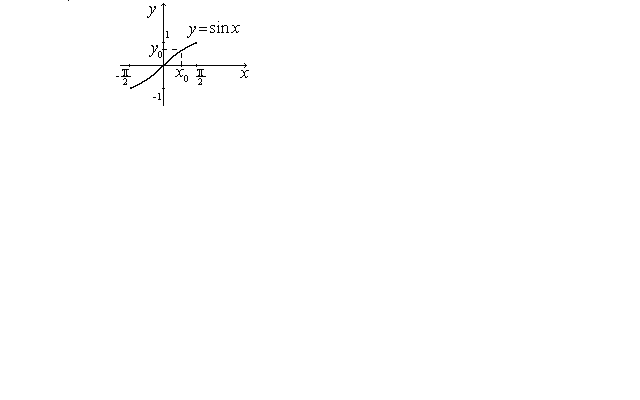У нее . Возьмем произвольно. Соответствующее ему , т.е. - обратная функция для функции , у которой . Обратная функция уже будет однозначной.

Замечание. Аналогично функции обратных функций не имеют, а имеют обратные функции , , .

Теорема. Пусть функция является обратной к функции . Тогда график функции получается из графика функции в результате симметрии последнего относительно прямой .

Пример. , , . Построим график функции .

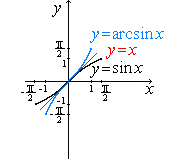
Задание. Построить графики остальных обратных тригонометрических функций.

1 Квантор «: » переводится как «для которых выполняется условие:» или «такие, что».

2 Данное свойство называется неравенством треугольника.

3 Квантор « » переводится так: «равносильно», «эквивалентно».

4 Квантор « » переводится так: «для любого(любой)».

5 Квантор « » переводится так: «найдется(существует)».