Математический анализ Множества
Определение. Множество – это совокупность объектов, называемых элементами множества.
Множества
обозначаются большими латинскими
буквами:
;
их элементы – малыми латинскими буквами:
.
Если
элемент
принадлежит множеству
,
то этот факт записывают так:
,
если не принадлежит, то так:
или
.
Примеры.
1.
- множество натуральных чисел;
-
множество целых чисел;
-
множество рациональных чисел;
-
множество действительных чисел.
2.
Если
и
,
то
-
отрезок 1;
-
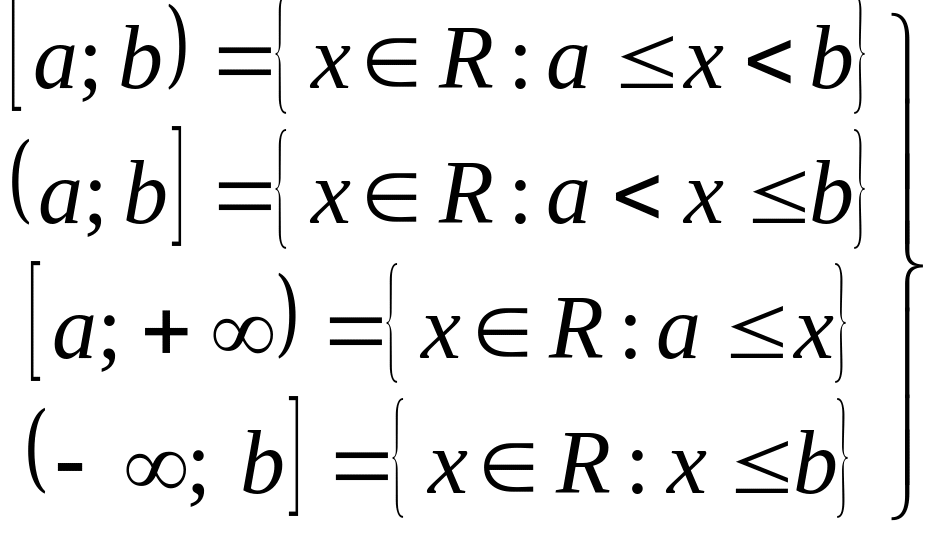полуинтервалы;
-
интервалы.
Определение. Отрезки, полуинтервалы, интервалы называются промежутками.
Определение.
Множество, не содержащее ни одного
элемента, называется пустым и обозначается
.
Определение.
Множество
называется подмножеством множества
,
если все элементы множества
принадлежат множеству
.
Если множество
является подмножеством множества
,
то этот факт обозначают так:
.
Примеры.
1.
2.
Определение.
Множества
и
называются равными, если
,
а
.
Если множества
и
равны, то этот факт обозначают так:
.
Операции над множествами
Определение.
Объединением
множеств
и
называется множество, состоящее из всех
элементов, принадлежащих хотя бы одному
из этих множеств. Объединение множеств
и
обозначается так
.
Пример.
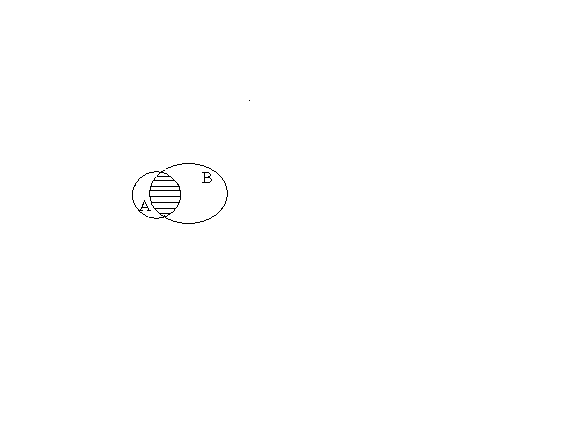
Определение.
Пересечением множеств
и
называется множество, состоящее из всех
элементов, принадлежащих каждому из
этих множеств. Пересечение множеств
и
обозначается так
.
Пример.
Определение. Разностью множеств и называется множество, состоящее из всех элементов множества , не принадлежащих множеству . Обозначается так: \ .
Пример.
\
Определение.
Если
содержится в
,
то разность
\
называется дополнением множества
до множества
.
Этот факт обозначается так:
.
Пример.
Абсолютная величина действительного числа или модуль действительного числа
Определение.
Абсолютной величиной действительного
числа
(или модулем числа
)
называется само число
,
если
,
или число
,
если
.
Обозначается модуль числа
так:
.
Т.о.
=
Свойства модуля.
.
.
.
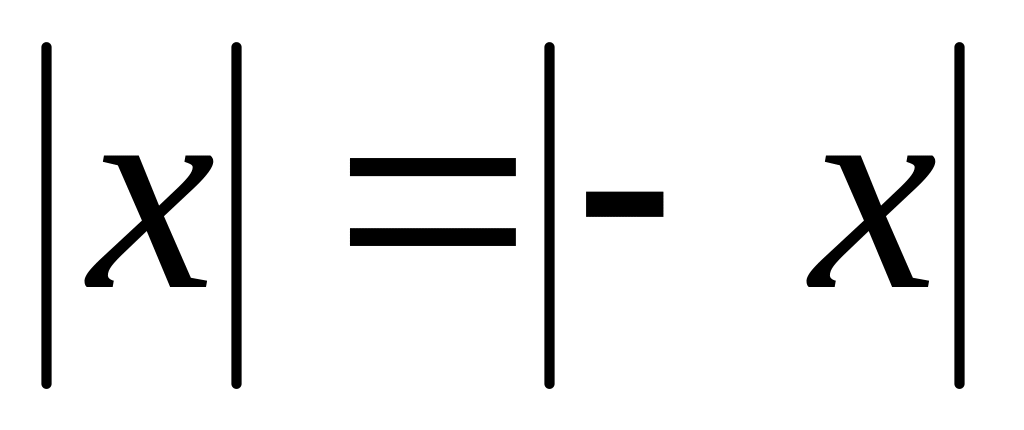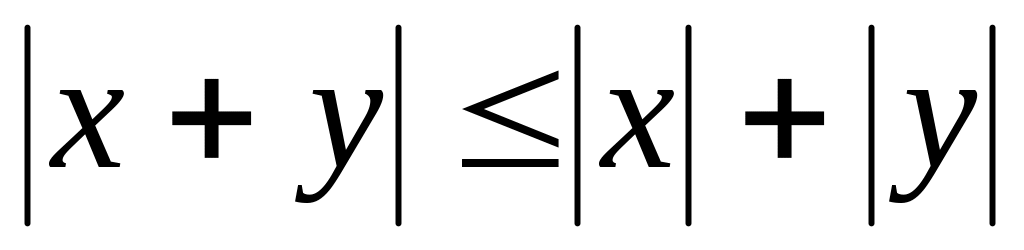2
.
.
.
.
3
.
Функция с одной переменной
Определение.
Если каждому значению величины
из некоторого множества
по какому-либо правилу закона
ставится в соответствие одно определенное
значение величины
,
то говорят, что на множестве
задана функция
от
и обозначают ее так:
.
В этом случае величина
называется независимой переменной или
аргументом;
-
зависимой переменной или функцией;
множество
-
областью определения функции и
обозначается
.
Определение.
Совокупность всех значений, принимаемых
величиной
,
называется областью значений функции
и обозначается
.
Определение.
Если
,
,
то функция
называется числовой.
В дальнейшем, говоря о функции, мы будем подразумевать, что она числовая.
Вопрос. Почему в определении функции от требуется, чтобы каждому значению величины ставилось в соответствие одно определенное значение величины ? А если несколько, можно ли считать такую зависимость функцией?
Пример.
Рассмотрим функцию
.
Очевидно, что здесь, каждому значению ставится в соответствие два значения .
Определение. Если каждому значению величины из некоторого множества по какому-либо правилу закона ставится в соответствие одно определенное значение величины , то говорят, что на множестве задана однозначная функция от ; более одного – многозначная функция от .
Т.о., зависимость из приведенного примера также можно считать функцией, только многозначной. Однако любую многозначную функцию можно свести к однозначным, которые анализировать, очевидно, легче. Поэтому, когда говорят о функциях, имеют в виду однозначные.
Пример.
Многозначную
функцию из предыдущего примера можно
представить виде двух однозначных
функций:
и
.
