9.Автокорреляция случайных возмущений, их последствия, обобщенный метод наименьших квадратов.

Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Те между ними есть зависимость.

Есть положительная автокорреляция, где за положительным отклонением следует положительное, за отрицательным – отрицательное. Отрицательная автокорреляция - за положительным чаще всего следует отрицательное.

Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов

Причина – неправильный выбор спецификации модели.

Последствия автокорреляции

- оценки коэффициентов теряют эффективность;

- стандартные ошибки коэффициентов занижены

Типы автокорреляции

Модели с автокоррелированными остатками называются авторегрессионными. Рассматриваем модель парной регрессии,

Авторегрессия 1-го порядка: AR(1)

Авторегрессия 5-го порядка: AR(5)

Автокорреляция скользящих средних 3-го порядка:

10. Принципы спецификации эконометрических моделей и их содержание.

Первый принцип спецификации эконометрической модели является универсальным принципом метода математического моделирования. Принцип заключается в том, что спецификация модели возникает в результате трансляции на математический язык взаимосвязей исходных данных экономической задачи (экзогенных переменных модели) и ее искомых неизвестных (эндогенных переменных модели). В процессе такой такой трансляции опираются на законы экономической теории, которые, по возможности, стараются описать линейными алгебраическими функциями.

Второй принцип требует, чтобы количество уравнений, составляющих спецификацию модели, в точности совпадало с количеством эндогенных переменных, включенных в модель.

Модель, возникающая на этапе спецификации, как правило, имеет структурную форму, отражающую заложенные в модель экономические утверждения. В такой форме эндогенные переменные модели, как правило, не выражены явно через ее экзогенные переменные. При помощи алгебраических преобразований модель от структурной формы может быть трансформирована к приведенной форме, где каждая эндогенная переменная представляется в виде явной функции только экзогенных переменных модели. Приведенная форма модели непосредственно предназначена для прогноза (объяснения) эндогенных переменных при помощи экзогенных переменных. В частном случае структурная форма модели может совпадать с приведенной формой.

11. Метод наименьших квадратов, основные понятия и определения. Расчет оценок параметров уравнения парной регрессии методом наименьших квадратов

Метод наименьших квадратов. Этот метод был предложен Гауссом

еще в 18 веке. Гаусс решал задачу о том, как на плоскости (в пространстве)

через известный набор точек провести прямую наилучшим способом. В

качестве критерия он предложил использовать сумму квадратов остатков

(невязок), т.е. разностей между абсциссами реальных точек и

соответствующих им точек, лежащих на прямой. В математике решение

такой задачи получило название регрессионного анализа.

Расчет оценок параметров уравенения парной регрессии МНК:

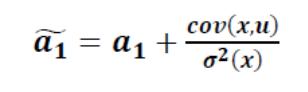Математическое ожидание оценки параметра равно правой части выражения , т.к. параметр и количественных характеристики случайных переменных константы.