Тема 8. Двоїстість в лінійному програмуванні

8.1 Двоїста задача

8.2 Основні теореми двоїстості

8.3 Отримання розв’язку задачі за розв’язком її ДЗ

8.4 Економічна інтерпретація пари двоїстих задач

8.5 Цінність ресурсів

8.6 Двоїстий симплекс–метод

8.1 Двоїста задача

Двоїста задача – це ЗЛП, яка формулюється за допомогою певних правил безпосередньо з умов початкової (прямої) задачі.

Розглянемо узагальнене формулювання двоїстої задачі ЛП, що може бути застосовне до будь-якої форми представлення початкової задачі. У її основу покладений той факт, що використання симплекс-метода вимагає приведення будь-якої ЗЛП до канонічної форми (усі обмеження – обмеження–рівності, усі змінні – невід’ємні). Таким чином, формулювання двоїстої задачі, що приводиться нижче, є узагальненим в тому сенсі, що воно може бути застосовано до усіх форм початкової задачі. Як буде показано нижче, при такому формулюванні двоїстої задачі автоматично враховуються знаки двоїстих змінних, що в інших випадках нерідко викликає непорозуміння.

Нехай маємо пряму ЗЛП в канонічній формі:

при обмеженнях

Відмітимо, що до складу змінних включаються також надлишкові і залишкові змінні.

8.1.1 Правила побудови двоїстої задачі

Двоїста задача виходить шляхом структурного перетворення умов прямої задачі відповідно до наступних правил:

1) Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі.

2) Кожній змінній прямої задачі відповідає обмеження двоїстої задачі.

3) Коефіцієнти при деякій змінній прямої задачі (стовпець), стають коефіцієнтами лівої частини відповідного обмеження двоїстої задачі (рядком).

4) Коефіцієнт при змінній у виразі для цільової функції прямої задачі, стає коефіцієнтом правої частини відповідного обмеження двоїстої задачі.

5) Напрям оптимізації, обмеження і знаки двоїстих змінних формуються згідно таблиці 1.

Таблиця 1

Напрям оптимізації ЦФ ПЗ у канонічній формі	ДЗ
Напрям оптимізації ЦФ ПЗ у канонічній формі	ЦФ	Обмеження	Змінні
Максимізація	Мінімізація		Не обмежені у знаку
Мінімізація	Максимізація		Не обмежені у знаку

Тут і надалі прийняті наступні скорочення: ПЗ – пряма задача, ДЗ – двоїста задача.

Схематично, зв’язок між задачами зображено на рисунку 1.

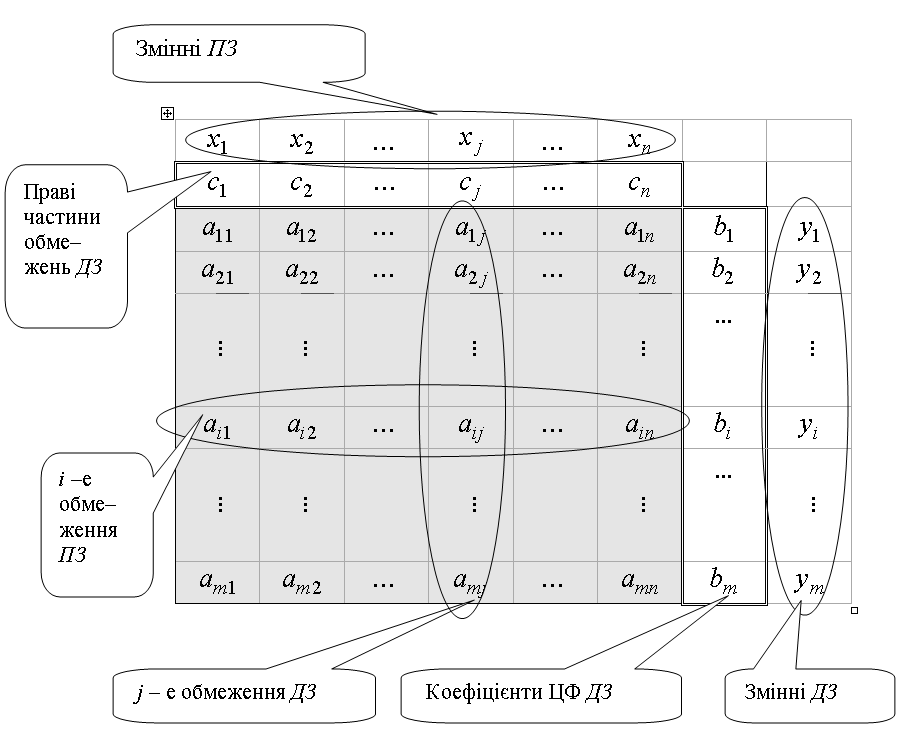
Рисунок 1

Таким чином, ДЗ має змінних ( ) і обмежень (що відповідають змінним ПЗ).

Якщо двоїсту задачу розглядати як початкову (пряму), то відповідна їй двоїста задача збігатиметься з прямою. Тобто пряма і двоїста задача є взаємно-двоїстими, тому про них говорять як про пару двоїстих задач.

Далі ми розглядатимемо дві пари двоїстих задач – симетричні і несиметричні.