6.4.1 Схема двохетапного методу Етап I
I.1. Ввести в обмеження штучні змінні, необхідні для отримання початкового розв’язку
I.2.
Записати нову цільову функцію, що
передбачає мінімізацію суми всіх
введених штучних змінних
.
I.3. Розв’язати задачу лінійного програмування
ЯКЩО
мінімум нової цільової функції
виявляється більше нуля, початкова
задача не має допустимих розв’язків,
і процес обчислень закінчується.
ІНАКШЕ (всі штучні змінні мають в оптимумі нульові значення), початкова задача має допустимі розв’язки.
Можливі наступні випадки:
1. ЯКЩО всі штучні змінні є небазисними, то перейти до етапу II. У поточній точці надлишкових обмежень немає.
2. ЯКЩО всі штучні змінні дорівнюють нулю, але серед них є базисні, то в поточній точці є надлишкові обмеження.
ЯКЩО
при цьому в рядку
,
відповідному штучній змінній, є коефіцієнт
,
де
відповідає небазисній не штучній
(основній або додатковій) змінній, то
ми можемо вивести з базису цю штучну
змінну і ввести замість неї змінну
.
2.а ЯКЩО такий процес виведе з базису всі штучні змінні, то отримаємо вироджене допустиме рішення початкової задачі. Таким чином в поточній точці є надлишкові обмеження (але при цьому немає лінійно-залежних). Перейти до етапу II.
2.б
ЯКЩО ж, навпаки, такий процес не виведе
всі штучні змінні з базису, то кожен
рядок
,
відповідний штучній змінній, в якому
для
всіх нештучних змінних (основних або
додаткових), відповідає
надлишковому обмеженню, яке є лінійною
комбінацією інших обмежень.
Ці обмеження потрібно виключити і
перейти до етапу II.
Етап II
Виключити з моделі штучні змінні, викресливши з таблиці відповідні стовпці.
Оптимальний базисний розв’язок, отриманий на етапі I, використовувати як початковий розв’язок вихідної задачі.
Для
спрощення викладу матеріалу ми на кроці
1 етапу I
вводили штучну змінну в кожне обмеження.
На практиці при побудові початкового
ДБР спочатку формується частина одиничної
матриці
,
наскільки це можливо, із стовпців,
відповідних основним
і залишковим
змінним. А потім частина цієї матриці,
що залишилася, доповнюється стовпцями,
що відповідають штучним змінним.
Розглянемо приклади використання двохетапного методу.
Приклад 1
Нехай маємо математичну модель:
|
(1) |
|
(2) |
|
(3) |
|
(4) |
Приведемо задачу до канонічної форми:
|
(5) |
|
(6) |
|
(7) |
|
(8) |
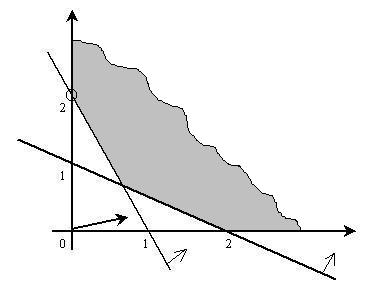
Рисунок 3
Етап I
1.
Введемо штучні змінні в обмеження (2) і
(3) (бо початково ці обмеження мали вигляд
“”).
Позначимо штучні змінні
та
відповідно. Тоді модель (5)–(8) прийме
такий вигляд:
|
(9) |
|
(10) |
|
(11) |
|
(12) |
2.
На першому етапі двохетапного методу
необхідно мінімізувати допоміжну ЦФ
.
В нашому випадку:
.
Виразимо
та
із рівнянь (10), (11) відповідно:
Підставимо
ці вирази в цільову функцію
:
Перетворюємо її до наступного вигляду:
3. Будуємо початкову симплекс-таблицю двохетапного методу. Рядок заповнюємо відповідно до виразу, який було знайдено на попередньому кроці. ЦФ (9) перетворюється до вигляду:
після чого заповнюємо –рядок таблиці.
Базисними змінними є змінні та .
Базисні змінні |
|
|
|
|
|
|
Розв’язок |
|
(min) |
3 |
3 |
–1 |
–1 |
0 |
0 |
4 |
|
|
–3 |
–1 |
0 |
0 |
0 |
0 |
0 |
|
|
2 |
1 |
–1 |
0 |
1 |
0 |
2 |
2 |
|
1 |
2 |
0 |
–1 |
0 |
1 |
2 |
1 (min) |
Тепер
розв’яжемо задачу табличним
симплекс–методом, приймаючи рядок
–
рядком цільової функції, а над рядком
будемо виконувати ті ж самі перетворення,
що й над звичайними обмеженнями, що
дозволить нам по закінченню етапу І
отримати повну інформацію про початковий
ДБР етапу ІІ. Згідно умови оптимальності
для задачі на мінімум у базис вводиться
змінна, котрій відповідає додатна
відносна оцінка (додатний коефіцієнт
–рядка).
В нашому випадку в базис можна ввести
як
так і
.
Оберемо для цього змінну
.
Згідно умови допустимості виводимо з
базису змінну
.
Після виконання операції заміщення отримуємо таблицю:
Базисні змінні |
|
|
|
|
|
|
Розв’язок |
|
(min) |
3/2 |
0 |
–1 |
1/2 |
0 |
–3/2 |
1 |
|
|
–5/2 |
0 |
0 |
–1/2 |
0 |
½ |
1 |
|
|
3/2 |
0 |
–1 |
1/2 |
1 |
–1/2 |
1 |
2/3 (min) |
|
1/2 |
1 |
0 |
–1/2 |
0 |
1/2 |
1 |
2 |
Оскільки не всі коефіцієнти цільової функції не додатні, то продовжуємо ітерації симплекс–методу. Згідно умови оптимальності вводимо в базис змінну та згідно умови допустимості виводимо з базису змінну . В результаті отримуємо таблицю:
Базисні змінні |
|
|
|
|
|
|
Розв’язок |
(min) |
0 |
0 |
0 |
0 |
–1 |
–1 |
0 |
|
0 |
0 |
–5/3 |
1/3 |
5/3 |
–1/3 |
8/3 |
|
1 |
0 |
–2/3 |
1/3 |
2/3 |
–1/3 |
2/3 |
|
0 |
1 |
1/3 |
–2/3 |
–1/3 |
1/3 |
2/3 |
В останній таблиці виконується умова оптимальності для цільової функції , тобто ми отримали розв’язок, в якому ця функція досягає мінімуму. Оскільки оптимальне значення функції дорівнює нулю, початкова задача має допустимий розв’язок – переходимо до етапу II.
Етап II
Стовпці та а також рядок видаляємо з поточної таблиці, після чого розв’язуємо задачу табличним симплекс–методом, минимізуючи вже цільову функцію .
Базисні змінні |
|
|
|
|
Розв’язок |
|
(min) |
0 |
0 |
–5/3 |
1/3 |
8/3 |
|
|
1 |
0 |
–2/3 |
1/3 |
2/3 |
2 |
|
0 |
1 |
1/3 |
–2/3 |
2/3 |
– |
З
гідно
умови оптимальності вводимо в базис
змінну
,
згідно умови допустимості виводимо з
базису змінну
.
Отримуємо таблицю:
Базисні змінні |
|
|
|
|
Розв’язок |
(min) |
–1 |
0 |
–1 |
0 |
2 |
|
3 |
0 |
–2 |
1 |
2 |
|
2 |
1 |
–1 |
0 |
2 |
Ця таблиця – оптимальна, тому що в рядку коефіцієнти при небазисних змінних – від’ємні (виконується умова оптимальності для задачі на мінімум). Задача розв’язана.
Відповідь: =0, =2, min = 2.
Приклад 2
Початкова ЗЛП |
ЗЛП в канонічній формі |
Додаткова ЗЛП |
|
|
|
.
.
.Розв’язок
На рисунку 4 задача розв’язана графічно.
|
Рисунок 4 |
Штучна змінна вийшла з базису. Відкидаємо рядок, що відповідає допоміжній ЦФ , та стовпчик, що відповідає штучній змінній , і продовжуємо процес розв’язання задачі.
БЗ |
|
|
|
|
Розв’язок |
(max) |
-10 |
0 |
0 |
-6 |
6 |
|
2 |
0 |
1 |
1 |
2 |
|
-1 |
1 |
0 |
-1 |
1 |
(max) |
2 |
0 |
6 |
0 |
18 |
|
2 |
0 |
1 |
1 |
2 |
|
1 |
1 |
1 |
0 |
3 |
Відповідь:
= 18,
=
0,
= 3.