Тема 6 Методи пошуку початкового дбр

6.1 Знаходження ДБР ЗЛП в стандартній формі

6.2 Штучний початковий розв’язок

6.3 М-метод

6.4 Двохетапний метод

6.1 Знаходження дбр для злп в стандартній формі

Нехай маємо ЗЛП в стандартній формі («всі обмеження виду ‘≤ ’»):

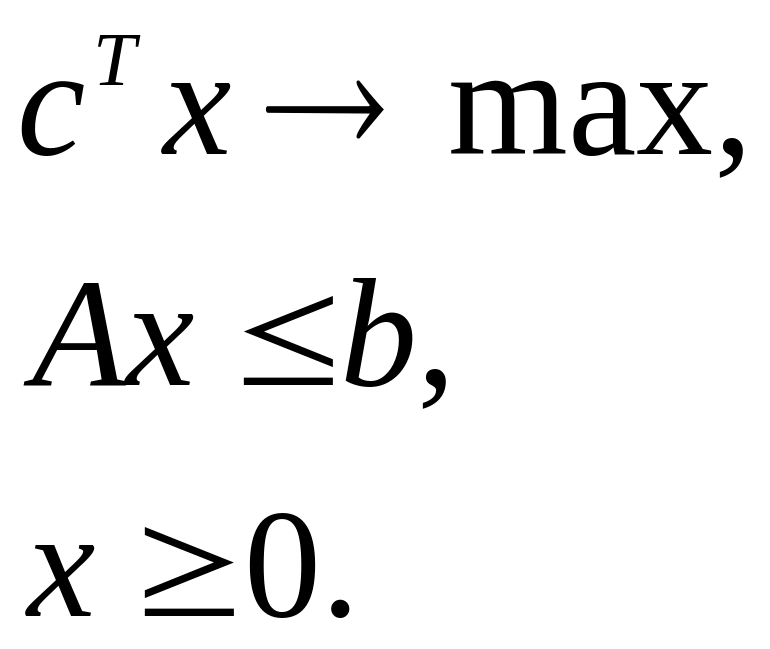
Припустимо, що . Приведемо початкову задачу до канонічної, ввівши з цією метою залишкові змінні . Хай – вектор залишкових змінних. Тоді ЗЛП в канонічній формі:

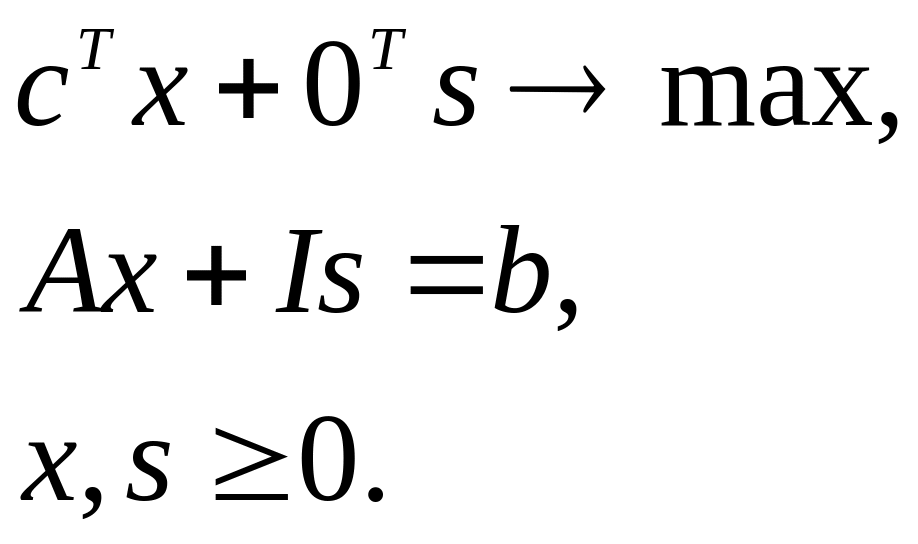
Очевидно, що вектор є допустимим базисним розв’язком даної задачі – і може бути взятий за початковий розв’язок.

Переваги такого підходу:

–– Якщо , то початковий розв’язок є допустимим.

–– Немає проблем з пошуком оберненої матриці: .

–– Перетворена задача будується елементарно.

Перетворена задача в загальному випадку має такий вигляд

,

,

.

В нашому випадку:

ЦФ: .

Обмеження:

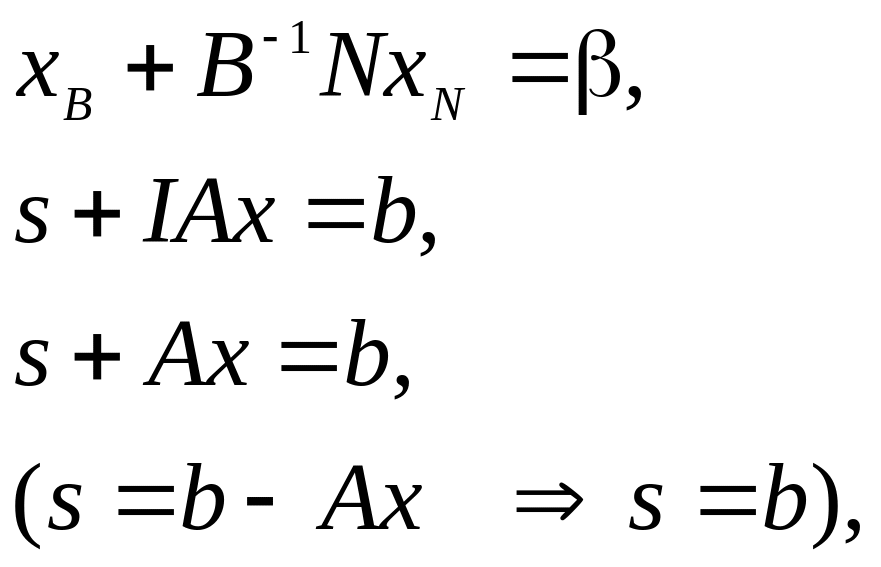
Разом перетворена задача для початкового ДБР така:

,

,

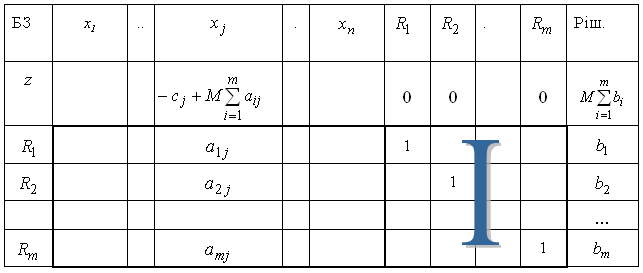
А симплекс-таблиця, відповідна початковому ДБР, має вигляд:

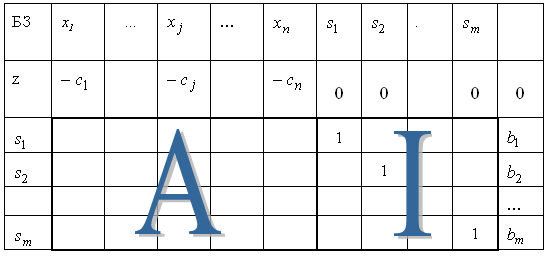
6.2 Штучний початковий розв’язок

Хай маємо ЗЛП в канонічній формі:

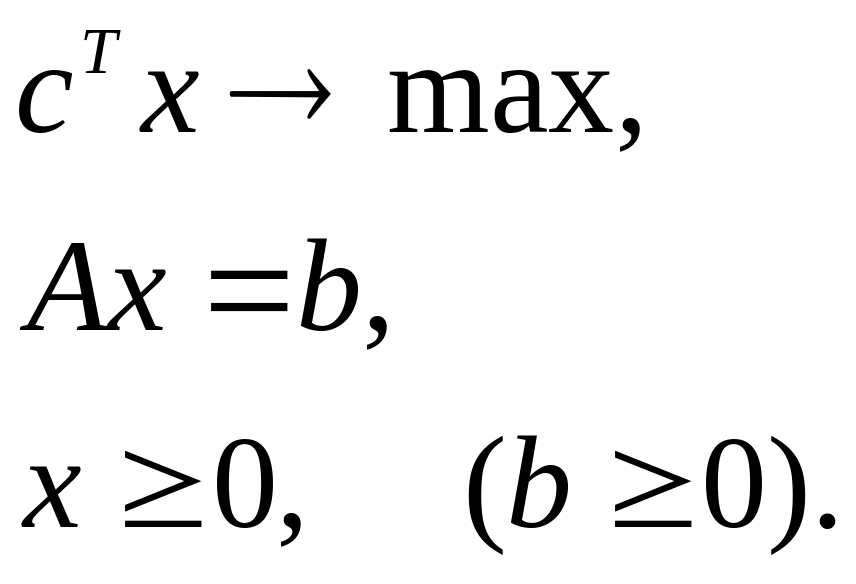
Ідея підходу припускає включення невід’ємних змінних в ліву частину кожного з рівнянь, що не містять «очевидних» початкових базисних змінних, тобто тих змінних, які входять тільки в одне рівняння з коефіцієнтом 1 (у симплекс-таблиці їй відповідає одиничний стовпець ).

Введемо в -е рівняння невід’ємну змінну :

,

,

…

,

…

.

Оскільки ці змінні не мають відношення до змісту поставленої задачі, вони отримали назву «штучних». Визначимо вектор штучних змінних:

.

Тоді система обмежень в матричній формі має вигляд: .

Штучні змінні забезпечують отримання початкового базису, тобто виконують ту ж роль, що і залишкові змінні (тобто вони використовуються тільки для отримання «стартової» точки).

Т.ч. початкове штучне рішення: .

Введення штучних змінних допустимо тільки в тому випадку, якщо відповідна схема обчислень змушуватиме ці змінні набувати нульових значень в кінцевому оптимальному розв’язку, забезпечуючи допустимість оптимуму. Для цього потрібно накласти «штраф» за використання штучних змінних. Розроблені два тісно зв'язаних між собою методи отримання початкового ДБР, в яких використовується «штрафування» штучних змінних:

–– -метод (або метод великих штрафів);

–– двохетапний метод.

6.3 - метод

В цьому методі штучні змінні вводяться в обмеження так, як це описано в п. 6.2. При введенні ж до складу ЦФ кожній змінній приписується штраф – достатньо великий по модулю від’ємний коефіцієнт . Такий спосіб введення штучних змінних приводить до наступної лінійної моделі:

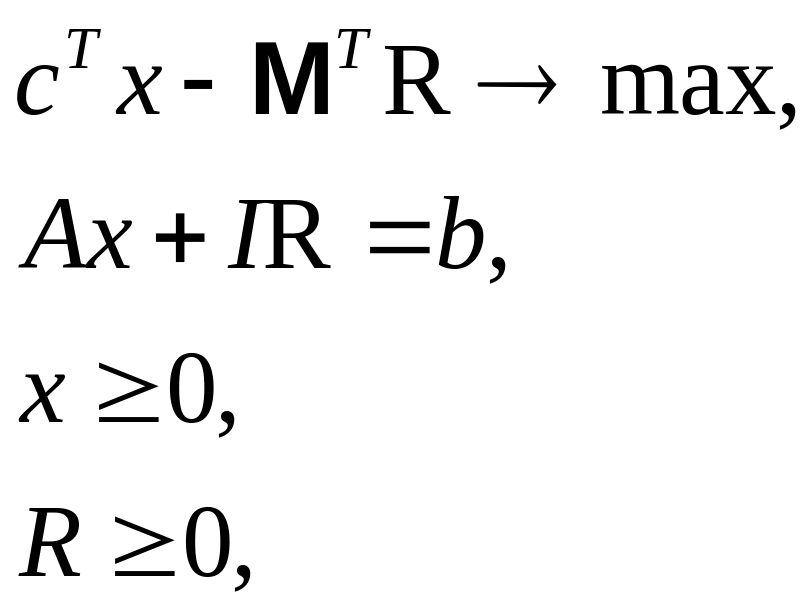
де вектор , .

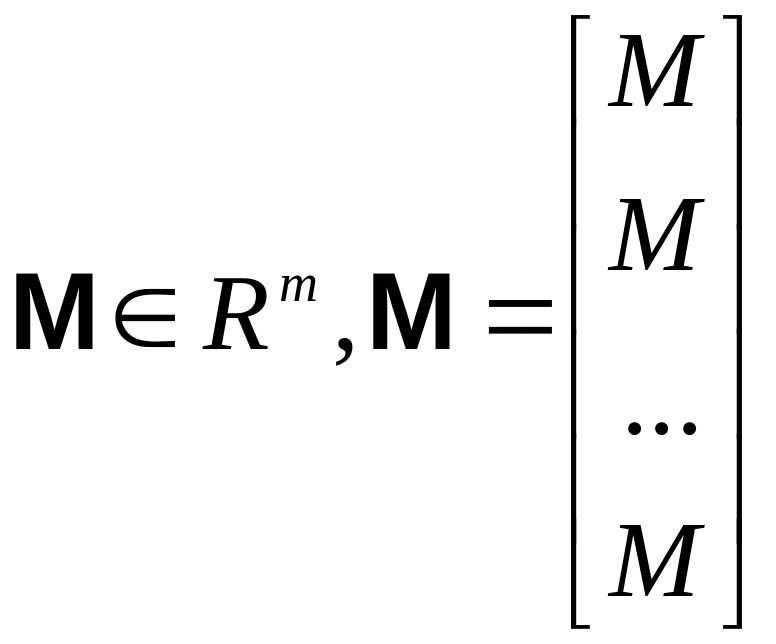У задачі на мінімум кожній змінній приписується достатньо великий додатній коефіцієнт .

Розглянемо тепер, яким чином «нова» структура моделі автоматично приводить до того, що на кінцевій стадії процесу оптимізації змінні набувають нульового значення. Оскільки ми маємо справу із задачею на відшукання максимуму, а змінним у ЦФ приписаний великий по абсолютній величині коефіцієнт , то метод оптимізації, направлений на знаходження максимального значення ЦФ, приведе до того, що змінні в оптимальному розв’язку перетворяться у нуль.

Визначимо компоненти перетвореної задачі, відповідній початковому розв’язку, в якому :

.

Числові значення ДБР (значення базисних змінних і відповідне значення ЦФ):

,

.

Компоненти вектора відносних оцінок небазисних змінних:

,

коефіцієнт при небазисній змінній :

( – сума коефіцієнтів вектор–стовпця ).

При застосуванні табличного симплекс-метода після отримання початкового ДБР необхідно перетворити - рядок так, щоб початковий розв’язок в явному вигляді фігурував в стовпці, що характеризує праві частини всіх рівнянь моделі. Для цього

з відповідних обмежень задачі базисні (у нашому випадку – штучні) змінні виражаються через небазисні: , ;

вирази для штучних змінних підставляються в ЦФ :

,

,

.

Відповідна симплекс-таблиця:

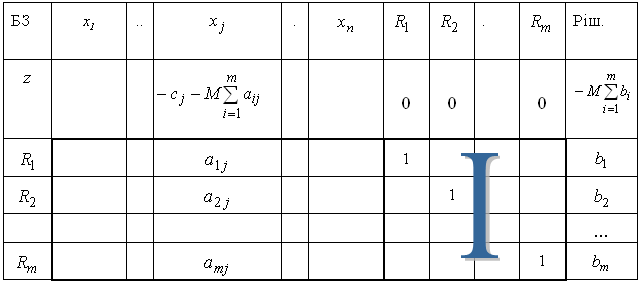
Якщо початкова задача – задача на мінімум, то при штучних змінних в - рядку усі коефіцієнти будуть мати протилежний знак:

Приклад

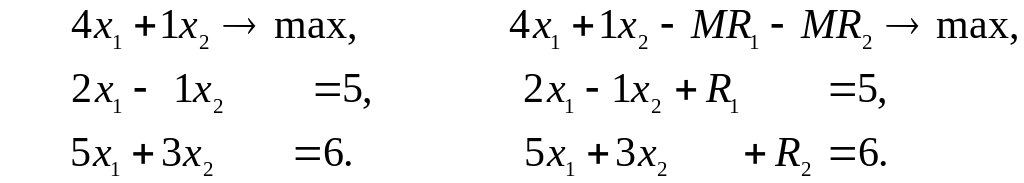
Початкова симплекс-таблиця:

Базисні змінні					Розв’язок
	-4-7	-1-2	0	0	-11
	2	-1	1	0	5
	5	3	0	1	6

-рядок симплекс-таблиці:

Нехай М=1000000. Тоді коефіцієнти в -рівнянні прикладу, що розглядається нами, такі:

(– 4 – 7000000) і (– 1 – 2000000).