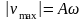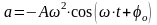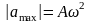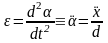- •45. Энергия витка с постоянным током во внешнем однородном магнитном поле.
- •46. Магнитный поток через замкнутую поверхность. Вихревой характер магнитного поля.
- •47. Общее выражение работы, совершаемой в магнитном поле над контуром с током.
- •48. Закон Фарадея для электромагнитной индукции. Правило Ленца.
- •49. Выражение эдс индукции, возникающей в проводнике, движущемся в магнитном поле.
- •50. Явление самоиндукции. Эдс самоиндукции. Индуктивность контура с током.
- •51. Получите выражение для индуктивности длинного соленоида.
- •52. Характеристики магнитного поля в веществе – магнитная индукция ,напряженность магнитного поля, намагниченность. Связь между ними.
- •1. Понятие магнитного момента атома.
- •53. Магнитная проницаемость и магнитная восприимчивость. Их определения и связь между ними.
- •56. Ферромагнетики, их основные свойства. Гистерезис. Применение ферромагнетиков.
- •55. Пара- и даимагнетики, их магнитные свойства. Поведение Диамангнетиков парамагнетиков в неоднородном магнитном поле.
- •57. Вихревое электрическое поле. Первое уравнение Максвелла в интегральной форме.
- •58. Максвелловская гипотеза о токах смещения . Второе уравнение Максвелла в интегральной форме.
- •59. Система уравнений Максвелла в интегральной форме с использованием векторов магнитной индукции и напряженности электрического поля.
- •60. Система уравнений Максвелла в интегральной форме в веществе.
- •61. Дифференциальное уравнение свободных гармонических колебаний и его решение. Амплитуда, период, начальная фаза колебаний.
- •62. Скорость и ускорение при гармонических колебаниях. Максимальная скорость и максимальное ускорение.
- •63. Сложение одинаково направленных гармонических колебаний одинаковой частоты. Нахождение амплитуды суммарного колебания с помощью метода векторных диаграмм.
- •64. Пружинный маятник. Дифференциальное уравнение колебаний пружинного маятника. Период его малых колебаний.
- •65. Математический маятник. Дифференциальное уравнение колебаний математического маятника. Период его малых колебаний.
- •67. Кинетическая ,потенциальная и полная энергия гармонических колебаний.
- •68. Дифференциальное уравнение затухающих колебаний и его решение. График зависимости амплитуды от времени.
- •69. Период затухающих колебаний. Логарифмический декремент колебаний. Время релаксации. Апериодическое движение.
- •70. Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний. Установившиеся колебания.
- •7 2.Волновое движение. Продольные поперечные волны, примеры. Волновой фронт.
- •73. Уравнение плоской бегущей волны. Длина волны. Волновое число. Разность фаз двух точек волны.
- •74. Стоячие волны. Получите выражение для смещения в стоячей волне. Узлы и пучности. Условие стационарности стоячих волн.
- •76. Скорость электромагнитной волны в веществе. Показатель преломления. Закон преломления волны на границе двух сред.
- •77. Скорость электромагнитной волны в веществе. Показатель преломления. Полное внутреннее отражение . Оптические волноводы.
- •78. Связь характеристик электрического и магнитного поля в элетромагнитной волне.
- •79. Энергия, переносимая электромагнитной волной. Плотность потока энергии(вектор Пойтинга) Ее размерность.
- •80. Интерференция света. Когерентность световых волн. Интерференционное условие максимумов и минимумов.
- •81. Интерференция света. Когерентность световых волн. Получение интерференционной картины от двух точечных когерентных источников (опыт Юнга).
- •82. Получите выражение для координат интерференционных полос на экране в опыте юнга.
- •83. Интерференция в тонкой пленке с параллельными поверхностями(полосы равного наклона).Выражение для оптической разности хода в этом случае.
- •85. Дифракционная решетка. Примерная картина дифракции. Получите выражение для определения выражения положения главных максимумов в картине дифракции.
- •86. Дифракционная картина как спектральный прибор. Формула для определения числа щелей, необходимого для разрешения двух близких длин волн.
- •87. Поляризация света . Естественный и поляризованный свет. Поляризация при отражении от диэлектрика. Угол Брюстера.
- •88. Поляризация света. Естественный и поляризованный свет. Поляризация при прохождении света через кристаллы. Двойное лучепреломление. Поляризатор. Закон Малюса.
62. Скорость и ускорение при гармонических колебаниях. Максимальная скорость и максимальное ускорение.
|
смещение точки от положения равновесия |
Учитывая, что скорость v=dx/dt и ускорение а=dv/dt и F= k x, можно получить:
|
|
скорость колеблющейся точки и ее амплитуда (максимальное значение) |
|
|
ускорение колеблющейся точки и его амплитуда (максимальное значение) |
|
|
возвращающая сила |
63. Сложение одинаково направленных гармонических колебаний одинаковой частоты. Нахождение амплитуды суммарного колебания с помощью метода векторных диаграмм.
Пусть
точка одновременно участвует в двух
гармонических колебаниях одинакового
периода, направленных вдоль одной
прямой. Сложение колебаний будем
проводить методом векторных диаграмм
(рис. 2.2). Пусть колебания заданы уравнениями
![]() и
и
![]()
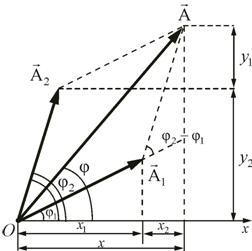
Отложим
из точки О вектор ![]() под
углом φ1 к
опорной линии и вектор
под
углом φ1 к
опорной линии и вектор
![]() под
углом φ2.
Оба вектора вращаются против часовой
стрелки с одинаковой угловой скоростью
ω, поэтому их разность фаз не зависит
от времени (
под
углом φ2.
Оба вектора вращаются против часовой
стрелки с одинаковой угловой скоростью
ω, поэтому их разность фаз не зависит
от времени ( ![]() ).
Такие колебания называют когерентными
).
Такие колебания называют когерентными
Нам
известно, что суммарная проекция
вектора ![]() равна
сумме проекций на эту же ось. Поэтому
результирующее колебание может быть
изображено вектором амплитуды
равна
сумме проекций на эту же ось. Поэтому
результирующее колебание может быть
изображено вектором амплитуды ![]() ,
вращающимся вокруг точки О с
той же угловой скоростью ω, что и
,
и
.
Результирующее колебание должно быть
также гармоническим с частотой ω:
,
вращающимся вокруг точки О с
той же угловой скоростью ω, что и
,
и
.
Результирующее колебание должно быть
также гармоническим с частотой ω:
![]()
По
правилу сложения векторов найдем
суммарную амплитуду:
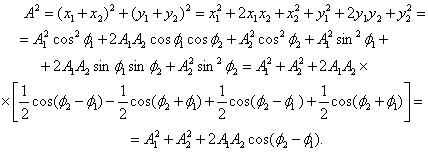
Результирующую
амплитуду найдем по формуле
![]() (*)
(*)
Начальная
фаза определяется из соотношения
![]()
Таким
образом, тело, участвуя в двух гармонических
колебаниях одного направления и
одинаковой частоты, совершает также
гармоническое колебание в том же
направлении и с той же частотой, что и
складываемые колебания. Из (*) следует,
что амплитуда А результирующего
колебания зависит от разности начальных
фаз ![]() .
Возможные значения А лежат
в диапазоне
.
Возможные значения А лежат
в диапазоне ![]() (амплитуда
не может быть отрицательной).
(амплитуда
не может быть отрицательной).
64. Пружинный маятник. Дифференциальное уравнение колебаний пружинного маятника. Период его малых колебаний.
Это система, состоящая из небольшого тела, подвешенного на легкой пружине и совершающего вертикальные колебания.
|
|
II закон Ньютона, сравнивая с (), найдем циклическую частоту и период колебаний |
|
В данном случае возвращающая сила – это упругая сила электромагнитной природы, т.е. сила , обусловленная взаимодействием молекул пружины. Выражения для смещения, скорости, ускорения тела – см. ранее. |
|||
65. Математический маятник. Дифференциальное уравнение колебаний математического маятника. Период его малых колебаний.
Это тело, подвешенное на легкой нити, размерами которого можно пренебречь по сравнению с длиной нити. Запишем II закон Ньютона в проекции на касательное к траектории (окружности) направление:
ma = mg sin , a тангенциальное ускорение. Это уравнение является уравнением колебаний, но не гармонических и имеет более сложно решение, чем (). Мы рассмотрим только случай малых углов . При малых углах
sin х / l, где l – длина нити.
|
|
II закон Ньютона; сравнивая с (), найдем циклическую частоту и период колебаний |
|
В данном случае возвращающая сила – это составляющая силы тяжести, т.е. |
|||
сила гравитационной природы, а т.к. при малых углах она пропорциональна смещению, ее можно назвать квазиупругой.
66. Физический маятник. Дифференциальное уравнение колебаний физического маятника. Период его малых колебаний.
Это любое твердое тело, способное совершать колебания относительно неподвижной точки , не совпадающей с его центром тяжести. Если маятник отклонить от положения равновесия, то возникнет возвращающий момент, создаваемый составляющей силы тяжести mg sin и равный mg sin d, где d – плечо силы (см. рис.). Данное тело может совершать только вращательное движение, поэтому II закон Ньютона будет иметь вид:
I =-mgd, где I – момент инерции тела, а - угловое ускорение. Это уравнение колебаний, но не гармонических. Однако при малых углах оно приобретает вид (), т.е. дифференциального уравнении гармонических колебаний. При малых углах sin x/d
d – расстояние от точки подвеса до центра тяжести.
угловое ускорение |
II закон Ньютона |
|
круговая частота и период колебаний физического маятника |
|
|
уравнение гармонических колебаний |
|
||
|
приведенная длина физического маятника. Если взять нить длиной lприв и подвесить к ней небольшое тело, получим математический маятник, период колебаний которого будет равен периоду колебаний физического маятника. |