51. Получите выражение для индуктивности длинного соленоида.

	индукция магнитного поля внутри соленоида
	магнитный поток через каждый из витков соленоида
	полный магнитный поток через все витки
	так как , получим выражение для индуктивности
	индуктивность длинного соленоида n- число витков на единицу длины соленоида l,S, V- длина, площадь сечения и объем соленоида

52. Характеристики магнитного поля в веществе – магнитная индукция ,напряженность магнитного поля, намагниченность. Связь между ними.

1. Понятие магнитного момента атома.

магнитного момента

	орбитальный магнитный момент электрона: Учитывая, что направление тока противоположно скорости электрона как отрицательно заряженной частицы орбитальный магнитный момент электрона на рис. 24.1 направлен вверх по правилу буравчика.

Заметим, что кроме орбитального магнитного момента, электрон обладает собственным (спиновым) магнитным моментом. Магнитный момент атома равен векторной сумме этих магнитных моментов.

Намагниченность.

Под воздействием магнитного поля всякое вещество способно приобретать магнитный момент (намагничиваться), т.е. является магнетиком. Намагниченное вещество создает магнитное поле , которое накладывается на внешнее поле . Оба поля в сумме дают результирующее поле .

Степень намагничивания магнетика характеризуется магнитным моментом единицы объема. Эту величину называют намагниченность

где – магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заключенным в объеме – физически бесконечно малом объеме в окрестности данной точки (но много больше объема молекулы); - средний магнитный момент одного молекулярного тока, - их концентрация.

Намагниченность принято связывать не с магнитной индукцией, а с напряженностью магнитного поля .Ограничимся пока рассмотрением магнетиков, для которых зависимость между и имеет линейный характер: (*)

где - магнитная восприимчивость, безразмерная величина, характерная для каждого данного магнетика.

В отличие от диэлектрической восприимчивости æ, которая всегда положительна, магнитная восприимчивость бывает как положительной, так и отрицательной. Соответственно магнетики, подчиняющиеся зависимости (*) подразделяются на парамагнетики ( ) и диамагнетики ( ). У парамагнетиков , у диамагнетиков . Кроме этих магнетиков существуют ферромагнетики, у которых зависимость имеет весьма сложный нелинейный характер (подробнее о магнетиках далее в п. 4).

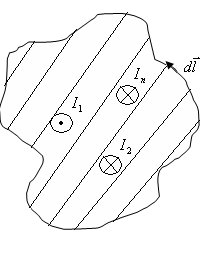
Закон полного тока для магнитного поля в веществе. Напряженность магнитного поля.

Постановка задачи. В пространство, окружающее макротоки , … (рис. 24.2) вносим различного рода магнетики, которые в поле токов ,… будучи намагничиваться. Найдем связь напряженности магнитного поля с токами. Предварительно свяжем намагниченность с молекулярными токами. Обозначим алгебраическую сумму макротоков , алгебраическую сумму микротоков .

Рассмотрим элемент контура . Токи молекул справа (вне контура) не пронизывают контур. Слева (внутри контура) пронизывают контур дважды и вклад в алгебраическую сумму токов равен нулю.

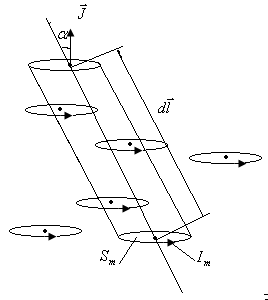
Дают вклад только те токи, которые «нанизаны» на контур. Элемент контура , образующий с направлением намагниченности угол , нанизывает на себя те молекулярные токи, центры которых попадают внутрь косого цилиндра с объемом ( – площадь, охватываемая отдельным молекулярным током, – высота косого цилиндра). Обозначим через концентрацию токов в единице объема. Сумма молекулярных токов в элементарном объеме :

.

Произведение равно магнитному моменту отдельного молекулярного тока , в свою очередь , следовательно: (по определению скалярного произведения). Проинтегрируем по контуру :

Циркуляция вектора по контуру равна алгебраической сумме молекулярных токов , натянутых на этот контур.

Закон полного тока с учетом токов проводимости и молекулярных токов: , где – алгебраическая сумма макротоков (знак «+» или «-» берется в соответствии с правилом правого винта по отношению к направлению обхода контура).

Раскроем скобки и заменим на :

Поделив обе части на и перенося в левую часть, получим: .

Обозначим

где – напряженность магнитного поля. С учетом введенного понятия напряженности получаем теорему о циркуляции вектора (закон полного тока для магнитного поля в веществе):

Циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макротоков, охватываемых этим контуром.

Магнитная проницаемость среды (54.Циркуляция вектора напряженности). Индукция магнитного поля в веществе.

В выражении заменим на , получим: ,

отсюда: .Обозначим – относительная магнитная проницаемость или просто магнитная проницаемость вещества, тогда:

То есть напряженность поля есть вектор, имеющий то же направление, что и вектор (для изотропных сред), но в раз меньший по модулю.

В случаях, когда однородный магнетик заполняет весь объем, ограниченный поверхностями, которые образованы линиями вектора (поле тока проводимости) [1].

Тогда ,

Магнитная индукция внутри магнетика будет в раз отличаться от .

Например, поле внутри соленоида при отсутствии магнетика . Если магнетик заполняет все пространство соленоида, где поле отлично от нуля (краевыми эффектами мы пренебрегаем), то магнитная индукция должна быть в раз больше:

В этом примере с соленоидом показывает, во сколько раз магнитная индукция поля образованного намагничивающим током в данном веществе, отличается от индукции поля, образованного этим же током в вакууме .