85. Дифракционная решетка. Примерная картина дифракции. Получите выражение для определения выражения положения главных максимумов в картине дифракции.
Дифракционная решётка – пространственная периодическая структура, период которой соизмерим с длиной световой волны. Различают пропускательные, отражательные, амплитудные и фазовые решетки. Пропускательные решетки работают на пропускание света, отражательные – на отражение. Амплитудные решетки пространственно модулируют амплитуду, фазовые - фазу световой волны. Простейшая амплитудная пропускательная решетка представляет собой систему равноотстоящих параллельных щелей в непрозрачном экране. Ширину щели обозначим b, а ширину непрозрачных промежутков между щелями – а. Величина d=a+b называется периодом или постоянной дифракционной решетки.
Отражательную амплитудную решетку изготавливают путем нанесения штрихов на плоское или вогнутое зеркало.
Общая ширина решетки l, число щелей N и постоянная решетки d связаны равенством l =Nd
Если известно число штрихов (N), приходящихся на 1 мм решѐтки, то период решѐтки находят по формуле: d = 1 / N мм.
Рассмотрим дифракцию плоской световой волны на периодической системе щелей в непрозрачном экране. В соответствии с принципом Гюйгенса–Френеля каждая щель решетки является источником вторичных волн. Разность хода между волнами, испускаемыми соседними щелями Δ=dsinφ. Условие главных максимумов принимает вид
Δ=
dsinφ=m
,
m=0,±1, ±2… (4)
где m – порядок дифракционного максимума.
Максимум нулевого порядка наблюдается при φ=0, первого порядка при sinφ=+- /d, второго порядка при sinφ=+-2 /d .
Главные минимумы соответствуют таким углам φ, в направлении которых ни одна из щелей не распространяет свет, поэтому условие главных минимумов, как и при дифракции на одной щели, выражает формула bsinφ=m , m=±1, ±2,±3…
дифракционная
картина
86. Дифракционная картина как спектральный прибор. Формула для определения числа щелей, необходимого для разрешения двух близких длин волн.
Кроме главных, имеется большое число слабых побочных максимумов, разделенных дополнительными минимумами. Положение главных максимумов (кроме центрального) зависит от длины волны . Поэтому при пропускании через решетку белого света все максимумы ненулевого порядка разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, а красный – наружу. Эта задача является актуальной для спектрального анализа, поскольку дифракционные решетки позволяют пространственно разделить лучи с разными длинами волн, и именно по отклонению луча в дифракционной решетке определяется длина волны света в решеточных спектрометрах. Таким образом, дифракционная решетка представляет собой спектральный прибор.
Разрешающая
сила дифракционной решетки:
,
где δλ – наименьшая разность длин волн двух близких спектральных линий, воспринимаемых при наблюдении раздельно, m – порядок спектра, N – общее число щелей дифракционной решетки.
87. Поляризация света . Естественный и поляризованный свет. Поляризация при отражении от диэлектрика. Угол Брюстера.
Для электромагнитных волн поляризация — явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H.
В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга. Свет, в котором направления колебаний упорядочены каким-либо образом, называется поляризованным.
Обозначим через ΘБр угол, удовлетворяющий условию tgΘБр = n12 (3) ,где n12 — показатель преломления второй среды относительно первой. При угле падения J1, равном ΘБр, отраженный луч полностью поляризован (он содержит только колебания, перпендикулярные к плоскости падения). Степень поляризации преломленного луча при угле падения, равном ΘБр, достигает наибольшего значения, однако этот луч остается поляризованным только частично.
Соотношение (3) носит название закона Брюстера, а угол ΘБр это Угол Брюстера.
Закон Брюстера — закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко убедиться в том, что при падении света подуглом Брюстера отраженный и преломленный лучи взаимно перпендикулярны, т.е.
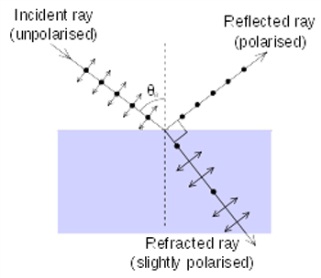
Угол Брюстера. Иллюстрация поляризации отражённого света, падающего на границу раздела сред под углом Брюстера.