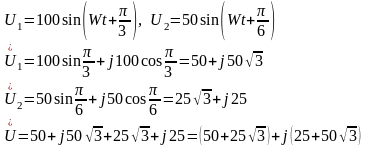- •1.Элементы электрических цепей.
- •2.Источники электрической энергии.
- •3)Топологические понятия теории эл. Цепей.
- •5. Основные принципы и св-ва эл. Цепей.
- •6.Эквивалентные преобразования пассивных участков электрических цепей.
- •7. Метод контурных токов.
- •8. Режимы работы активного двухполюсника.
- •9.Метод эквивалентного активного двухполюсника.
- •10. Метод двухузлов.
- •11.Понятие о четырехполюсниках. Коэффициент передачи.
- •12. Расщепление источников.
- •13.Однофазные цепи синусоидального тока. Основные понятия.
- •14.Изображение синусоидальной функции времени радиус-векторами в декартовой плоскости координат.
- •15.Комплексное изображение синусоидальных функций времени.
- •16.Электрическая цепь с (r) активным элементом.
- •17. Электрическая цепь индуктивным (l)-элементом.
- •18. Электрическая цепь с ёмкостным элементом
- •19. Последовательное соединение элементов в цепи синусоидального тока.
- •20. Построение векторных диаграмм при последовательном соединении
- •21. Параллельное соединение элементов в цепи синусоидного тока.
- •22. Построение векторных диаграмм для // соединения
- •23. Частотные св-ва цепей синусоидального тока.
- •24. Мощность цепи переменного тока.
- •25. Технико-экономическое значение повышения коэф-та мощности.
- •26. 3Х фазные электрические цепи.
- •27. Способы соединения фаз 3х фазного источника питания.
- •28. Соединение элементов 3х фазной цепи звездой.
- •29. Соединение элементов 3х фазной цепи треугольником.
- •30. Активная, реактивная полная мощность в трёхфазных приёмников (симметричных).
- •31.Электрические аппараты
- •32,33,34. Трансформаторы. 3х фазные трансформаторы. Аввтотрансформаторы. Измерительные трансформаторы.
- •35. 1. Устройство электрической машины постоянного тока
- •36. Электрические машины постоянного тока. Двигатель постоянного тока.
- •37. 3Х фазный асинхронный генератор.
- •38. Синхронный двигатель
14.Изображение синусоидальной функции времени радиус-векторами в декартовой плоскости координат.
Электрическое состояние цепей переменного тока так же как и цепей постоянного тока описывается уравнениями Киргофа, Поэтому любую электрич. цепь переменного тока можно рассчитать используя з-ныКиргофа и применяя действующее значение электр. величины. Однако решать т.о. достаточно грамозко. Для упрощения решения можно использовать графические мет-ды. Для этого, представим радиус-вектор длиной Ам, вращающейся в декартовой пл-стиху против часовой стрелки, с частотой W и периодом Т. Тогда, проекция вращающегося вектора на ось у будет записываться след-им образом.
 .
.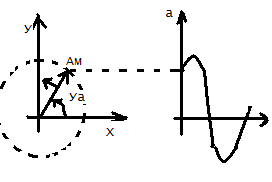 Любой ток можно представить как
радиус-вектор. Т.о.равномерно вращающейся
радиус-вектор однозначно соответствует
некоторой синусоидальной функции
(например току или напряжению).
Любой ток можно представить как
радиус-вектор. Т.о.равномерно вращающейся
радиус-вектор однозначно соответствует
некоторой синусоидальной функции
(например току или напряжению). .
.
.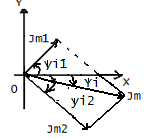
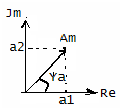
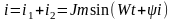 Такая совокупность векторов наз-ся
векторной диаграммой и применение
такого метода можно использовать для
сложения(вычитания) любого коли-ва
синусоид-ых функций, но только одинаковой
частоты. Недостатком такого метода,
явл. ограниченность точности.
Такая совокупность векторов наз-ся
векторной диаграммой и применение
такого метода можно использовать для
сложения(вычитания) любого коли-ва
синусоид-ых функций, но только одинаковой
частоты. Недостатком такого метода,
явл. ограниченность точности.
15.Комплексное изображение синусоидальных функций времени.
Комплексные изображения позволяют совместить простоту и наглядность векторных диаграмм с возможностью проведения точных аналитических расчетов. Для этого перенесём радиус-вектор на комплексную плоскость, совместив ось ОХ с осью действительных чисел, а ОУ-мнимых.

 .
Существует несколько форм записи
комплексного числа: 1.алгебраическая
.
Существует несколько форм записи
комплексного числа: 1.алгебраическая ,
где
,
где
 -комплексное
число,
-комплексное
число,
 -мнимая
единица(
=
-мнимая
единица(
= ).
2.триганометрическая
).
2.триганометрическая
 ,
где
,
где
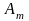 -длина
радиус-вектора. 3.показательная
-длина
радиус-вектора. 3.показательная
 .
При «+» комплексных чисел удобно
использовать алгебраическую форму
записи. При
.
При «+» комплексных чисел удобно
использовать алгебраическую форму
записи. При
 -показательную.
Для перехода из одной формы записи в
другую используют форм-лы (1). В комплексных
числах используют след. обозначения:
-модуль
компл-ого числа,
-показательную.
Для перехода из одной формы записи в
другую используют форм-лы (1). В комплексных
числах используют след. обозначения:
-модуль
компл-ого числа,
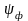 -аргумент
компл-ого числа. Для единичных действующих
и мнимых чисел выполняется след.соотношения
(единичным наз. такое число у которого
модуль =1, (
=1)):
-аргумент
компл-ого числа. Для единичных действующих
и мнимых чисел выполняется след.соотношения
(единичным наз. такое число у которого
модуль =1, (
=1)):
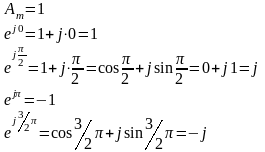
Д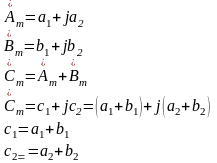 ля
«+» комплексных чисел их представляют
в алгебр-кой форме записи:
ля
«+» комплексных чисел их представляют
в алгебр-кой форме записи:
Аналогично проводится и для «-». Для комплексные числа записываются в показательной форме записи:
 .
.
При
изображении синусоидальной функции
комплексным числом, модуль комплексного
числа есть амплитуда, а аргумент –
начальная фаза.Изображение вектора на
комплексной плоскости и соответ-щие им
комплексные числа обозначают той же
буквой, что и амплитуда, но с точкой на
верху. Пример: Найти комплексное изоб-ние
напряжения в показательной, алгебраической
и тригонометрической форме записи, если
известно, что мгновенное значение
напряжения измен-ся по след-му закону
 .
.
Такое
комплексное число (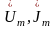 )
наз. комплексной амплитудой, т.к. его
модуль = амплитуде изображаемой синусойды.
Помимо комплексных амплитуд в электрот-ке
используют понятие комплексного
действующего тока и напряжения, кот.наз.
комплексное напряжение и комплексный
ток, и обозначается след. образом:
)
наз. комплексной амплитудой, т.к. его
модуль = амплитуде изображаемой синусойды.
Помимо комплексных амплитуд в электрот-ке
используют понятие комплексного
действующего тока и напряжения, кот.наз.
комплексное напряжение и комплексный
ток, и обозначается след. образом:
 .
Пример: Определить чему будет = суммарное
напряжение
.
Пример: Определить чему будет = суммарное
напряжение
 .
.