(6.) геометрическая или лучевая оптика, в основе которой лежит представление о световых лучах; Основные законы геометрической оптики: 1)закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет.

2) Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.

3) Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред: .Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.

Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления: n = n2 / n1.

При переходе света из оптически более плотной среды в оптически менее плотную n2 < n1 (например, из стекла в воздух) можно наблюдать явление полного отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол αпр, который называется предельным углом полного внутреннего отражения

Для угла падения α = αпр sin β = 1; значение sin αпр = n2 / n1 < 1.

(7.) Простейшим оптическим устройством, способным создавать изображение предмета, является плоское зеркало. Изображение предмета, даваемое плоским зеркалом, формируется за счет лучей, отраженных от зеркальной поверхности. Это изображение является мнимым, так как оно образуется пересечением не самих отраженных лучей, а их продолжений в «зазеркалье» (рис 3.2.1). Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента. Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.

Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом F зеркала. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала (рис 3.2.2). Положение изображения и его размер можно также определить с помощью формулы сферического зеркала:

Здесь d – расстояние от предмета до зеркала, f – расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:

d > 0 и f > 0 – для действительных предметов и изображений;

d < 0 и f < 0 – для мнимых предметов и изображений.

(10.) Разрешающая способность (в оптике) Вследствие дифракции света на краях оптических деталей даже в идеальной оптической системе (т. е. безаберрационной; см. Аберрации оптических систем) изображение точки есть не точка, а кружок с центральным светлым пятном, окруженным кольцами (попеременно тёмными и светлыми в монохроматическом свете, радужно окрашенными - в белом свете). Теория дифракции позволяет вычислить наименьшее расстояние, разрешаемое системой, если известно, при каких распределениях освещённости приёмник (глаз, фотослой) воспринимает изображения раздельно. Согласно Рэлею (1879), изображения двух точек одинаковой яркости ещё можно видеть раздельно, если центр дифракционного пятна каждого из них пересекается краем 1-го тёмного кольца другого (рис.). В случае самосветящихся точек, испускающих некогерентные лучи, при выполнении этого критерия Рэлея наименьшая освещённость между изображениями разрешаемых точек составит 74% своего максимального значения, а угловое расстояние между центрами дифракционных пятен (максимумами освещённости) Dj = 1,21 lID, где l - длина волны света, D - диаметр входного зрачка оптической системы (см. Диафрагма в оптике). Если f - фокусное расстояние оптической системы, то линейная величина рэлеевского предела разрешения s = 1,21 lflD.

(8.) Центрированная оптическая система – это оптическая система, которая имеет ось симметрии (оптическую ось) и сохраняет все свои свойства при вращении вокруг этой оси.

Для центрированной оптической системы должны выполняться следующие условия:

все плоские поверхности перпендикулярны оси,

центры всех сферических поверхностей принадлежат оси,

все диафрагмы круглые, центры всех диафрагм принадлежат оси,

все среды либо однородны, либо распределение показателя преломления симметрично относительно оси.

Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.

Линзы входят в состав практически всех оптических приборов. Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше (рис. 3.3.1).

Рисунок 3.3.1.

Собирающие (a) и рассеивающие (b) линзы и их условные обозначения

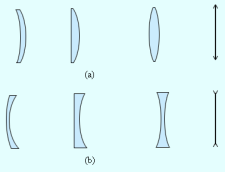
Прямая, проходящая через центры кривизны O1 и O2 сферических поверхностей, называется главной оптической осью линзы. В случае тонких линз приближенно можно считать, что главная оптическая Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:

Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единицой измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = м–1.

Формула тонкой линзы аналогична формуле сферического зеркала.

Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0.

( 9.) оптических систем. В определении понятия изображения содержится требование того, чтобы все лучи, выходящие из точки предмета, сходились в одной и той же точке в плоскости изображения, при этом увеличение для всех точек предмета остается постоянным. Отклонения фактически получаемого изображения от идеального, описываемого всеми предыдущими формулами, называются аберрациями. Для параксиальных лучей аберрации малы и ими пренебрегают. Если же лучи не параксиальны, то аберрации становятся значительными и сильно искажают изображение.

Первый источник аберраций состоит в том, что линзы, ограниченные сферическими поверхностями, преломляют лучи не совсем так, как это принимается в параксиальном приближении (например, фокусы для лучей, падающих на разных расстояниях от оси линзы, различны.). Такие аберрации называются геометрическими. Например, параксиальное приближение основывается на линейном разложении синуса в ряд. Неучтенные в таком приближении члены ~a³, ~a⁵ и т.д. приводят к аберрациям третьего, пятого и т.д. порядков.К геометрическим аберрациям относятся:

1. Сферическая аберрация.

2. Кома.

3. Астигматизм.

4. Искривление поверхности изображения (кривизна поля).

5. Дисторсия.

При сферической аберрации лучи, параллельные оптической оси, не пересекаются после линзы в одной точке. Пучок параллельных оси лучей после преломления образует совокупность конусов, вершины которых расположены на оси. Огибающая эту совокупность конусов поверхность называется каустической, а сечение этой поверхности любой плоскостью, проходящей через луч – каустической кривой (рис.).

Если светящаяся точка расположена не на оптической оси, то её изображение не является светящимся кружком, как в предыдущем случае, а представляется в виде довольно сложной асимметричной фигуры, напоминающей комету с хвостом. Такая аберрация называется комой.

Если на линзу падает цилиндрический пучок лучей под достаточно большим углом к оптической оси, то в результате сечение пучка лучей изменяется с расстоянием от линзы после преломления (рис.5.7). На некотором расстоянии от линзы сечение является отрезком линии, перпендикулярным плоскости падения пучка (такая плоскость падения, образованная осью падения пучка и оптической осью, называется меридианальной плоскостью, а перпендикулярная ей – сагиттальной). Затем эта линия переходит в эллипс, на некотором расстоянии дальше сечение опять становится круговым, а затем эллиптическим и дальше превращается в отрезок линии, лежащей в меридианальной плоскости. Такой вид аберрации называется астигматизмом.

Поверхности, на которых лежат фокусы (где образуются отрезки линий при астигматизме), создаваемые меридианальной и сагиттальной фокусировками, не совпадают между собой и не являются плоскостями. Эти поверхности касаются лишь в точке F^/ оптической оси. Этот вид аберрации называется искривлением поверхности изображения.

Увеличение системы, вообще говоря, зависит от угла наклона падающих лучей. В результате, например, сетка из прямых линий превращается в сетку из кривых линий. Такая аберрация называется дисторсией (рис.5.8).

Второй источник аберраций связан с дисперсией света. Т.к. показатель преломления зависит от частоты, то и фокусное расстояние и другие характеристики системы зависят от частоты. Поэтому лучи, соответствующие излучению различной частоты, исходящие из одной точки предмета, не сходятся в одной точке изображения даже в идеальном случае. Такие аберрации называются хроматическими.

(11.) 1. Глаз. (рис.5.9)

Ф окусировка глаза на предмет называется аккомодацией. Средние характеристики человеческого глаза:

Оптическая сила ~ 58 дптр.

Длина глаза ~ 22 мм.

Радиус кривизны сетчатки ~ 9,7 мм;

преломляющей оверхности ~ 5,6 мм.

Показатель преломления среды 1,33;

хрусталика ~ 1,4 – 1,45.

Расстояние наилучшего зрения 25 см.

2. Линзовый телескоп (рис.5.10). Увеличение (5.60)

3. Лупа . Простейшая оптическая система с малым фокусным расстоянием (~1 см или немного больше). Предмет располагается на расстоянии от лупы меньше фокусного. Изображение мнимое, прямое, увеличенное. Увеличение

(5.61)

г де D – расстояние наилучшего зрения (25 см).

4. Микроскоп. Передняя собирающая линза называется объективом (f₁ около сантиметра), задняя – окуляром (f₂ около нескольких сантиметров). Объектив строит увеличенное перевернутое действительное изображение, окуляр играет роль лупы для этого изображения как предмета. Увеличение

(5.62)

где d – расстояние между фокусами объектива и окуляра.

(12.) Под интерференцией света обычно понимают широкий круг явлений, в которых при наложении световых волн результирующая интенсивность не равна сумме интенсивностей отдельных волн: в одних местах она больше, в других – меньше, т.е. возникают чередующиеся светлые и темные участки – интерференционные полосы. Другими словами, интерференцией называется изменение средней плотности потока энергии, обусловленное суперпозицией электромагнитных волн. В дальнейшем под интенсивностью световой монохроматической волны будем понимать следующую величину, определяемую формулой: (6.1)

где E₀ – действительная амплитуда световой волны.

Принцип суперпозиции есть физическая гипотеза , согласно которой для световых волн возмущение , создающееся при прохождении ряда волн , равно алгебраической сумме возмущений , производимых каждой волной в отдельности. Уравнение (2.4.1) является математической формулировкой этого принципа .

Когерентные волны - волны когерентных источников.

Источники, у которых разность фаз остается постоянной, называются когерентными источниками.

Существуют различные способы создания когерентных источников. Наиболее простой способ создать когерентные источники — использовать реальный источник и его изображение. Основные схемы наблюдения интерференции в немонохроматическом свете используют деление волнового фронта (обычно от точечного источника) или деление амплитуды волны. При этом создаются две когерентных волны, которые интерферируют при небольшой разности хода.

Реальные источники практически не могут быть когерентными.

(13.) Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра.

Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рис. 3.7.2).

Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга

онохроматическая (или синусоидальная) волна, распространяющаяся в направлении радиус-вектора , записывается в виде E = a cos (ωt – kr),

где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ: E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ).

Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2.

Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:

(*)

где Δ = r2 – r1 – так называемая разность хода.

Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2, ...). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивности Imin = (a1 – a2)2 < I1 + I2. На рис. 3.7.4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.

В частности, если I1 = I2 = I0, т. е. интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид: I = 2I₀(1 + cos

kΔ).

В этом случае Imax = 4I₀, Imin = 0.

Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты.

Если в схеме Юнга через y обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда d << L и y << L (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить:

При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl, т. е. при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно, где ψ – угол схождения «лучей» в точке наблюдения P.

14.

15.

(16.) Определим контрастность интерференционной картины.

Наличие экрана повышает контрастность интерференционной картины, что позволяет увеличить яркость восстановленного изображения.

Это усовершенствование позволяет сохранить контрастность интерференционной картины и возможность точных отсчетов на всем диапазоне шкалы компенсатора вплоть до предельных углов наклона его пластинки. Существенным является также и вопрос о коэффициенте отражения света от поверхностей пластинки. Контрастность интерференционной картины определяется соотношением между интенсивностями интерферирующих пучков. Наиболее контрастной картина получается в том случае, когда интенсивности когерентных пучков одинаковы. Избыток энергии в одном из них создает вредный светлый фон. В настоящее время имеется возможность изменять коэффициент отражения в очень широких пределах путем нанесения металлических пленок на отражающие поверхности.

Освещенность пропорциональна интенсивности / падающего света. Количественной характеристикой контрастности интерференционной картины служит безразмерная величина видимость поло.

При значительных разностях хода светлые волосы одной составной части спектра белого света будут накладываться на темные полосы другой его части, имеющей другую длину волнь. В результате этого контрастность интерференционной картины будет падать до нуля и дальнейшие полосы уже не будут видны.

17.

18.

(19.) Интерференция в тонких пленках. При распространении световой волны в среде уменьшается скорость распространения волны и соответственно ее длина волны, т.к. ее частота не изменяется. При расчете изменения фаз волны в среде в качестве длины пути удобнее брать оптическую длину пути, равную геометрической длине, умноженной на показатель преломления:

. (6.28)

Тогда длину волны и волновой вектор в формулах можно задавать равными их значениям в вакууме.

а) Полосы равного наклона. Рассмотрим случай, когда плоская монохроматическая волна падает под углом j на поверхность плоскопараллельной пластинки с относительным показателем преломления n и толщиной h (рис.6.7). Интерференция возникает между двумя волнами, отраженными от верхней и нижней поверхностями пластины. Так как эти пучки параллельны между собой, то интерференция наблюдается (локализована) или на бесконечности или в фокальной плоскости F линзы Л. С учетом потери полволны на границе раздела сред (если n > 1, то в точке A, если n < 1, то в точке B) оптическая разность хода в данном случае равна . (6.29)

Из геометрии рисунка (вывести самостоятельно !) получаем для оптической разности хода: . (6.30)

Условием максимума интерференционной картины по-прежнему является

. (6.31)

а условием минимума –

(6.32)

Если на пластинку падают непараллельные пучки света, то и интерферирующие пучки будут иметь всевозможные направления распространения. При заданных толщине пластины и показателе преломления каждому углу падения волны соответствует своя интерференционная полоса. Поэтому такие полосы и называют полосами равного наклона. Если падающий свет не монохроматичный, при увеличении разности длин падающих волн интерференционные кольца разделяются и при некотором значении этой разности полосы соседних порядков перекрываются. Разность длин волн, при которой наступает перекрытие полос соседних порядков интерференции, называется дисперсионной областью (или областью свободной дисперсии).

б ) Полосы равной толщины. Теперь рассмотрим интерференцию света на пластинке с переменной толщиной (клине) (рис.6.8). Интерференционную картину можно также наблюдать и с помощью линзы на экране. В этом случае поверхность проецируется на экран наблюдения. Линии одинаковой интенсивности совпадают с линиями постоянной толщины пластины, поэтому соответствующие интерференционные полосы называются полосами равной толщины. Ограничения на толщину клиновидной пластины, связанные со степенью когерентности (или монохроматичности) такие же, как и в случае плоскопараллельной пластины.

(20.) Просветление оптики. Во многих современных оптических системах используются многочисленные оптические детали (линзы, призмы и др.), отражение от которых ослабляют интенсивность прошедшего света. Поэтому сведение к минимуму френелевских (т.е. рассчитываемых по формулам Френеля) потерь (просветление оптики) становится важной задачей. Явление интерференции позволяет сделать это достаточно эффективно. Для этого на поверхность оптического элемента наносят тонкий слой вещества (пленку), в которой и происходит интерференция (рис.6.14). Пусть n₁ – коэффициент преломления внешней среды, из которой падает свет, n₂ , h – соответственно коэффициент преломления и оптическая толщина пленки, n₃ – коэффициент преломления оптического элемента. Если рассмотреть только двухлучевую интерференцию между волнами 1 и 2, то для полного гашения отраженных пучков, т.е. для полного просветления оптики, необходимо выполнение двух условий:

1) плитуды пучков должны быть равными;

2) разность фаз между ними должна равняться p (т.е. волны находятся в противофазе).

Первое условие достигается подбором показателя преломления пленки. Второе условие легко выполняется, если оптическая толщина пленки равна l/4.

Более точно и правильнее соотношение для показателя преломления пленки можно найти, рассмотрев аналогично интерферометру Фабри–Перо многолучевую интерференцию. Тогда для относительной интенсивности отраженного от такой системы света получаем:

, (6.54)

где – амплитудные коэффициенты отражения от первой и второй границ раздела соответственно, d – оптическая разность хода между двумя соседними интерферирующими волнами. Положив d=p, а падение – нормальным, получаем: . (6.55)Т.к. при нормальном падении света , то интенсивность отраженного света будет равна нулю, если

. (6.56)

Тогда окончательно получаем условие полного просветления (совместно с : . (6.57)Если первая среда – воздух, а третья – стекло, то удовлетворить этому соотношению весьма трудно, т.к. твердых веществ со столь малым коэффициентом преломления ( ) в оптическом преломления не существует. Существующие вещества типа виллиолента (NaF), криолита (Na₃AlF₆) (показатели преломления ) позволяют уменьшить коэффициент отражения до 0,8%. Дальнейшее уменьшение коэффициента отражения может быть достигнуто применением многослойных просветляющих покрытий.

21.

(22.) Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Принцип Гюйгенса–Френеля

Метод зон Френеля Френель предложил метод разбиения фронта волны на кольцевые зоны, который впоследствии получил название метод зон Френеля.

Пусть от источника света S распространяется монохроматическая сферическая волна, P - точка наблюдения. Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP.

Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на l/2 - половину длины световой волны. Это разбиение было предложено O. Френелем и зоны называют зонами Френеля.

Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна l/2. Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке P.

Из геометрических соображениях следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером m, уменьшается с ростом m, т.е.

(23.) Дифракция Френеля на круглом отверстии

Пусть на пути сферической световой волны, испускаемой источником S, расположен непрозрачный экран с круглым отверстием радиуса r0. Если отверстие открывает четное число зон Френеля, то в точке P будет наблюдаться минимум, так как все открытые зоны можно объединить в соседние пары, колебания которых в точке P приблизительно гасят друг друга.

При нечетном числе зон в точке P будет максимум, так как колебания одной зоны останутся не погашенными.

Можно показать, что радиус зоны Френеля с номером m при не очень больших m:

.

Расстояние "a" примерно равно расстоянию от источника до преграды, расстояние "b" - от преграды до точки наблюдения P.

Если отверстие оставляет открытым целое число зон Френеля, то, приравняв r₀ и r_m, получим формулу для подсчета числа открытых зон Френеля:

При m четном в точке P будет минимум интенсивности, при нечетном - максимум.

Зонная пластинка. Закроем все нечетные зоны, оставив открытыми четные (или наоборот). В результате получится пластинка, называемая зонной пластинкой. Из рис. 7.3 видно, что амплитуды поля в точке P будут определяться суммой сонаправленных векторов и т.д. Поэтому осуществляется интерференция волн с усилением. Следовательно, в точке P на оси происходит значительное усиление интенсивности света (примерно в m² большее, чем дает отверстие в одну зону), т.е. в этой точке свет фокусируется. Зонная пластинка ведет себя как линза. Найдем фокусное расстояние f такой линзы. Будем считать, что лучи падают на зонную пластинку параллельно оси системы, т.е. R = ¥. Тогда точка P является фокусом. Формула (7.5) примет вид:

Следовательно фокусное расстояние равно:

Формула такой линзы принимает вид:

В отличие от обычной линзы зонная пластинка имеет несколько фокусов на оси системы в зависимости от количества открытых зон. Отметим, что и расположение зон Френеля на волновом фронте зависит от геометрии рассматриваемой системы.

Интенсивность света в фокусе можно увеличить еще в 4 раза по сравнению с зонной пластинкой, если изменить на p фазы вторичных волн, исходящих от всех нечетных (или наоборот – четных) зон. Это можно сделать, например, химическим травлением стеклянной пластинки в нужных местах, чтобы ее толщина там уменьшилась на (n – 1)l/2. В этом случае вторичные волны от всех точек волновой поверхности приходят в точку фокуса в одинаковых фазах. Такая дифракционная линза называется линзой Френеля.

(24.) Дифракция на щели.

Рассмотрим падение плоской монохроматической световой волны на бесконечную щель шириной b (рис.7.9). Участок dx, находящийся на расстоянии x от левого края щели (начала координат), в направлении Z’ излучает плоскую волну с запаздыванием фазы относительно точки О на kx×Чsinj. Угол j отсчитывается от оси Z – нормали к щели (первоначального направления падающей волны), k – волновое число падающей волны. При записи амплитуды волны учтем, что вся щель в направлении j = 0 посылает излучение с амплитудой E₀. Предполагая равномерное распределение амплитуды по щели, получим, что участок dx щели пошлет в направлении Z’ волну dE₁ с амплитудой E₀dx/b :

(7.39)

Отсюда имеем для амплитуды волны от всей щели: (7.40)

После несложного интегрирования и перехода от поля к интенсивности, получаем интенсивность дифракционной картины: где I₀ = E₀² ; I₁ = E₁² ; . (7.42)

Проанализируем выражение (7.41). При j = 0 u =0. Используя соотношение , получаем, что в центре дифракционной картины интенсивность максимальна и равна I₀ .

2. При углах j, для которых sinu = 0, а u ¹ 0 интенсивность света обращается в нуль. Тогда условие минимума дифракционной картины на одиночной щели принимает вид: (7.43)

3. Основная часть потока энергии сосредоточена в пределах изменения угла дифракции j между первыми (n = ±1) симметричными максимумами. График зависимости (7.41) приведен на рис.7.10.

4. Чем меньше (уже) щель, тем шире центральный максимум. Нетрудно заметить, что при b » l центральный максимум расплывается на всю полуплоскость (j » p/2). Дальнейшее уменьшение щели приводит лишь к монотонному уменьшению интенсивности прошедшего света.

И зучение картины дифракции дает информацию о ширине щели, если известна длина волны используемого света. Наоборот, зная ширину щели, можно найти длину волны. Таким образом, дифракционная картина от данного объекта имеет характерный вид, позволяющий получать информацию о размерах этого объекта. Отмеченное обстоятельство носит достаточно общий характер и лежит в основе метрологического применения дифракционных явлений.

(25.) на круглом отверстии. Пусть R – радиус отверстия. Расчет удобнее вести в полярных координатах (r, q) и (r’, q’) в плоскостях отверстия и дифракционной картины:

(7.44)

Тогда (7.35) для этого случая запишется в виде:

(7.45)

где – функция Бесселя m-го порядка. Воспользуемся свойством функций Бесселя:

. (7.46)

Тогда получаем (рис.7.11):

. (7.47)

И нтенсивность дифракционной картины определяется квадратом этой функции, т.е. в центре картины имеется светлое круглое пятно, окруженное темными и светлыми кольцами. Максимумы интенсивности быстро убывают. Радиусы колец определяются из корней функции Бесселя J₁ (r)=0. Т.к. существует приближенное соотношение , то качественно распределение интенсивности выглядит примерно так же, как и на рис.7.10. Угловой размер центрального светлого пятна (диска Эйри), наблюдаемого из центра круглого отверстия, равен:

.

26.

( 27.) Дифракционная решетка. Прозрачная (амплитудная) дифракционная р ешетка представляет собой правильную плоскую структуру из большого количества параллельных щелей с шириной каждой щели b и расстоянием d между соседними щелями. Расстояние d чаще называют периодом или постоянной дифракционной решетки (рис.7.12). Пусть на эту решетку нормально падает плоская монохроматическая волна. Найдем интенсивность света I в дифракционной картине.

Методика расчета и система обозначений та же, что и для одиночной щели. От элемента dx какой-то n-й щели в исследуемом направлении распространяется волна вида:

(7.49)

Вся n-я щель пошлет волну вида: (7.50)Для учета действия всех щелей по принципу суперпозиции можно сложить все образовавшиеся напряженности поля: (7.51)

где N – полное число щелей, участвующих в дифракции. Множитель с интегралом был посчитан выше для случая одной щели. Он не зависит от n и может быть вынесен за знак суммы. Введем обозначение:

(7.52)Сумма в (7.51) представляет собой сумму N членов геометрической прогрессии. Тогда (7.51) перепишется в виде:

(7.53)

Интенсивность света в дифракционной картине получается умножением (7.53) на комплексно сопряженную величину I=EE^* :

(7.54)

Множитель (sinu/u)² характеризует распределение интенсивности в результате дифракции плоской волны на каждой щели и является огибающей всей дифракционной картины, а множитель (sinNd/sind)² учитывает интерференцию между волнами, исходящими от всех щелей. Множитель I₀ определяет интенсивность света, излучаемого в направлении j = 0, которая зависит от потока энергии, падающего на решетку света. Вид дифракционной картины показан на рис.7.13.

Величина dsinj равна разности хода между волнами, испускаемыми двумя эквивалентными точками соседних щелей. Условие главных максимумов для дифракционной решетки определяется формулой:

(7.55)

А условие (7.43) определяет положение минимумов огибающей. Наклонное падение света на дифракционную решетку. Пусть параллельный пучок света падает на дифракционную решетку под углом q (рис.7.14). Как и прежде дифракционные максимумы будут наблюдаться при разности хода волн, идущих от одинаковых точек соседних щелей, равной целому числу длин волн:

(7.56)

где j_m – направление на m-й максимум. При , как правило, углы дифракции малы, поэтому . (7.57)

Обозначив , а , получаем условие максимума . (7.58)Т.е., при наклонном падении света на решетку, если вести отсчет углов о падающих лучей, роль периода решетки играет проекция периода решетки на перпендикулярное падающему пуску направление. Это позволяет использовать решетки с большим периодом для дифракции с очень короткой длиной

28.

29.

(30.) Голографией называют метод записи и последующего восстановления пространственной структуры световых волн, основанный на явлениях интерференции и дифракции когерентных пучков света. Как и фотография, она обеспечивает возможность записи, хранения и воспроизведения зрительных образов предметов. Фотопластинка, на которой записана эта информация, называется голограммой.

(31.) Поляризация называется параллельной, если вектор электрического поля E лежит в плоскости падающего луча и нормали к границе раздела сред (см. рисунок ниже). В противном случае поляризация называется перпендикулярной.

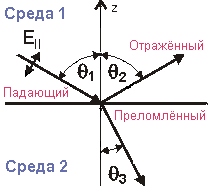
Согласно формуле Френеля угол падения луча q1, угол отражения q2 и угол преломления q3 связаны следующими уравнениями:

q₁ = q₂

n₁sinq₁ = n₂sinq₃

Отражательная способность границы раздела сред для лучей с параллельной и перпендикулярной поляризацией R|| и R^, а также пропускательная способность границы сред T|| и T^ описывается выражениями:

Для луча, падающего нормально к границе раздела, исчезает различие между перпендикулярной и параллельной компонентами, т.е.