1. Способ цепных подстановок как прием последовательного элиминирования. Его модификации.

Это основной способ. Для применения в анализе любого способа последовательного элиминирования необходимо выделить пять основных моментов:

1. Цель анализа (D - абсолютный результат).

2. Возможности применения (использования) соответствующего способа. Три основных подгруппы (возможности) применения того или иного способа:

-       можно использовать;

-       нельзя использовать;

-       можно, но нецелесообразно.

Здесь имеется ввиду тип формулы.

Прием ЦП используется при любом типе зависимости, кроме обратной аддитивной.

3.     Информационное обеспечение (данные) – ее вид или характер и полнота (в единицах измерения, или в процентах, т.е. в абсолютных или относительных показателях).

4.   Суть алгоритма анализа (набор арифметических, логических действий).

5.     Аналитическая проверка. Существует три варианта.

Допустим, дана сложная мультипликативная зависимость, выраженная системой уравнений :

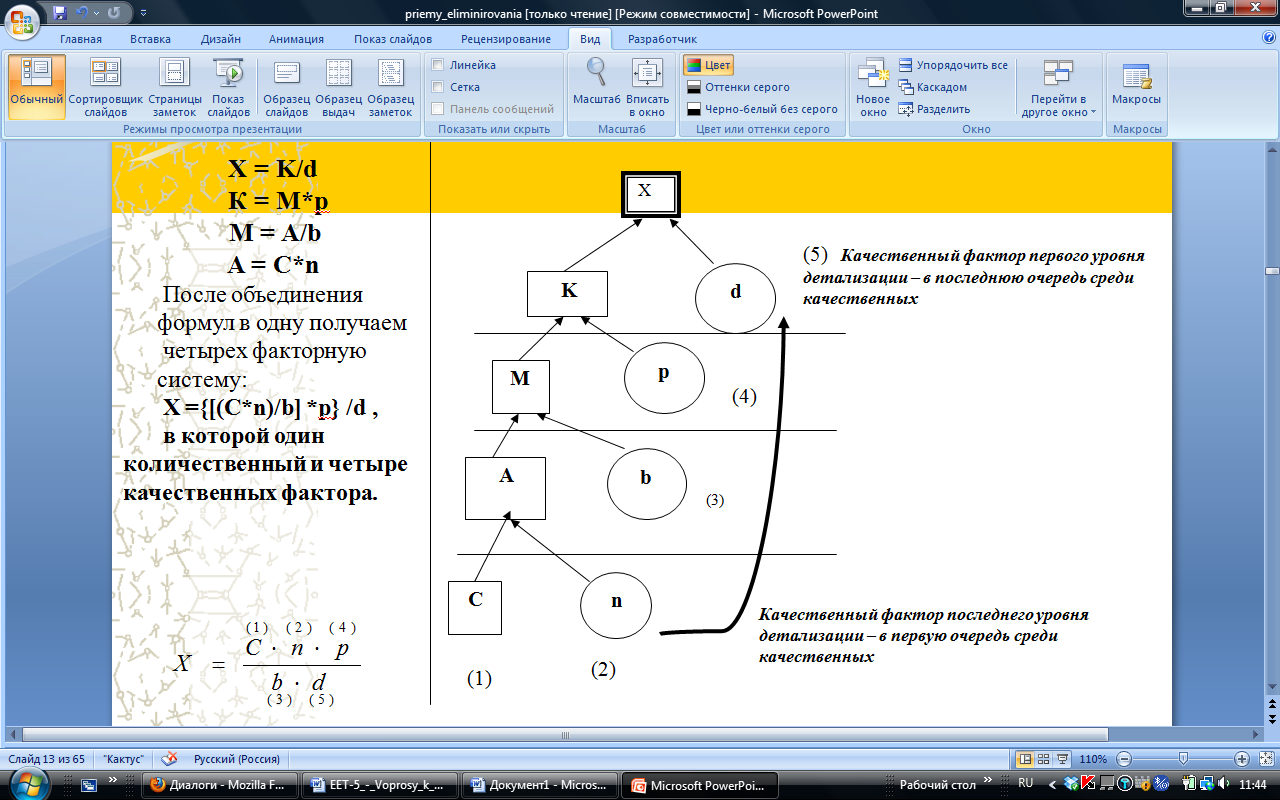
Информационная база:

В нашем примере:

[n] = 5 – это число первичных факторов;

[1] = результативный показатель;

[n+1] = 6 - общее число параметров факторной системы;

[n+1] = 6 – общее число подстановок;

В расчетах используются две подстановки, имеющие частный вид, когда в формуле результативного показателя все факторы взяты на одном аналитическом уровне (базисном или отчетном); их дополнительно определять не нужно, так как это заданный результативный показатель соответственно на базисном или отчетном уровне;

[n+1] - [2] = [n-1] = 4 – число неизвестных подстановок, каждую из которых при анализе используют дважды (один раз в качестве первой подстановки, а второй раз в виде второй подстановки);

[2*(n+1)] = общий объем необходимой информации.

Метод цепных подстановок — прием экономического анализа, используемый для расчета влияния факторов во всех типах детерминированных факторных моделей, кроме обратных аддитивных:

1) аддитивных, которые строятся путем сложения отдельных факторов;

2) мультипликативных, основанных на умножении факторов, под воздействием которых сложился результативный показатель;

3) кратных, в основу построения которых положено деление отдельных факторов, влияющих на анализируемый итоговый показатель;

4) смешанных.

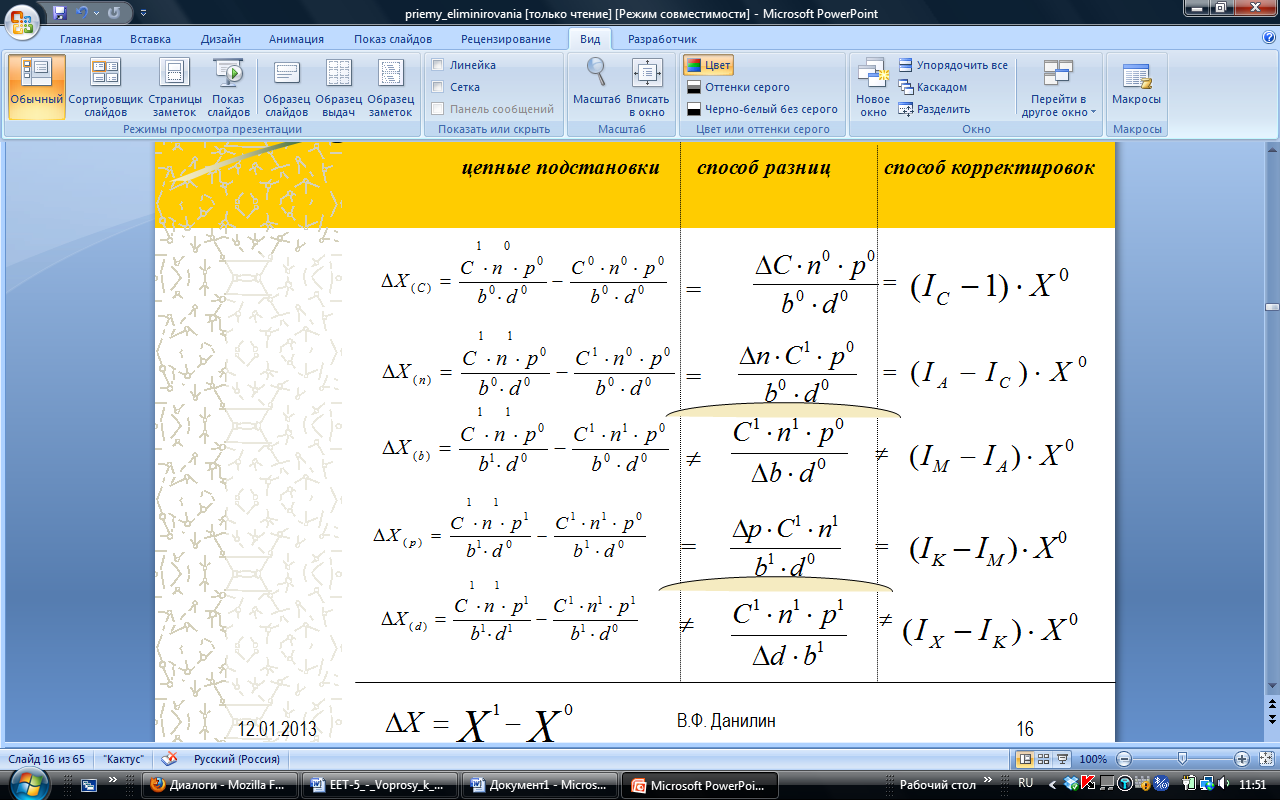
Метод цепных подстановок состоит в последовательной замене базовой величины одного из алгебраических слагаемых или одного из сомножителей фактической величиной, все остальные показатели при этом считаются неизменными. Каждая подстановка связана с отдельным расчетом: чем больше показателей в исходной формуле, тем больше вычислений.

Степень влияния того или иного фактора находится последовательным вычитанием: из результата второй подстановки вычитается первый, из третьей — второй и т.д. В первой подстановке все величины базисные, в последней — фактические. Поэтому число подстановок (расчетов) всегда на единицу больше, чем число показателей исходной формулы. Однако если учесть, что в первой подстановке все величины базисные, а в последней — фактические (отчетные), то общее количество подстановок (расчетов) будет, в конечном итоге, на единицу больше числа показателей исходной формулы.

Алгоритм цепных подстановок как прием последовательного элиминирования целесообразно характеризовать по следующим позициям:

1. Цельпри­ме­н­ения - на­хо­ж­де­ние аб­со­лют­ной ве­личины из­ме­не­ния ре­зуль­та­тив­но­го по­ка­за­те­ля от влия­ния фак­то­ров.

2. Возможности применения (тип модели) – могут ис­поль­зовать­ся за­ви­си­мо­сти лю­бо­го ти­па, кро­ме об­рат­ной ад­ди­тив­ной, т.е. в знаменателе аналитической формулы результативного показателя не должно быть алгебраической суммы факторных признаков.

3. Информационное обеспечение (объем полнота и характер исходных данных) - не­об­хо­ди­мо иметь ин­фор­ма­цию в пол­ном объ­е­ме, т.е. по два значения (в ба­зис­но­м и ана­ли­зи­руе­мо­м пе­рио­де) для ка­ж­до­го фак­тор­но­го при­зна­ка и ре­зуль­та­тив­но­го по­ка­за­те­ля в соответствующих еди­ни­цах из­ме­ре­ния. Сле­до­ва­тель­но, при на­личии в фак­тор­ной сис­те­ме nпер­вичных фак­то­ров все­го по­тре­бу­ет­ся [2(n+1)] дан­ных.

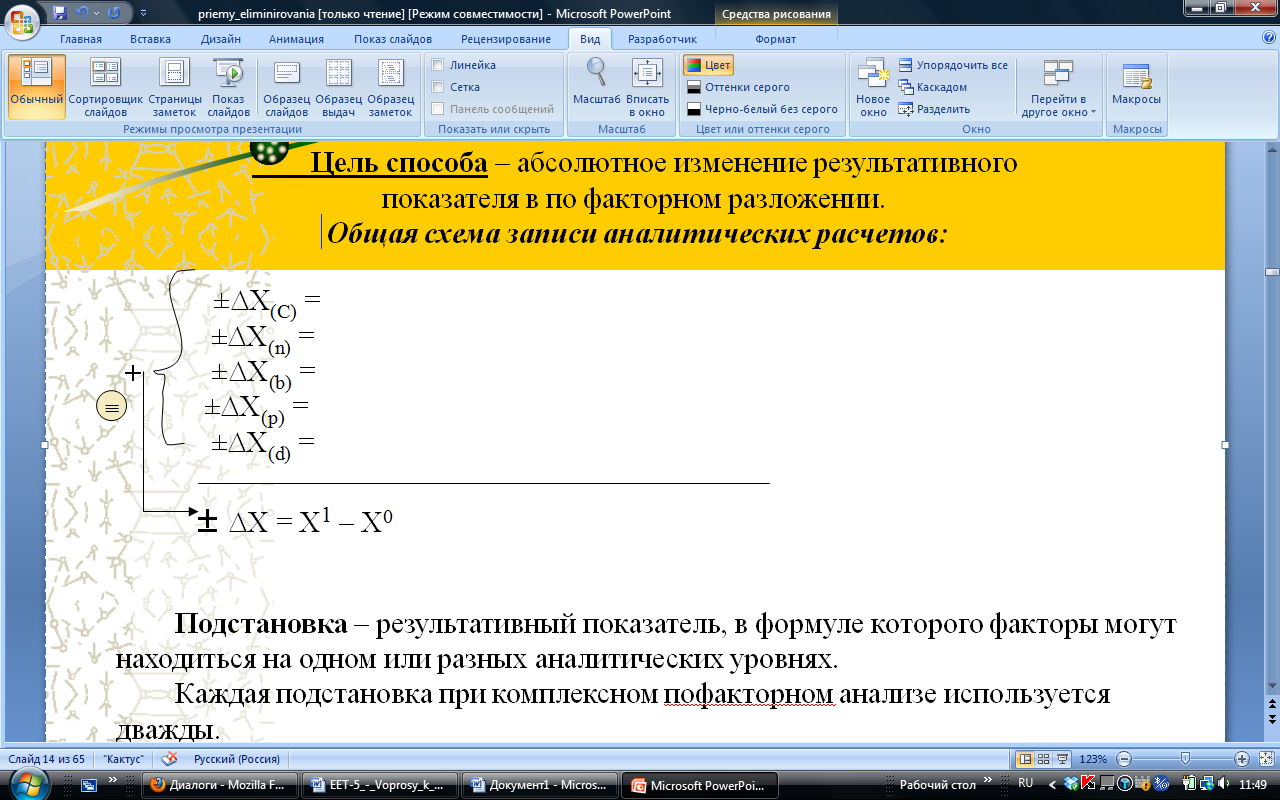
4. Сущность алгоритма. Влия­ние лю­бо­го фак­то­ра на из­ме­не­ние ре­зуль­та­тив­но­го по­ка­за­те­ля оп­ре­де­ля­ет­ся как раз­ность пер­вой и вто­рой под­ста­но­вок. Под­ста­нов­ка - это ре­зуль­та­тив­ный по­ка­за­тель, в ана­ли­тичес­кой фор­му­ле ко­то­ро­го от­дель­ные фак­то­ры мо­гут быть взя­ты на од­ном или раз­ных ана­ли­тичес­ких уров­нях. Пер­вая под­ста­нов­ка от­личает­ся от вто­рой толь­ко од­ним при­зна­ком - уров­нем ана­ли­зи­руе­мо­го фак­то­ра, ко­то­рый в пер­вой под­ста­нов­ке бе­рет­ся фак­тичес­ким, а во вто­рой - ба­зис­ным. Уро­вень ка­ж­до­го из ос­таль­ных фак­то­ров в обе­их под­ста­нов­ках оди­на­ков - фак­тичес­кий, ес­ли они по ус­та­нов­лен­ным ран­гам пред­ше­ст­ву­ют дан­но­му фак­то­ру, и ба­зис­ный для фак­то­ров, сле­дую­щих (по ран­гам) по­сле это­го кон­крет­но­го фак­то­ра. Час­т­ным случаем под­ста­нов­ки яв­ля­ет­ся расчет ре­зуль­та­тив­но­го по­ка­за­те­ля, в ана­ли­тичес­кой фор­му­ле ко­то­ро­го все фак­то­ры бе­рут­ся на од­ном уров­не - ба­зис­ном или фак­тичес­ком.

Вне за­ви­си­мо­сти от слож­но­сти мо­де­ли и числа вхо­дя­щих в ее со­став фак­то­ров количество под­ста­но­вок, не­об­хо­ди­мых для ана­ли­за, оп­ре­де­ля­ет­ся од­но­значно и рав­но: (n+1) все­го под­ста­но­вок и (n-1) не­из­вест­ных ра­нее, где n- чис­ло пер­вичных фак­то­ров, вхо­дя­щих в ана­ли­тичес­кую фор­му­лу расчета ре­зуль­та­тив­но­го по­ка­за­те­ля.

5. Аналитическая проверка полученных результатов. Вы­пол­няется балансовым способом при комплексном анализе по всем первичным факторам. При этом об­щее из­ме­не­ние ре­зуль­та­тив­но­го по­ка­за­те­ля долж­но то­ж­де­ст­вен­но рав­нять­ся ал­геб­раичес­кой сум­ме час­т­ных его из­ме­не­ний от влия­ния всех пер­вичных (вхо­дя­щих в ка­кую - ли­бо фор­му­лу ре­зуль­та­тив­но­го по­ка­за­те­ля) фак­то­ров.

Эф­фе­к­тив­но­е при­ме­не­ние это­го спо­со­ба достигается при последовательном выполнении сле­ду­ю­щих опе­ра­ций:

• проводится ран­жи­ро­ва­ние фак­то­ров;

• берутся две фор­му­лы ре­зуль­та­тив­но­го по­ка­за­те­ля со зна­ком ми­нус ме­ж­ду ни­ми - они не­об­хо­ди­мы для фор­ми­ро­ва­ния пер­вой и вто­рой под­ста­но­вок; ана­ли­зи­руе­мыйфак­тор в пер­вой под­ста­нов­ке берется на фак­тичес­ком уров­не, а во вто­рой - на ба­зис­ном; ос­таль­ныефак­то­ры в обе­их под­ста­нов­ках должны быть на одинаковом уров­не: пред­ше­ст­вую­щие (по ран­гам) за­дан­но­му фак­то­ры - на фак­тичес­ком, а по­сле­дую­щие - на ба­зис­ном;

• выполняются все пре­ду­смот­рен­ные исходной фор­му­лой ариф­ме­тичес­кие опе­ра­ции.

Мо­ди­фи­ка­ци­ей спо­со­ба цеп­ных под­ста­но­вок яв­ля­ют­ся спо­со­б раз­ниц и кор­рек­ти­ро­вок, ал­го­рит­мы ко­то­рых фор­ми­ру­ют­ся пу­тем ал­геб­раичес­ких и ста­ти­стичес­ких пре­об­ра­зо­ва­ний эле­мен­тов ал­го­рит­ма расчета спо­со­бом цеп­ных под­ста­но­вок в це­лях его уп­ро­ще­ния.