19. Метод наименьших квадратов для множественной линейной регрессии.

Метод наименьших квадратов. Общий смысл оценивания по методу наименьших квадратов заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью. Более точно, оценки наименьших квадратов (НК) параметра q получаются минимизацией функции Q по  , где:

Q =  [Y_i - f_i( )]²

Отметим, что f_i( )  - это известная функция  , Y_i = f_i( ) +  _i, где i = от 1 до n,  _i - это случайные величины (например, погрешности измерений), средние которых обычно полагаются равными 0.

20. Геометрическая интерпретация метода наименьших квадратов.

21. Статистические свойства оценок параметров, теорема Гаусса - Маркова.

Если предпосылки метода наименьших квадратов, то оценки, полученные по МНК, обладают следующими свойствами:

1. Оценки параметров являются несмещенными, т. е. M(b₁) = β₁, M(b₀) = β₀ (математические ожидания оценок параметров равны их теоретическим значениям). Это вытекает из того, что M(ε_i) = 0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2. Оценки параметров состоятельны, так как дисперсия оценок параметров при возрастании числа n наблюдений стремится к нулю D(b₀) → 0, D(b₁) → 0 при n → ∞ . По другому говоря, при увеличении объема выборки надежность оценок увеличивается (b₁ наверняка близко к β₁, b₀ — близко к β₀).

3. Оценки параметров эффективны, т. е. они имеют наименьшую дисперсию по сравнению с другими оценками данных параметров, линейными относительно величин y_i.

22. Парные, частные коэффициенты корреляции, совокупные коэффициенты множественной корреляции и детерминации. Понятие и связь между ними.

Парные коэффициенты корреляции. Для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретации аналогичны линейному коэффициенту корреляции в случае однофакторной связи.

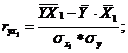
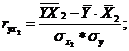
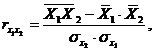
Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели.

Для случая зависимости Y от двух факторов можно вычислить 2 коэффициента частной корреляции:

   

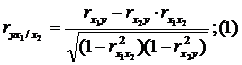
(2-ой фактор   фиксирован);

 

    

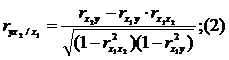
Совокупный коэффициент множественной корреляции или индекс множественной корреляцииопределяет тесноту совместного влияния факторов на результат:

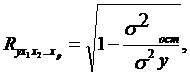
Связь: Частный коэффициент корреляции в отличие от коэффициента (полного) парной корреляции между явлениями показывает тесноту связи после устранения изменений, обусловленных влиянием третьего явления на оба коррелируемых признака (из значений корреляционных признаков вычитаются линейные оценки в связи с третьим признаком).

24. Использование коэффициента детерминации r2 и f-критерия для проверки статистических гипотез о параметрах регрессии.