34. Автокорреляция. Тесты на автокорреляцию остатков (критерий Дарбина-Уотсона).

Автокорреляция — это взаимосвязь последовательных элементов временного или пространственного ряда данных. В эконометрических исследованиях часто возникают и такие ситуации, когда дисперсия остатков постоянная, но наблюдается их ковариация. Это явление называют автокорреляцией остатков.  Существуют два наиболее распространенных метода опреде­ления автокорреляции остатков:

1) построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции.

2)  использо­вание критерия Дарбина — Уотсона и расчет величины:

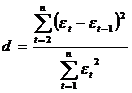
Есть несколько существенных ограничений на применение критерия Дарбина — Уотсона:

1.               Он неприменим к моделям, включающим в качестве независимых переменных лаговые значения результативного признака, т.е. к моделям авторегрессии.

2.               Методика  расчета и использования критерия  Дарбина-Уотсона направлена только на выявление автокорреляции остатков первого порядка.

3.               Критерий Дарбина-Уотсона дает достоверные результаты только для больших выборок.

35. Оценивание при наличии автокорреляции остатков.

Рассмотрим основной подход к оценке параметров модели регрессии в случае, когда имеет место  автокорреляция остатков.

Пусть дана некоторая модель с автокорреляцией остатков:   (1)

И для момента (t-1) это модель принимает вид:   (2)

Умножим обе части уравнения (1) на   :    (3)

Вычтем почленно из уравнения  (1) уравнение (3):

 (4)

Проведя тождественные преобразования в уравнении (4), имеем:

 

36. Прогнозирование в регрессионных моделях. Хуета какая то

37. Система линейных одновременных уравнений и ее идентификация.

Система одновременных уравнений обычно содержит эндогенные и экзогенные переменные.  ^ Эндогенные переменные – взаимозависимы переменные, которые определяются внутри модели (системы)  . Экзогенные переменные – независимые переменные, которые определяются вне системы  .

Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Поэтому рассматриваетсяприведенная форма модели - система линейных функций эндогенных переменных от экзогенных: 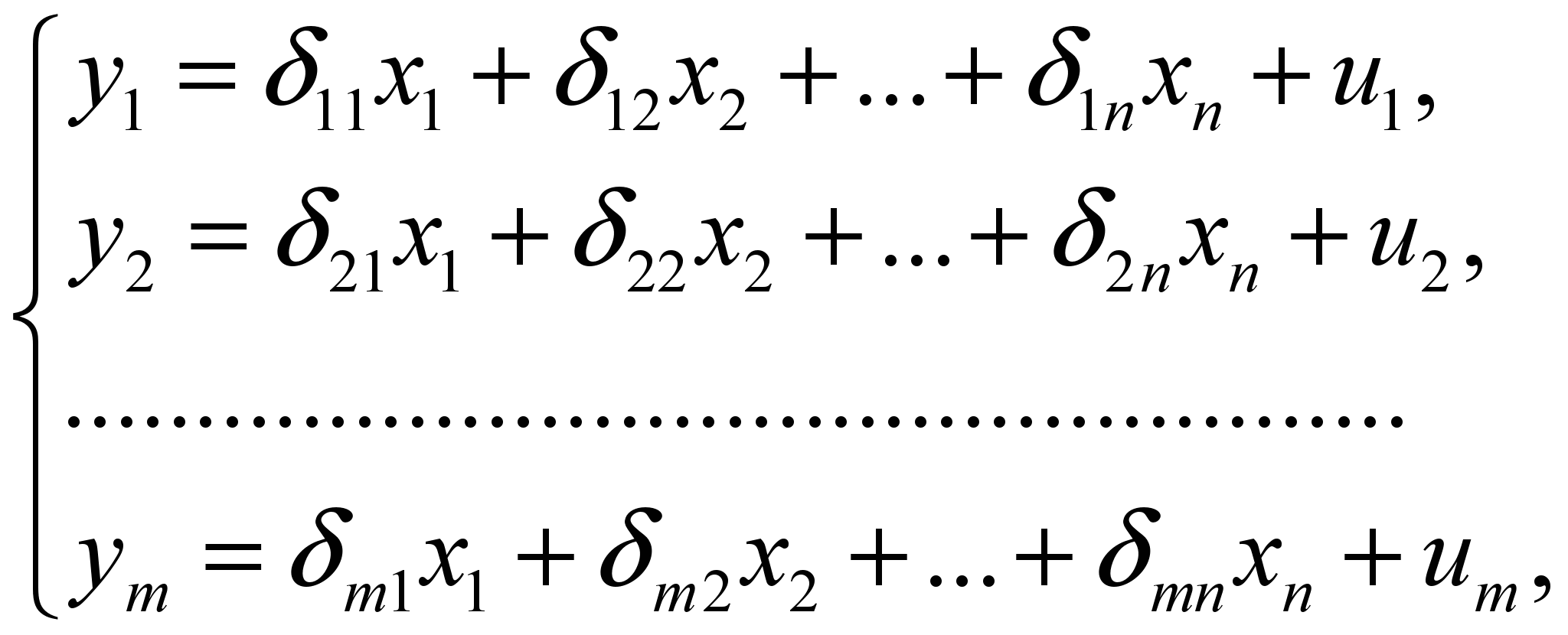 (2) где   – коэффициенты приведенной формы модели,   – остаточная величина для приведенной формы.

При переходе от приведенной формы модели к структурной появляется проблема идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели. Структурная модель (1) в полном виде содержит   параметров, а приведенная форма модели в полном виде содержит   параметров. 

С позиции идентифицируемости структурные модели можно подразделить на три вида:

1. идентифицируемые;

2. неидентифицируемые;

3. сверхидентифицируемые.

38. Приведенная форма структурной модели.

Приведенная форма получается после решения модели относительно эндогенных (внутренних) переменных, то есть выражения этих переменных только через экзогенные (задаваемые извне) переменные и параметры модели. Структурная форма модели содержит эндогенные переменные –  . Это зависимые переменные, число которых равно числу уравнений в системе, и (которые определяются внутри системы).Экзогенные переменные –  . Это независимые переменные, которые определяются вне системы и влияющие на эндогенные переменные, но независящие от них. Лаговые переменные – независимые переменные за предыдущие моменты времени. Лаговыми могут быть эндогенные переменные за предшествующий период времени, и тогда они являются экзогенными.

обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели:

;

;                                         (4)

…

Коэффициенты приведённой формы модели (4) представляют собой нелинейные функции коэффициентов структурной формы модели. Пример простейшей структурной модели:

.

Приведенная форма получается так:

систему одновременных уравнений имеем ,