22.Логарифмическое дифференцирование. Вывод производной степенной ф-ции.

y=a^x - показательная ф-ция, y=xⁿ - степенная, y=x^x - показательно-степенная.

y=[f(x)]^(x) - показательно-степенная ф-ция.

lny=xlnx - найдем производную от левой и правой части, считая у ф-цией х.

(1/y)*y`=(lny)

(x*lnx)`=x`lnx+x*(lnx)`=lnx+1

y`=y*(lnx+1)=x^x(lnx+1)

Операция, которая заключается в последовательном применении к ф-ции y=f(x) сначала логарифмирование, а затем дифференцирование.

Степенная ф-ция:

1.y=xⁿ, nlnx, y`/y=n/x=n*(x)^-1

y`=y*n*(x^-1)=n*xⁿ*x^-1=n*x^n-1

2.y=e^U, где U=sinx

U`=cosx, y`=(e^U)`=e<sup>U</sup>*U`=e^sinx*cosx.

Дифференциал ф-ции и его геометрический смысл. Св-ва дифференциала.

limy=A, y=A+

limy/x=y`, y/x=y`+, y=y`x+x

x0

y=y`x+, где -б.м.в., величина более высокого порядка малости,, чем x(), и ее можно отбросить.

dy=y`x

Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента х и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем х.

Если y=x, то dy=dx=x`x=x, dx=x

Если yx, то dy=y`dx, y`=dy,dx

Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x₀,f(x₀)) при изменении x₀ на величину x

Св-ва: 1. (UV)`=U`V`, то (UV)`dx=U`dxV`dx, d(UV)=d(UV)

2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV

3.d(c)=c`dx=0*dx=0

4. d(U/V)`=(V`dU-U`dV)/V².

21.Уравнение касательной и нормали к кривой.Правила диффиринцирования

Основные правила дифференцирования.

Теорема: Если f(x) и g(x) дифферен. в точке х, то:

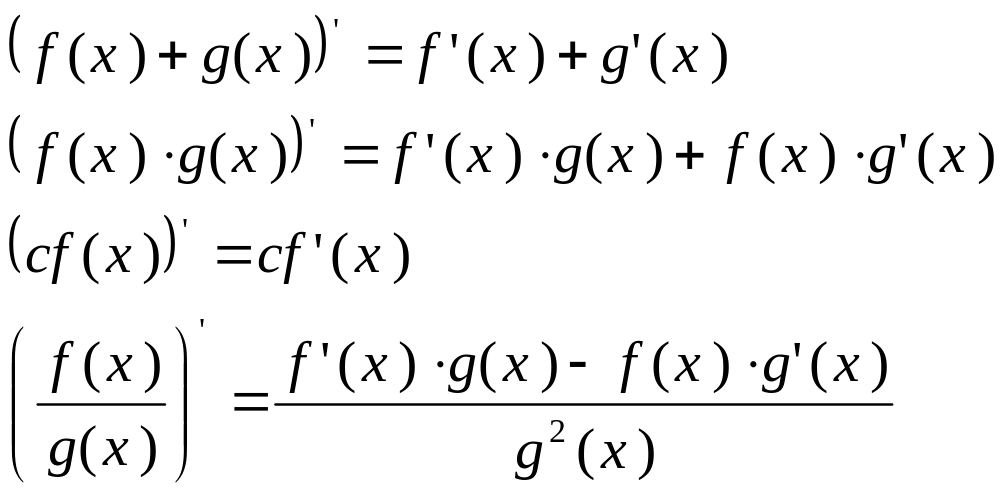
Теорема о произв. сложной функции:

Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).

Теорема о произв. обратной функции.

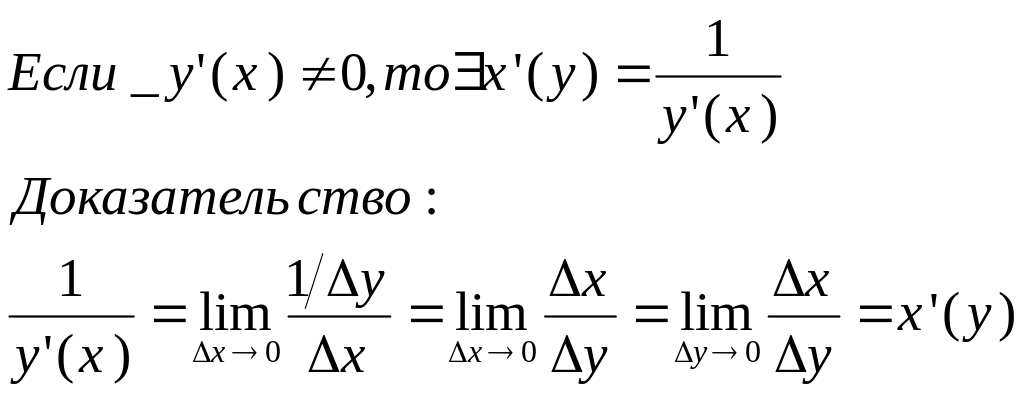
Касательная

Если в качестве M взять кривую, а в качестве m прямую, проходящую через точку O кривой, то при   условие соприкосновения определяет касательную к кривой в точке O (рис. 1). Касательная в точке P кривой также может быть определена как предельное положение секущей, проходящей через P и близкую к ней точку P₁, когда P₁ стремится к P.

Гладкая регулярная кривая в каждой точке имеет определённую касательную. Направление касательной в точке t₀ кривой, задаваемой уравнениями (1), совпадает с направлением вектора  . В векторной записи это производная  .

В дифференциальной геометрии выводятся уравнения касательной для различных способов аналитического задания кривой. В частности, для кривой, задаваемой уравнениями (1), уравнения касательной в точке, отвечающей значению параметра t₀, будут

,

где индекс   указывает на значение функций   и их производных в точке  .

Для плоской кривой уравнение касательной в точке   имеет следующий вид.

• Параметрическое задание: 

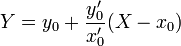
• Явное задание: 

• Неявное задание: 

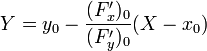
23.Диффиринциал функции . Дифференциал функции в точке

Опр. Диф-м функции в х₀ наз. линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению.

d f(х₀)= f ′ (х₀) ∆х; ∆х=dх; df(х₀)= f ′ (х₀) dх

Геометрический смысл. Уравнение касательной в х₀ эквивалентно уравнению

у=f(х₀)+ f ′ (х₀) ∆х (***)

сравнивая (**) и (***) видим, что расстояние от точки Р(х, f(x)) на графике до точки Q (x, f(х₀)+ f ′ (х₀) ∆х) на касательной равно α(∆х)∆х, т.е. является бесконечно малой более высокого порядка, чем ∆х, когда ∆х→0.

Вывод: геометрический смысл дифференцируемости f(x) в точке х₀ состоит в том, что расстояние от точки на ее графике до соответствующей на касательной стремится к нулю "быстрее", чем ∆х.