Невырожденные кривые

Кривая второго порядка называется невырожденной, если 

Кривая второго порядка называется вырожденной, если Δ = 0

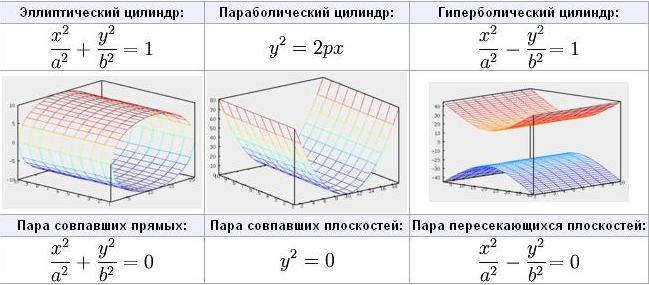
14.Поверхность второго порядка

Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

a₁₁x² + a₂₂y² + a₃₃z² + 2a₁₂xy + 2a₂₃yz + 2a₁₃xz + 2a₁₄x + 2a₂₄y + 2a₃₄z + a₄₄ = 0

в котором по крайней мере один из коэффициентов a₁₁, a₂₂, a₃₃, a₁₂, a₂₃, a₁₃ отличен от нуля.

15.Метод математической индукции

Математическая индукция — в математике — один из методовдоказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.

Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.

Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид

,

где   — биномиальные коэффициенты, n — неотрицательное целое число.

В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное рациональное число (возможно, отрицательное). В этом случае бином представляет собой бесконечный ряд

16.Множество действительных чисел.Понятие функции.

Функции. Определение способа задания. Классификация функций. Основные элементарные функции.

Функция - это зависимость одной величины от другой.

Если существует взаимооднозначное соответствие между переменной х одного множества и переменной у другого множества, то она называется функциональной зависимостью. y=f(x).

Определение способа задания:

-аналитически (y=kx+b)

-графический (график)

-таблично

x	1	2	3
y	4	5	8

-алгоритмически (с помощью ЭВМ)

Классификация функций:

Элементарные: - функции, которые получаются из основных элементарных ф-ций с помощью алгебраических действий (+,-,*,/,введение в степень). Основные элементарные ф-ции:

1. y=xⁿ - степенная

2. y=a^x - показательная

3. y=log_ax - логарифмическая

4. y=sinx, y=cosx - тригонометрические.

Сложные:

Y=f(U), где U=(x), Y=f[(x)]

Если ф-ция у зависит от промежуточного аргумента U, который зависит от независимой переменной х, то y=f[(x)] называется сложным заданием х.