34.Многочлены и их делимость.Теорема Безу.Основная теорема алгебры. Разложение многочлена на множители.Условие тождественности двух многочленов.Признак кратности корня многочлена и функции
Делимость многочлена
Многочлен, который можно представить в виде произведения многочленов низших степеней с коэффициентами из данного поля, называется приводимым (над данным полем), в противном случае — неприводимым. Неприводимые многочлены играют в кольце многочленов роль, сходную с ролью простых чисел в кольце целых чисел. Например, верна теорема: если произведение pq делится на неприводимый многочлен λ, то p или q делится на λ. Каждый многочлен, степени большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулевой степени).
Например, многочлен x4 − 2, неприводимый в поле рациональных чисел, разлагается на три множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.
Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).
Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен отn переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми
Теорема Безу утверждает что остаток от деления многочлена P(x) на двучлен x − a равен P(a).
Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в полевещественных или комплексных чисел).
Основна́я теоре́ма а́лгебры утверждает, что
Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень вполе комплексных чисел.
Разложение многочлена на множители
1.Вынесение множителя за скобку. Из распределительного закона непосредственно следует, что ac + bc = c ( a + b ). Этим можно воспользоваться для вынесения множителя за скобки.
2. Использование формул сокращённого умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.
3. Способ группировки
35.Рациональные функции.Разложение на сумму простейших дробей.Методы нахождения коэфф. Разложения
Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид
где
,
— многочлены от
любого числа переменных.
Частным случаем являются рациональные функции одного переменного:
,
где P(x) и Q(x) — многочлены.
свойства
Любое выражение, которое можно получить из переменных
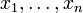с
помощью четырёх арифметических действий,
является рациональной функцией.Множество рациональных функций замкнуто относительно арифметических действий и операции композиции.
Любая рациональная функция может быть представлена в виде суммы простейших дробей (см. Метод неопределённых коэффициентов), это применяется при аналитическом интегрировании.
Простейшими рациональными дробями являются рациональные дроби:
1) 
2) 
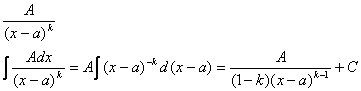
3) 
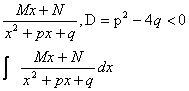
Выделяем полный квадрат и делаем замену переменной:
Тогда интеграл примет вид:
Делаем обратную замену переменной и получаем окончательный ответ.
Разложение правильной рациональной дроби на сумму простейших дробей.