Задача № 1.
,
Дано: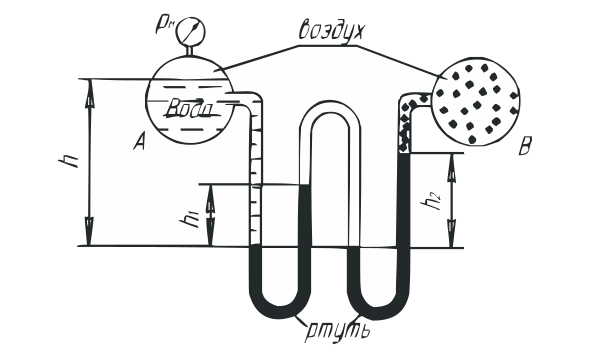
Решение:
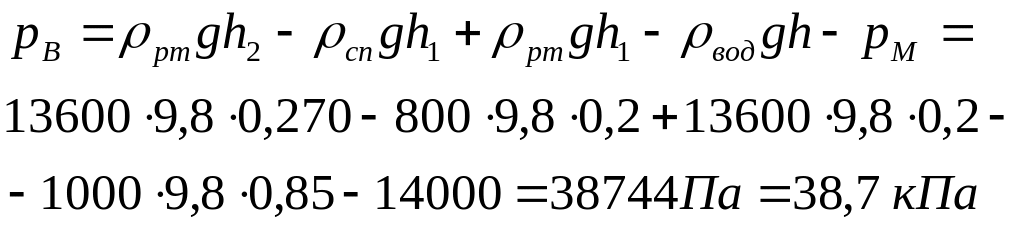
Задача №2
Дано:
Решение: Для
обеспечения равновесия колокола сила
суммарного давления газа Р
на верхнее перекрытие колокола должна
быть равна весу колокола G,
т.е. P
= G.
В то же время сила суммарного давления
на воду под колоколом:
,
где
-
давление газа под колоколом,S
– площадь
колокола.
следует, что:
.
Отсюда площадь колокола:
.
Тогда следует,
что:
.
Давление , действующее на поверхность воды под колоколом, должно быть уравновешено разностью уровней воды Н.
Поэтому:
,
где
Отсюда следует:
Задача №3
l2
l1
l1
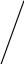
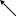
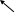
Дано:
Сила суммарного давления воды:
Слева:
=
Справа:
Находим расстояния от шарнира до центров приложения сил давления:
.
.
Составляем уравнение моментов сил относительно шарнира 0:
,
где
.
Следовательно,
усилие:
.
Задача №4
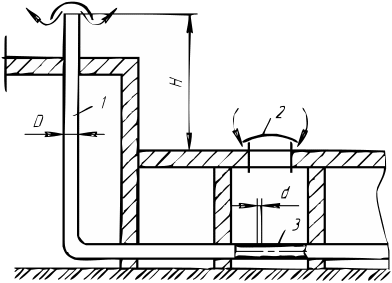
Дано:
Для начала определяем плотности:
Вследствие того,
что в условии не сказано, какой газ
участвует в процессе, то принимаем за
этот газ – воздух, только более высокой
температуры. Другими словами, меняем
местами
и
(потому что у воздуха температура должна
быть более низкой, т.к. в этом случае
плотность будет выше, чем у газа и
соответственно удельный вес
у воздуха будет выше, чем у газа за счёт
чего и происходит вентиляционное
вытеснение газа. .
При
.При
.
Разность напоров связана с разностью давлений формулой:
.
Разность давлений
можно представить так же, как:
.
Откуда следует, что искомая высота:
.
2. Массовый расход в трубе:
.
Необходимо, чтобы
выполнялось следующее условие
(равенство):
,
где
- массовый расход
воздуха через одно приёмное отверстие
диаметра d.
.
Произвольно задаём
количество отверстий:
.
Тогда следует,
что
Задача №5
Дано:
Решение:
Уравнение моментов
сил относительно шарнирной точки 0:
Усилие малого
поршня:
.
Из условия
определим
сжимающее усилие большого поршня:
