Рішення №26

1. Матриця провідностей підсилювача (рис.26) має вид:

1 2

Y=	1	Gе+ +h22e+	-h22e
	2		+h22e+ jω

2. Коефіцієнт передачі напруги =

3. Модуль і аргумент функції відповідно дорівнюють:

Рішення №27

1. Матриця провідностей підсилювача (рис.27) має вид:

1 2

Y=	1	Gб+
	2		+ +h22e+ +jω +

2. Коефіцієнт передачі напруги: =

Модуль і аргумент функції відповідно дорівнюють:

Рішення №28

1. Матриця провідностей моделі підсилювача (рис.28) має вид:

1 2

Y=	1	Gб+
	2		+h22e+ +jωС+

2. Коефіцієнт передачі напруги: =

Модуль і аргумент функції відповідно дорівнюють:

Рішення №29

1. Матриця провідностей моделі підсилювача (рис.29) має вид:

		1	2	3
	1
Y=	3
	4

2. Коефіцієнт передачі напруги :

3. Зображення перехідної H(p) і імпульсної Y(p) характеристик підсилювача відповідно мають вигляд:

H(p)= =

Рішення №30

1. Матриця провідностей моделі підсилювача (рис.30) має вигляд:

   Gв+Gi+S	0	-Gi
   0	Gн+jwc	-jwc
   -Gi-S	-jwc	Gc+Gi+jwc

2. Коефіцієнт передачі напруги:

.

3. Модуль і аргумент крефіцієнта передачі відповідно дорівнюють:

;

,де

.

Рішення №1

1. Згідно системи рівнянь (1) складаємо орієнтований граф(рис.1а):

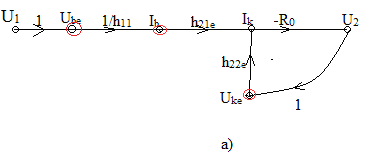
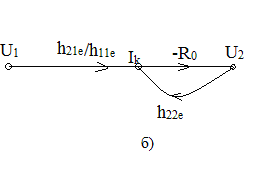
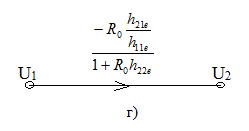
Рис.1

2. Послідовно відстороніємо вершини U_be ,I_b ,U_ke (рис.1б),I_k (рис.1в),петлю графа (рис.1в). Отримаємо граф з двох вершин U₁ і U₂ й передачою Ku (рис.1г).

3. Запишемо формулу Мезона для графа (рис.1а):

де -передача єдиного наскрізного шляху;

-передача єдиного контура;

-доповнення наскрізного шляху.

Рішення №2

1. Запишемо таблицю Рауса:

2	22	60
12	12	0
		0
	0	0
	0	0
0	0	0

З того що коефіцієнти у першому стовпчику таблиці Рауса двічі змінюють знак(з позитивного на негативний,а потім навпаки),можна зробити висновок що дана замкнута система нестійка.

2. Враховуючи перепишемо характеристичне рівняння(годограф Михайлова):

Визначимо частоти, відповідаючі перетину годографа Михайлова-F(jw) з дійсною віссю F_R(w) з рівняння:

Звідки w=w₁=0,

Визначимо частоти ,що відповідають перетину годографа Михайлова F(jw) з уявною віссю F_I(w) з рівняння:

Звідки

Враховуючи ,що , бимо висновок,що замкнута система стійка.