2. Коефіцієнт передачі напруги :

3. Модуль і аргумент коефіцієнта передачі напруги фільтра відповідно дорівнюють:

Рішення №17

1. Матриця провідності моделі LC-генератора (рис.17) має вигляд:

		1,3	2
Y=	1	G3+Gg+jωC+	-G3
	3	G1+G2	-G2

2. Визначник матриці провідності прирівнюємо до нуля:

∆(jω) = ∆_R(ω) + j∆_I(ω) = (G₃+G_g )( -G₂ )+ G₃(G₁+G₂) - jG₂( ωC - )= 0

3. Прирівняти уявну частину ∆_I(ω) = - G₂( ωC - ) = 0 , знаходимо частоту гармонічних коливань ω=ω_r=

4. Прирівнявши дійсну частину ∆_R(ω) = -G_g G₂+ G₃G₁= 0 , знайдемо G_g=

Рішення №18

1. Матриця провідностей моделі LC-генератора (рис.18)

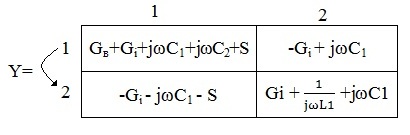2. Визначник матриці Y прирівнюємо до нуля

=[G_в+G_i+jω(C₁+C₂₎+S][ Gi +j(ωC₁+ )] – [G_i + jωC₁][ G_i + jωC₁ + S] = 0

3. Виділяємо дійсну та уявну частини визначника

4. Прирівнюючи дійсну частину до нуля, знаходимо частоту

гармонічних коливань ω_г:

Рішення №19

1. Рівняння вузлової моделі підсилювача (рис.19) має вигляд:

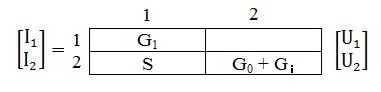
2. Визначаємо вторинні параметри підсилювача:

• коефіцієнт підсилення напруги

• вхідний опір

• вихідний опір

Рішення №20

1. Рівняння вузлової моделі підсилювача (рис.20) має вигляд:

2. Визначаємо вторинні параметри підсилювача:

• коефіцієнт підсилення напруги

• вхідний опір

• вихідний опір

Рішення №21

1. Рівняння вузлової моделі підсилювача (рис.21) має вигляд:

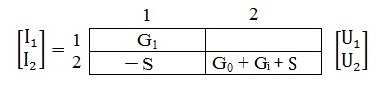
2. Визначаємо вторинні параметри підсилювача:

• коефіцієнт підсилення напруги

• вхідний опір

• вихідний опір

Рішення №22

1. Матриця провідностей підсилювача (рис.22) має вигляд:

2. Коефіцієнт передачі напруги

3. Модуль і аргумент функції відповідно дорівнюють:

Рішення №23

1. Матриця провідностей підсилювача (рис.23) має вигляд:

2. Коефіцієнт передачі напруги

3. Модуль і аргумент функції відповідно дорівнюють:

Рішення №24

1. Матриця провідності (рис.24) має вид:

   		1	2
   Y=	1	G1+jω + jω	-jω
   	2	-jω -S	jω + +jω + jω +S

2. Коефіцієнт передачі напруги

3. Модуль і аргумент функції відповідно дорівнюють:

Ішення №25

1. Матриця провідностей підсилювача (рис.25) має вид:

1 2

Y=	1	Gб+
	2		+h22e+ jω

2. Коефіцієнт передачі напруги =

Модуль і аргумент функції відповідно дорівнюють: