Рішення 1

1.Згідно з теоремою про еквівалентний генератор потенціал бази дорівнює: Потенціал емітера: Потенціал коллектора: Потенціал емітера: = де β= =

2.Рівняння для вихідного і вхідного ланцюгів транзистора у схемі (Рис.1):

Рішення 2

1.Згідно закону Ома потенціали витока і стоку відповідно дорівнюють:

2.Рівняння для вихідного та вхідного ланцюгів транзистора у схемі (Рис.2) дорівнюють: )

Рішення №3

1.Рівняння вузлової моделі підсилювача зі спільним емітером має вид: 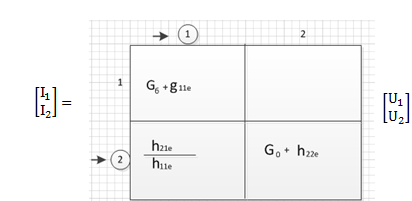2.Коефіцієнт передачи напруги схеми(рис.3): 3.Вихідний опір схеми (Рис.3):

Рішення №4

1.Матриця провідностей моделі підсилювача (рис.4)має вид:

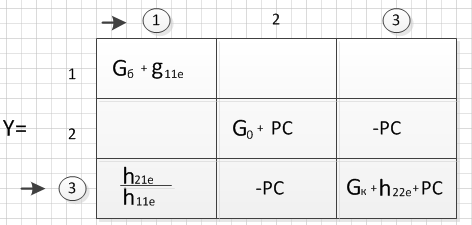
2.Коефіціент передачі напруги схеми(Рис.4): =

3.З врахуванням p=jω знайдемо:

Модуль і аргумент функції ) відповідно дорівнюють: | )|=

Рішення №5

1.Рівняння вузлової моделі мосту Віна(Рис.5) має вигляд:

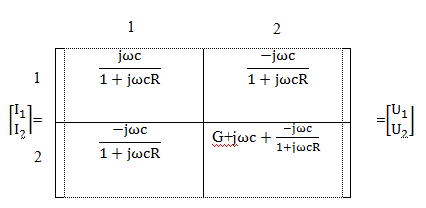
2.Коефіцієнт передачі напруги схеми(Рис.5): = = 3.Визначаємо коефіцієнт передачі напруги на частоті Модуль коефіцієнта передачі напруги Аргумент коефіцієнта передачі напруги: =arctg =0

Рішення №6

1. Матриця провідностей RC-генератора гармонічних коливань з мостом Віна (рис.6) має вигляд:

   	1.3	2	4
   Y = 1
   3
   4

2. Знаходимо визначник матриці провідностей:

3. Прирівнявши дійсну частину визначника до нуля , знаходимо частоту гармонічних коливань .

4. Прирівнявши уявну частину визначника до нуля , отримаємо

Рішення №7

1. Матриця провідностей підсилювача (рис.7) має вид:

   	1	2
   Y = 1
   3	-

2. Коефіцієнт передачі напруги:

3. Вхідний опір:

4. Вихідний опір:

Рішення №8

1. Матриця провідностей неінвертуючого підсилювача (рис. 8):

	1,3	2
Y = 1
3

2. Вторичні параметри підсилювача (рис. 8):

• Коефіцієнт передачі напруги:

• Вхідний опір:

• Вихідний опір:

Рішення №9

1. Матриця провідностей активного фільтра нижніх частот:

	1	2	3,4
Y = 1
3	-
4		-

2. Коефіцієнт передачі напруги:

3. Модуль 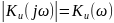і аргумент коефіцієнта передачі напруги відповідно мають вид:

Рішення №10

1. Матриця провідностей активного фільтра нижніх частот:

	1	2	3,4
Y = 1
3	-	-
4		-

2. Коефіцієнт передачі напруги:

3. Модуль і аргумент коефіцієнта передачі напруги відповідно мають вид: