Правило 2.

Район	Элеватор			Запас зерна
	B1	B2	B3
A1	3	5	6	800
	800	-	-
A2	7	2	4	700
	-	700	-
A3	4	3	5	1000
	200	400	400
A4	6	4	7	500
	-	-	500
	1000	1100	900

Просматривается распределительная таблица и в первую очередь заполняется клетка, тариф которой минимальный. В эту клетку записывается максимально возможное значение поставки, затем из рассмотрения исключают строку, соответствующую поставщику, запасы которого исчерпаны, или столбец, соответствующий потребителю, спрос которого удовлетворен. Вновь выбирается клетка с наименьшим тарифом, и процесс завершается, когда запасы исчерпаны и/или запросы потребителей удовлетворены. В процессе заполнения таблицы могут быть исключены строка и столбец одновременно (означает, что задача вырождена и в свободные клетки записывают число 0).

r = 6; f(x) = 2*700 + 3*1200 + 4*200 + 5*400 + 7*500 = 11300.

Элеватор Район		Потребитель			Запас зерна	Этапы
		B1	B2	B3		1	2	3	4
A1		3	5	6	800	2	-	-	-
		100	-	-
A2		7	2	4	700	2	2	-	-
		-	700	-
A3		4	3	5	1000	1	1	1	2
		200	-	800
A4		6	4	7	500	2	2	2	3
		-	400	100
		1000	1100	900
Этапы	1	1	1	1
	2	2	1	1
	3	2	1	2
	4	-	1	2

Правило 3.

В распределительной таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Наибольшая разность отмечается знаком . Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем не рассматриваются. На каждом этапе заполняется только одна клетка. Распределение груза проводится, как и в выше рассмотренных правилах.

f(x) = 3*100 + 4*200 + 2*700 + 4*400 + 5*800 + 7*100 = 8800

Признак оптимальности плана перевозок ТЗ выражается в теореме о потенциалах.

Теорема о потенциалах.

Если план X* = [x_ij]_mxn является оптимальным, то ему соответствует система из m+n чисел u_i* и v_j*, которые удовлетворяют следующим условиям:

Числа u_i и v_j называют потенциалами, соответственно i-го поставщика и j-го потребителя.

Из этой теоремы следуют следующие условия для оптимальности плана перевозок ТЗ:

– каждой занятой клетке распределительной таблицы соответствует сумма потенциалов, равная тарифу этой клетки: u_i+v_j=c_ij.

– каждой свободной клетке соответствует сумма потенциалов, не превышающая тарифа данной клетки: u_i+v_jc_ij.

Метод потенциалов.

Из теоремы о потенциалах вытекает новый метод решения ТЗ – метод потенциалов.

Каждому поставщику ставится в соответствие потенциал u_i, каждому потребителю – v_j. Каждой занятой клетке будет соответствовать уравнение u_i+v_j=c_ij. Всех занятых клеток должно быть на единицу меньше числа потенциалов, поэтому система уравнений неопределенная и одному из потенциалов присваивают произвольное числовое значение (обычно 0). Подставляют это значение в систему и находят остальные потенциалы. Для исследования плана на оптимальность, для каждой свободной клетки проверяется условие u_i+v_jc_ij. Если хотя бы одна клетка не удовлетворяет этому условию, то опорный план не оптимален и его нужно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной является та, для которой разность между тарифом этой клетки и суммой потенциалов минимальна. S_ij(разность) = [c_ij – (u_i + v_j)] < 0. S_ij также является оценкой свободных клеток.

И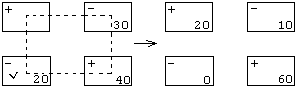 з двух клеток (i,k) и (i,t) с соответствующими оценками S_ik=-5 и S_it=-10 наименьший потенциал имеет (i,t). Величина c_ij показывает, на сколько денежных единиц уменьшатся транспортные издержки от загрузки данной клетки единицей груза. Если для всех свободных клеток оценки S_ij0, то такой план оптимален, причем, если S_ij>0, то план единственный, а если S_ij=0, то планов бесконечное множество, а функция цели при этих планах имеет одно и то же значение.

Если для опорного плана условие оптимальности не выполняется, то план перевозок улучшается за счет загрузки свободной клетки с отрицательной оценкой. Для наиболее перспективной свободной клетки строится замкнутый цикл с вершинами в занятых клетках. Вершинам этого цикла приписывают условно знаки: свободной клетке – «+»; следующей клетке, по или против часовой стрелке, - «-»; далее – «+» и т.д. Из поставок в клетках цикла с отрицательными знаками выбирается наименьшее количество груза, который перемещается по клеткам этого цикла: прибавляется к поставщикам в положительных вершинах и вычитается из поставок в отрицательных вершинах, поэтому баланс цикла не нарушается. Цикл представляет собой замкнутую ломаную линию, состоящую из звеньев, которые пересекаются под прямым углом. Каждое звено соединяет 2 клетки столбца или строки. Цикл включает в себя одну свободную клетку, остальные должны быть заняты. Цикл строится только для свободной клетки.