Двойственность для задач в канонической форме.

Рассмотрим модель симметричной задачи линейного программирования в канонической форме:

; ; x_j  0.

Представим ограничение равенства в виде системы равносильных неравенств.

Умножим второе неравенство на (-1), получим задачу в симметричной форме.

; ; ; x_j  0.

Введем двойственные переменные y_i’, y_i” для каждой системы ограничений.

; ; y_i’  0; y_i”  0.

Введем новые переменные y_i = y_i’– y_i”.

Получим следующий вид двойственной задачи:

; ; y_i.

Рассмотренные выше задачи представляют собой пару не симметричных двойственных задач. Точно так же можно сформировать двойственную задачу со смешанными ограничениями.

Прямая задача

; ; ; x_j  0 (j=1,n); x_j (i=n₁+1,n).

Двойственная задача

; ; ; y_i  0 (i=1,m₁); y_i (i=m₁+1,m).

Двойственная задача со смешанными ограничениями составляется с соблюдением следующих правил:

1. Если на переменные x_j в прямой задаче наложено условие не отрицательности, то j-е условие системы ограничений двойственной задачи записывается в виде неравенства и, наоборот.

2. Если на переменные x_j в прямой задаче не наложено условие не отрицательности, то j-е условие системы ограничений двойственной задачи записывается в виде строгого равенства и, наоборот.

3. Если в прямой задаче имеются ограничения равенства, то на соответствующие переменные двойственной задачи не налагаются условия не отрицательности.

Основные теоремы двойственности и их экономическое содержание.

Основное неравенство теории двойственности:

для любых допустимых планов X = (x₁, x₂, …, x_n) и Y = (y₁, y₂, …, y_n) верно Z(x)  f(y), т.е.

Это значит, что для любого допустимого плана производства Х и для любого допустимого вектора ресурсов Y общая созданная стоимость не превосходит суммарной оценки ресурсов.

Критерий оптимальности Канторовича.

Если для некоторых допустимых планов x* и y* пары двойственных задач выполняется равенство

Z(x*) = f(y*),

то x* и y* являются оптимальными планами соответствующих задач. Это значит, что план производства и вектор оценок являются оптимальными, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.

Принцип двойственности.

Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: Z(x*) = f(y*). Если одна их двойственных задач не разрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений двойственной задачи противоречива. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадает.

Теорема о дополняющей не жестокости.

Для того чтобы планы x* и y* пары двойственных задач были оптимальными необходимо и достаточно выполнение следующих условий:

; .

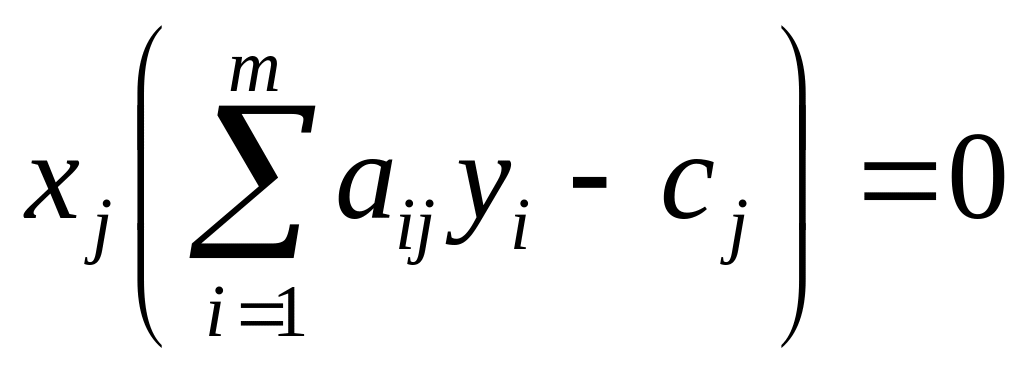Из этих условий следует, что если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи обращается в нуль. Если же какая-либо компонента оптимального плана одной из задач больше нуля, то соответствующее ограничение в двойственной задаче ее оптимального плана должно обращаться в строгое равенство.

Транспортная задача. Постановка транспортной задачи по критерию стоимости в матричной форме. Закрытая и открытая модели транспортной задачи. Построение исходного опорного плана. Метод потенциалов.