Задачи линейного программирования. Задача о наилучшем использовании ресурсов. Задача о выборе оптимальных технологий. Задача о смесях. Задача о раскрое материалов. Транспортная задача. Задача о размещении заказа.

Математическое программирование – область математики, разрабатывающая теорию и численные методы решения задач на экстремум функции нескольких переменных с ограничениями на область значений переменных. Математическое программирование решает экономические задачи.

Целевая функция (критерий оптимальности) – функция, у которой нужно найти экстремум.

Математическая модель задачи включает в себя:

1. План задачи – совокупность неизвестных величин X = (x₁, x₂, …, x_n).

2. Целевая функция – функция, позволяющая выбрать наилучший вариант – Z = z(x), ею может быть прибыль, затраты, товары и др.

3. Система ограничений – условия, которые налагаются на неизвестные величины. Система ограничений в математике выражается в виде уравнений и неравенств, которые называются областью допустимых значений, и обозначаются .

Математическая модель примет вид: Extremum Z = z(x), x  .

В развернутом виде выглядит так: найти план X = (x₁, x₂, …, x_n), доставляющий экстремум функции Z = z (x₁, x₂, …, x_n), при ограничениях _i (x₁, x₂, …, x_n), которые      величин b_i, i=1,m.

Допустимый план – план, удовлетворяющий системе ограниченности.

Оптимальный план – допустимый план, при котором целевая функция принимает экстрем. значения.

Линейное программирование – раздел, применяемый при разработке методов отыскания нескольких переменных при линейных ограничениях. Особенностью задач линейного программирования является то, что целевая функция достигает экстремума на границе области допустимых значений.

Задача о наилучшем использовании ресурсов

Задача: обеспечить предприятию максимальный объем реализации при имеющихся ресурсах.

Для изготовления n видов продукции используют m видов сырья. Запасы сырья – Bi (i=1,m), затраты сырья на изготовление единицы продукции Aij (i=1,m; j=1,n), прибыль от реализации единицы продукции Cj (j=1,n). Необходимо составить план производства Хj (j=1,n), показывающий в каких количествах надо производить продукцию каждого вида, чтобы при ее реализации получить максимальную прибыль. Так как неизвестные величины входят в целевую функцию и систему ограничений в первой степени, то это задача линейного программирования. Общий вид задачи:

, найти , ограничения:

Задача составления рациона (задача о диете, задача о смесях)

Имеется n видов корма, содержащих питательные вещества (витамины) m видов. Содержание витаминов в 1 кг каждого вида корма Aij (i=1,m; j=1,n) и стоимость 1 кг корма Cj (j=1,n).

Требуется составить дневной рацион, в котором содержание каждого вида витаминов было бы не менее установленного минимума Bi (i=1,m), причем затраты на него должны быть минимальными.

, найти , ограничения:

Задача о размещении заказа

Задача: составить план размещения заказа (загрузки оборудования), при котором с имеющимися производственными возможностями план был бы выполнен с наибольшей эффективностью.

На оборудовании m групп выполняется заказ на выпуск n видов продукции в кол-ве Xj* (j=1,n) единиц. Заказ X* определяется в задаче о ресурсах или просто «спущен сверху». Мощность оборудования каждого вида ограничена по времени Ti (i=1,m). Производительность на i-м оборудовании в единицу времени – Aij единиц продукции j-о вида с затратами Cij. Требуется найти план Xij размещения заказа, т.е. установить, сколько времени i-я группа оборудования будет занята изготовлением j-й продукции.

Целевая функция – все затраты на выполнение заказа.

, найти: , ограничения: , ,.

Ограничения по выпуску продукции с опозданием, строго по плану и лишь для загрузки оборудования.

, , .

Задача о раскрое материалов

На раскрой поступает материал в количестве S единиц. Требуется изготовить из него m разных комплектующих изделий в количествах пропорциональных числам Bj (j=1,m) (условие комплектности). Каждая единица материала может быть раскроена n способами. Каждый i-й способ дает Aij единиц j-го изделия. Требуется составить план раскроя, обеспечивающий максимальное количество комплектов.

Xi (i=1,n) – число единиц материала, раскраиваемых i-м способом, и K – число комплектов изделий.

Целевая функция: F=Kmax. Найти . Ограничения:

общее количество материала , , условие комплектности .

Транспортная задача

В m пунктах отправления A₁, A₂, …, A_m сосредоточен однородный груз в количествах a₁, a₂, ..., a_m. Этот груз необходимо доставить потребителям B₁, B₂, …, B_n, спрос каждого потребителя выражается в единицах b₁, b₂, …, b_n. Известна стоимость c_ij перевозки груза из i-го пункта в j-й.

Требуется составить план, который полностью удовлетворяет спрос потребителей, и при этом суммарные транспортные издержки будут минимальными. x_ij – количество единиц груза, который необходимо доставить из i-го пункта отправления в j-й пункт назначения.

Целевая функция: , найти , ограничения:

, .

Задача о выборе оптимальных технологий

Имеется m видов ресурсов Bi (i=1,m). Предприятие может работать по n технологическим способам. Для каждой j-й технологии расход ресурсов за единицу времени равен Aij и производ-ть равна Cj.

Определить интенсивность использования каждого технологического способа Xj (j=1,n).

, найти , ограничения: , .

Геометрическая интерпретация и графическое решение задачи линейного программирования.

Геометрическая интерпретация

Геометрически задача линейного программирования представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции минимальное значение, причем допустимыми решениями служат все точки многогранника решений.

Решение – совокупность чисел х₁, х₂, ..., х_n, удовлетворяющих наложенным ограничениям.

Совместная система неравенств – система, которая имеет хотя бы одно решение. Каждое из неравенств задачи линейного программирования определяет на координатной плоскости X1OX2 некоторую полуплоскость, а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР) или многоугольником решений. Он всегда представляет собой выпуклую фигуру.

Выпуклая фигура – фигура, обладающая следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей.

Многоугольник решений – совокупность точек, координаты которых образуют решения системы. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью. В случае несовместности системы ограничений многоугольник решений является пустым множеством.

Задача

Для более полного представления о задаче линейного программирования сделаем её геометрическую интерпретацию. Рассмотрим задачу:

, ограничения: , .

Порядок графического решения задачи:

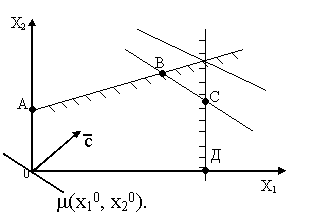1. В ограничениях задачи заменить знаки неравенств знаками точных равенств и построить соответствующие прямые.

2. Найти и заштриховать полуплоскости, разрешенные каждым из ограничений-неравенств задачи.

3. Определить ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделить ее. При отсутствии ОДР задача не имеет решений.

4. Если ОДР не пустое множество, то нужно построить целевую прямую, т.е. любую из линий уровня c₁x₁+c₂x₂=L (где L – произвольное число, например, кратное c₁ и c₂, т.е. удобное для проведения расчетов).

5. Построить вектор – вектор градиентного направления.

6. При поиске максимума целевой функции необходимо передвигать целевую прямую в направлении градиента, при поиске минимума – в обратном направлении. Последняя по ходу движения вершина многоугольника решений будет точкой максимума или минимума целевой функции.

7. Определить координаты точки максимума (минимума) целевой функции x*=(x₁*,x₂*) и вычислить значение Z(x*). Для вычисления координат оптимальной точки x* необходимо решить систему уравнений прямых, на пересечении которых находится x*.

Градиент – вектор, показывающий направление наискорейшего возрастания функции.

, , – градиент.

Линия уровня – прямая, получаемая из целевой функции, при задании ей фиксированного значения: Z=c₁x₁+c₂x₂=const. Изменяя значения целевой функции, получаем семейство прямых, называемых линиями уровня. Линии уровня перпендикулярны вектору градиента.