Классы асинхронных процессов

– Эффективный АП

– из его инициаторов все траектории ведут в результанты;

– каждая из траекторий, приводящих к результанту, начинается в некотором инициаторе;

– АП не содержит ориентированных циклов вне множества результантов.

Эффективность АП позволяет системе быть недетерминированной (т.е. у одного инициатора может быть несколько результантов).

– Управляемый АП:

Если в эффективном АП каждая допустимая последовательность ситуаций классов эквивалентности ведет в один и только один заключительный класс, то ЭАП управляем. В нем все траектории из инициаторов ведут в класс эквивалентности результантов.

– Простой АП

Простой АП – эффективный АП, в котором каждая траектория содержит 1 инициатор и 1 результант.

iI, sS: iFs  sI sS, rR: sFr  sR

Протокол простого ап

АП Р={S,F,I,R} есть АП Р`={S`,F`,I,R}, множество событий которого состоит из объединения инициаторов и результатов S`=IR, а отношение F` I×R (задается на прямом произведении этих множеств). Граф не содержит голых вершин. При переходе от любого АП к его протоколу, все пучки траекторий заменяются на 1 путь. Т.о. в протоколе за каждым инициатором следует результант.

Репозиция АП служит для обновления (возобновления) АП при его повторных активизациях. Репозиция процесса P=(S, F, I, R) – это эффективный АП P’=(S’,F’,I’,R’), такой что

S` IRS<sup>D</sup>, I`R, R`I.

Ситуация S^D – некоторые дополнительные ситуации через которые процесс возобновляется.

Если I’=R и R’=I, то репозиция полная, иначе частичная

Объединение АП и его полной репозиции называют автономным процессом.

Редукция. Суть редукции состоит в сведении данного АП к более простому.

Свойства редукции:

1. Редукция неэффективного процесса может быть эффективным АП.

2. Редукция эффективного АП, если она существует, всегда эффективный процесс.

3. Редукция управляемого процесса, если она существует, всегда управляемый процесс.

4. Редукция частично реализуемого процесса может быть полностью приведенным процессом, а редукция полностью приведенного процесса может быть частично приведенным процессом.

Конечный автомат (КА), его структура и способы задания. Минимизация КА.

Конечный автомат – некоторое устройство, описанное своими событиями и поведением: последовательностью входных воздействий и соответствующих им реакций.

Конечный автомат (детерминированный автомат) – система V={ A, Q, B, ,  }, в которой:

A={ a₁, ..., a_n } – входные символы (входной алфавит);

B={b₁, …, b_m } – выходные символы;

Q={ q₁, ..., q_p } – события (состояния);

: А×Q→Q – функция переходов;

: А×Q→В – функция выходов.

Асинхронный КА – это автомат, в котором при каждом изменении входного символа возникают устойчивые состояния (а, (а,b))= (а,b). Из входа сразу получаем выход.

Свойства КА:

– Отсутствие предвосхищения – выходной сигнал зависит лишь от полученных входов, т.е. автомат не может предвосхитить будущие входы и заранее на них отреагировать. Т.о., имеется некоторая функция выходов, определяющая очередной выход по предшествующему входу.

– Конечная память – автомат имеет конечное множество состояний Q и в каждый момент находится в одном из этих состояний. При получении очередного входа состояние может измениться. Т.о. множество событий задает область памяти автомата.

Детерминированность КА:

– детерминированный автомат – для заданного состояния q_i каждому символу a_j соответствует только одна дуга, выходящая из q_i.

– недетерминированный автомат – функции переходов или выходов задать невозможно:

1. по переходам, когда из одного входа возможны несколько переходов: (а,q_i)=q_j и (а,q_i)=q_m.

2. по выходам, когда из одного входа возможны несколько выходов: (а,q_i)=b_i и  (а,q_i)=b_j.

Инициализация КА:

– инициальный КА – автомат, у которого входной алфавит состоит из одного элемента |А|=1;

– слабо инициальный КА – если 1<|A|<|Q|;

– не инициальный – если |A|=|Q|.

Связность КА:

– сильно связный, если из любого его состояния достижимо любое другое состояние.

– связным, если любое его состояние достижимо из другого состояния без учета направления дуг.

– частичным, если одна из функций не полностью определена.

Способы задания КА:

– Табличный (автоматная таблица)

Н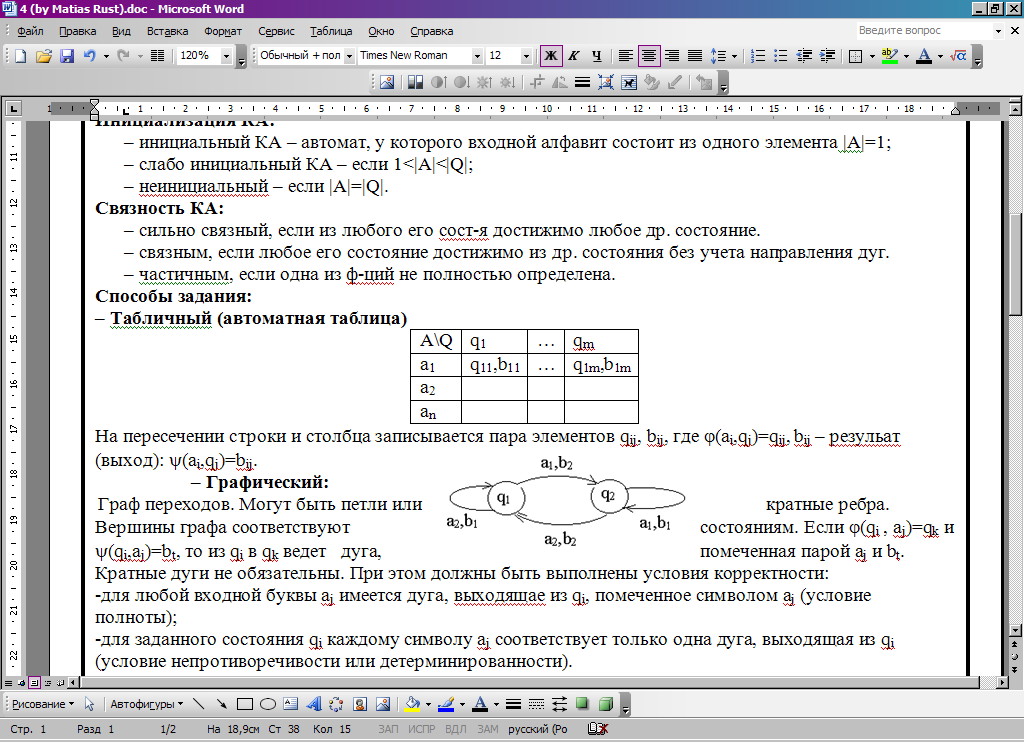 а пересечении строки и столбца записывается пара элементов q_ij, b_ij, где

q_ij – переход, (а_i,q_j)=q_ij;

b_ij – результат (выход), (а_i,q_j)=b_ij.

– Графический

Г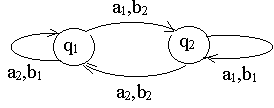 раф переходов. Вершины графа соответствуют состояниям. Если (q_i,a_j)=q_k и (q_i,a_j)=b_t, то из q_i в q_k ведет дуга, помеченная парой a_j и b_t. При этом должны быть выполнены условия корректности:

– условие детерминированности;

– условие полноты – для любой входной буквы a_j имеется дуга, выходящая из q_i, помеченная a_j.

Виды КА:

1. Автомат Мура: функция выходов не зависит от входа.

2. Автомат «Часы»: функция переходов не зависит от входа.

3. «Автономный» автомат: обе функции не зависят от входов.

4. «Переходная система»: граф автомата имеет петли, φ(а,q)=q.

5. Автомат «без памяти»: множество состояний одноэлементно, |Q|=1.

6. Автомат «без потери информации»:

функция выходов задает взаимно однозначное соответствие А на В.

Эквивалентность автоматов

Два конечных автомата эквивалентны, если их поведение одинаково. Т.е. у них одинаковое множество ситуаций, одинаковые входы и выходы, функции переходов и выходов совпадают.

Переход от автомата V к эквив. автомату называется эквив. преобразованием автомата V.

Минимизация конечных автоматов

Задача минимизации числа состояний автомата: среди автоматов, эквивалентных V, найти автомат с наименьшим числом состояний – минимальный автомат.

Алгоритм нахождения эквивалентных состояний Мили.

Он основывается на разбиении множества L на классы эквивалентности. Каждый следующий шаг получается в разбиении предыдущих классов эквивалентности:

1. Исключить все недостижимые состояния.

2. Построить классы эквивалентности.

3. Каждый из этих классов становится состоянием нового автомата.

4. Функция переходов строится на основании функции переходов исходного автомата и новых состояний.

Пример:

Автоматы-распознаватели и автоматы-преобразователи.

КА-распознаватель – распознает слова и отвечает на вопрос, принадлежит ли поданное на вход слово наперёд заданному множеству.

Лук

КА-преобразователь – содержит 2 ленты: входную и выходную. Исходя из задания автомата требуется определить отображение входных слов в выходные. (Построим автомат, который удаляет лишние пробелы за пробелами).

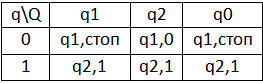
q1 – прочитал пробел, q2 – прочитал символ, q0 – ничего не прочитал.

Семантика языка программирования. Виды семантик.

Язык программирования – формальная знаковая система, предназначенная для описания алгоритмов в форме, которая удобна для исполнителя (например, компьютера). Язык программирования определяет набор лексических, синтаксических и семантических правил, используемых при составлении компьютерной программы. Он позволяет программисту точно определить то, на какие события будет реагировать компьютер, как будут храниться и передаваться данные, а также какие именно действия следует выполнять над этими данными при различных обстоятельствах.

Синтаксис языка – описывает структуру программ как наборов символов безотносительно к содержанию.

Семантика языка – определяет смысловое значение предложений алгоритмического языка.