Сети Петри (СП): структура, выполнение. Анализ СП деревом достижимости.

С ети Петри – математический аппарат для моделирования динамических дискретных систем. Впервые описаны немецким математиком Карлом Петри в 1962 году.

Структура

Сеть Петри представляет собой двудольный* ориентированный граф, состоящий из вершин двух типов – позиций и переходов, соединённых между собой дугами, вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры, фишки), способные перемещаться по сети.

Сеть Петри – это четверка ‹P,T,I,O›, где P – множество позиций, T – множество переходов, I и O – соответственно входные и выходные функции – отображение переходов в комплекты позиций.

Выполнение

Сеть Петри выполняется посредством запусков переходов. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции. Переход может запускаться только в том случае, когда он разрешен. Запуски могут осуществляться до тех пор, пока существует хотя бы один разрешенный переход. Когда не останется ни одного разрешенного перехода, выполнение прекращается.

Разрешенный переход – переход, у которого каждая из его входных позиций имеет число фишек, по крайней мере, равное числу дуг из позиции в переход.

Разрешающие фишки перехода – фишки во входной позиции, которые разрешают этот переход.

Тупик сети Петри – это множество переходов, которые в некоторой маркировке не разрешены.

Ресурс – позиция, являющаяся разрешенной, но не имеющая прямого отношения к процессу.

Маркировка сети Петри – это функция, отображающая множество позиций на множество натуральных чисел. Маркировку можно также определить как вектор.

Маркированная сеть Петри С = <P, T, I, O,μ> есть совокупность структуры сети Петри <P, T, I, O> и маркировки μ.

Свойства сетей Петри

– ограниченность – число меток в любой позиции сети не может превысить некоторого значения K;

– безопасность – частный случай ограниченности, K=1;

– сохраняемость – постоянство загрузки ресурсов,

постоянна, где – число маркеров в i-той позиции, – весовой коэффициент;

– живость – возможность срабатывания любого перехода при функционировании моделируемого объекта.

– устойчивость – для любых двух разрешённых переходов срабатывание одного не приводит к запрещению другого.

– активность перехода – каждый переход может обладать одним из пяти уровней активности:

– 0-й уровень (пассивность перехода) – у перехода отсутствует достижимая маркировка, в которой он разрешен.

– 1-й уровень – переход потенциально достижим, т.е. существует допустимая маркировка, в которой он разрешен.

– 2-й уровень – существует послед-сть запусков переходов, где этот переход присутствует ограниченное число раз.

– 3-й уровень – есть бесконечная послед-ть запуска переходов, где этот переход присутствует неограниченно часто.

– 4-й уровень – переход разрешен в любой допустимой маркировке.

Задачи сетей Петри

– достижимость – является ли маркировка m1 достижимой из начальной маркировки m0?

– покрываемость – является ли маркировка mn покрывающей для маркировки mk при начальной маркировке m0?

– последовательность запусков – возможна ли другая последовательность запусков переходов в данной сети?

– эквивалентность и подмножества – можно ли изменить послед-ть запусков переходов, не изменяя поведение сети?

Достижимая маркировка – маркировка m1 достижима из m0, если существует послед-ть переходов, переводящая m0 в m1.

Покрывающая маркировка – маркировка m1 покрывает m2, если у m1 в каждой позиции фишек не меньше, чем у m2.

Д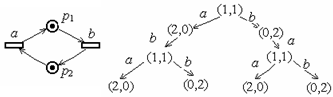 ерево достижимости представляет все достижимые маркировки сети Петри, а также все возможные последовательности запусков ее переходов. При построении конечного дерева достижимости для обозначения ∞ множества значений маркировки позиции используется символ w.

Анализ свойств и задач сети Петри на основе дерева достижимости

– ограниченность и безопасность – Сеть Петри ограниченна, когда символ w отсутствует в ее дереве достижимости. Отсутствие символа w означает, что множество достижимых маркировок конечно. Следовательно, простым перебором можно найти верхнюю границу, как для каждой позиции, так и общую.

– сохраняемость – т.к. дерево достижимости конечно, для каждой маркировки можно вычислить ее сумму. Если эти суммы одинаковы для всех маркировок, то сеть Петри является сохраняющей.

– живость и активность перехода – переход t сети Петри является потенциально живым, тогда и только тогда, когда он хотя бы раз отмечен на некоторой дуге в дереве достижимости сети.

– достижимость – задача решается путём простого перебора вершин дерева достижимости.

Ограниченность метода

К сожалению, в общем случае дерево достижимости нельзя использовать для решения задач достижимости и активности, эквивалентности. Решение этих задач ограничено существованием символа w. Символ w означает потерю информации: конкретные количества фишек отбрасываются, учитывается только существование их большого числа.

*Двудольный граф или биграф – граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.

Анализ СП матричным методом. Задачи, решаемые СП.

Представление сети матричным способом

Матричная форма представления сети C = (P, T, D^–, D⁺). Входная и выходная функции представляются матрицами D⁺ и D^–. (D⁺ – D^–) = D – составная матрица изменений, элементы которой м/б отрицательными, D_j – j-й столбец матрицы D.

Результат запуска перехода t_j в маркировке μ равен

.

Тогда для последовательности запусков переходов имеем

,

где f(σ) – вектор запусков последовательности σ, каждый элемент которого показывает число запусков соответствующего перехода. Все элементы этого вектора неотрицательны.

Анализ свойств сетей Петри матричным методом

– Сохраняемость

Для того чтобы показать сохранение сети, необходимо найти ненулевой вектор взвешивания ω длиной n, для которого взвешенная сумма по всем маркировкам постоянна, т.е. ωμ = ωμ'. Поскольку маркировка μ' достижима, существует последовательность запусков переходов σ, которая переводит сеть из μ в μ':

Получаем

Поскольку это должно быть справедливо для всех , то .

Сеть Петри является сохраняющей тогда и только тогда, когда существует такой вектор ω, что ωD = 0. Если ω = (1, 1, ..., 1), то условие получается таким: сумма элементов каждого столбца матрицы D должна быть нулевой.

– Достижимость

Предположим, что маркировка μ' достижима из маркировки μ. Тогда существует последовательность запусков переходов σ, которая приводит из μ к μ'. Это означает, что f(σ) является неотрицательным целым решением следующего матричного уравнения для х:

Если уравнение не имеет неотрицательного целого решения, то μ' недостижима из μ. Наличие решения уравнения является необходимым, но не достаточным для достижимости. Необходимо проверить, существует ли разрешенная последовательность запуска переходов, соответствующая вектору разметки μ'.