Алгоритм сортировки выбором.
Шаги алгоритма:
находим минимальное значение в текущем списке
производим обмен этого значения со значением на первой неотсортированной позиции
теперь сортируем хвост списка, исключив из рассмотрения уже отсортированные элементы
Пирамидальная сортировка сильно улучшает базовый алгоритм, используя структуру данных «куча» для ускорения нахождения и удаления минимального элемента.
Существует также двунаправленный вариант сортировки методом выбора, в котором на каждом проходе отыскиваются и устанавливаются на свои места и минимальное, и максимальное значения.
http://ru.wikipedia.org/wiki/Сортировка_выбором
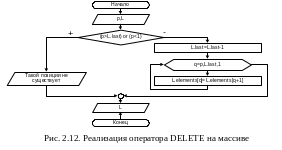
Алгоритм удаления элемента линейного списка.
Алгоритмы поиск элемента в массиве.
(МАКСИМАЛЬНОГО ЭЛЕМЕНТА И МИНИМАЛЬНОГО)
Пусть в переменной с именем Max хранится значение максимального элемента массива, а в переменной с именем Nmax - его номер. Предположим, что первый элемент массива является максимальным, и запишем его в переменную Max, а в Nmaxзанесем его номер, то есть - 1. Затем все элементы, начиная со второго, сравниваем в цикле с максимальным. Если текущий элемент массива оказывается больше максимального, то записываем его в переменную Max, а в переменную Nmax - текущее значение индекса i.
Алгоритм поиска минимального элемента в массиве будет отличаться от приведенного выше лишь тем, что в условном блоке знак поменяется с > на <.
Алгоритмы порождения кодовых слов в порядке двоичного счета.
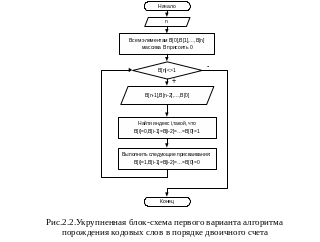
Наиболее прямым способом порождения данной последовательности кодовых слов является счет в системе счисления с основанием 2, что реализует алгоритм, представленный укрупненной блок-схемой на рис.2.2.
Укрупненная блок-схема показывает идеи алгоритма и не расскрывает многие детали реализации. В рассматриваемом алгоритме из укрупненной блок-схемы видно, что двоичные наборы длины n формируются в ячейках B[n-1],B[n-2],...,B[0], массива B. Ячейка B[n] массива B служит для организации завершения работы алгоритма. Ячейка B[n] принимает значение 1, когда все 2n наборов выданы. Также видно, что для реализации двоичного счета, т.е. для организации перехода от текущего кодового слова к следующему, используется простой прием:
просматривается текущее кодовое слово в направлении от младшего разряда к старшему с целью поиска первого разряда, равного нулю (на укрупненной блок-схеме номер такого разряда сохраняется в переменной i);.
найденному первому разряду, равному нулю, присваивается значение 1, а все «более младшие» разряды, значение которых равно 1, обнуляются.
Однако из укрупненной блок схемы не видны детали реализации перехода от текущего кодового слова к следующему. Обычно подобная детализация не вызывает трудностей.
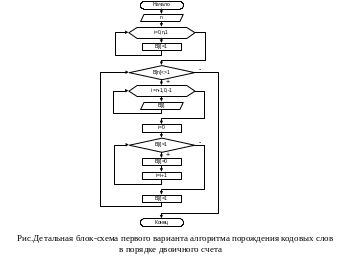
В некоторых случаях будем приводить детальные блок-схемы алгоритмов. Поскольку алгоритм порождения кодовых слов в порядке двоичного счета является первым рассматриваемым нами алгоритмом, то приведем его детальную блок-схему. Детальная блок-схема алгоритма представлена на рис. 2.3.
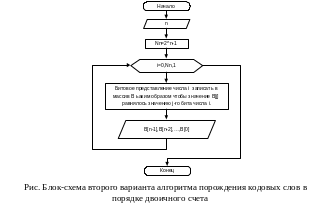
Еще один способ порождения последовательности кодовых слов в порядке двоичного счета заключается в переборе всех целых чисел от 0 до 2n-1 и обращением двоичного представления каждого из чисел в набор (bn-1,bn-2,...,b0). Обращение осуществляется с помощью битовых операций или с помощью операций целочисленного деления и получения остатка от деления.
Укрупненная блок схема алгоритма реализующего данный подход показана на рис.2.4.
