55. Хранение графа с помощью массивов смежности.

Объем памяти можно существенно уменьшить, если упаковывать матрицы в массивы смежности. Пример упаковки рассмотренной матрицы весов (табл. 2.6) в массивы приведен на рис. 2.19.

Упаковка осуществляется с помощью трех массивов: S, V и U. Заполнение массивов S и V осуществляется путем построчного просмотра матрицы. При просмотре текущей строки матрицы в массиве S сохраняются номера столбцов, содержащие значения, отличные от , сами значения сохраняются в массиве V. Массив U служит для разграничения информации в массивах S и V, i-ый элемент массива U содержит индекс массивов S и V, с которого начинается информация, относящаяся к i-ой строке матрицы. Таким образом, для нахождения вершин, смежных i-ой вершине, и весов соответствующих дуг по массивам смежности необходимо вычислить начальный In и конечный Ik индексы в массивах V и S по формулам: In=U_i; Ik=U_i+1-1. Тогда S_In,S_In+1,…,S_Ik - вершины, смежные i-ой вершине, V_In,V_In+1,…,V_Ik – длины дуг (i,S_In),(i,S_In+1,),…,(i,S_Ik). Если Ik=U_i+1-1 окажется меньше In=U_i, то это означает, что i-я строка матрицы весов содержит одни , т.е. i-я вершина не имеет смежных вершин.

Для хранения упакованной таким образом матрицы весов понадобится 43 ячейки памяти, занимаемых массивами V,S и U. Неупакованная матрица занимала 1010=100 ячеек памяти.

Если упаковывается матрица смежности, то массив V не нужен.

Таблица 2.6.
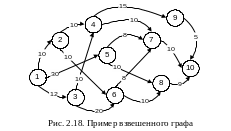
Матрица весов графа, изображенного на рис.2.18
	10	12		30					
			10		10				
			10		20				
						10		15	
						8	10		
						8	10		
									10
									9
									5
									

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
V	10	12	30	10	10	10	20	10	15	8	10	8	10	10	9	5
S	2	3	5	4	6	4	6	7	9	7	8	7	8	10	10	10
U	1	4	6	8	10	12	14	15	16	17	17
Рис.2.19. Упаковка матрицы весов (табл. 2.6) в массивы смежности