Алгоритм бинарного поиска элемента в массиве.
Если у нас есть массив, содержащий упорядоченную последовательность данных, то очень эффективен двоичный поиск.
Переменные Lb и Ub содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Мы начинаем всегда с исследования среднего элемента отрезка. Если искомое значение меньше среднего элемента, мы переходим к поиску в верхней половине отрезка, где все элементы меньше только что проверенного. Другими словами, значением Ub становится (M – 1) и на следующей итерации мы работаем с половиной массива. Таким образом, в результате каждой проверки мы вдвое сужаем область поиска. Так, в нашем примере, после первой итерации область поиска – всего лишь три элемента, после второй остается всего лишь один элемент. Таким образом, если длина массива равна 6, нам достаточно трех итераций, чтобы найти нужное число.
Двоичный поиск - очень мощный метод. Если, например, длина массива равна 1023, после первого сравнения область сужается до 511 элементов, а после второй - до 255. Легко посчитать, что для поиска в массиве из 1023 элементов достаточно 10 сравнений.
Алгоритм быстрой сортировки.
выбрать элемент, называемый опорным (С точки зрения корректности алгоритма выбор опорного элемента безразличен. Известные стратегии: выбирать постоянно один и тот же элемент, например, средний или последний по положению; выбирать элемент со случайно выбранным индексом.);
сравнить все остальные элементы с опорным, на основании сравнения разбить множество на три — «меньшие опорного», «равные» и «большие», расположить их в порядке меньшие-равные-большие.
повторить рекурсивно для «меньших» и «больших».
Быстрая сортировка использует стратегию «разделяй и властвуй».
Алгоритм вычисления контрольного разряда штрих-кодов формата EAN.
Для расчета контрольного разряда в EAN-8, EAN-13, а также в форматах EAN-14 (ITF-14), UPC-A и UPC-E, используется один и тот же алгоритм вычислений («по модулю 10»):
Пронумеровать все разряды справа налево (например, от 1 до 13 для EAN-13), начиная с позиции контрольного разряда.
Шаг 1: Начиная со 2-го, сложить значения всех ЧЕТНЫХ разрядов.
Шаг 2: Полученную сумму умножить на 3.
Шаг 3: Начиная с 3-го, сложить значения всех НЕЧЕТНЫХ разрядов.
Шаг 4: Сложить результаты, полученные во 2 и 3 шагах.
Шаг 5: Значение контрольного разряда является наименьшим числом, которое в сумме с величиной, полученной в шаге 4, дает число, кратное 10.
Рассмотрим пример расчета контрольного разряда С для кода 560172111001С (формат EAN-13).
Шаг 1. Сложить цифры, стоящие на четных местах: 6+1+2+1+0+1=11,
Шаг 2. Полученную сумму умножить на 3: 11*3=33,
Шаг 3. Сложить цифры, стоящие на нечетных местах, без контрольной цифры: 5+0+7+1+1+0=14,
Шаг 4. Сложить числа, полученные при выполнении 2 и 3 шагов: 33+14=47,
Шаг 5. В числе 47 отбросить десятки - получим 7, 10-7=3.
Итак, после расчета контрольного разряда получим код 5601721110013.
Алгоритм линейного поиска элемента в массиве.
Принцип работы заключается в том, что каждый элемент массива сравнивается с ключем поиска на случай совпадения. Метода линейного поиска лучше всего использовать в небольших или в несортированных массивах. В иных случаях он малоэффективен и на выручку приходит метод двоичного поиска.
Алгоритм нахождения суммы элементов массива.
Пусть дан массив A, состоящий из n элементов: a1, a2, a3, …, an. Нужно найти их сумму, т.е. S=a1+a2+a3+…+an.
Нахождение суммы есть последовательное нахождение суммы по формулам:
S=0 S=S+a2 … S=S+ai S=S+an
S=S+a1 S=S+a3 …
Алгоритм вычисления суммы удобно организовать циклом, взяв за параметр цикла переменную i, которая меняется от 1 до n с шагом 1, и записав в цикле формулу S=S+ai один раз. Схема алгоритма приведена на рис. 1а.
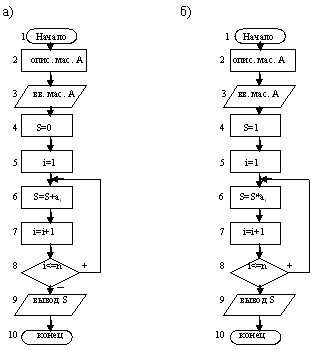
В схеме блок 4 присваивает S нулевое значение, блок 5 счетчику i присваивает начальное значение, блок 6 выполняет накопление суммы, блок 7 изменяет значение i на 1, блок 8 осуществляет проверку условия повторения цикла. При выполнении этого условия управление передается в начало цикла, а при невыполнении – осуществляется выход из цикла, т.к. при i=n+1 суммировать не нужно. n – в схеме предполагается число, но n может быть и переменной, значение которой равно числу элементов массива A, которое нужно вводить перед описанием массива.
При разработке этого алгоритма учащимся можно предложить изменить схему на случай, если нужно найти сумму элементов, расположенных на четных местах в массиве A (Ответ: Блок 5 надо изменить на i=2 и блок 7 на i=i+2) или задать вопрос – что изменится в схеме на рис.1а, если суммировать только положительные элементы массива A? (Ответ: Перед блоком суммирования 6 нужно поставить блок проверки элемента массива ai на положительность и, если он положителен, то его суммировать, а если нет, то обходить блок суммирования.)
что добавить в схеме, чтобы в ней подсчитывалось еще количество положительных элементов массива?
Ответ: Надо ввести переменную k для получения количества положительных элементов и перед циклом присвоить ей значение 0. После блока проверки 7 по пути “+” нужно поставить блок, содержащий k=k+1, который ведет счет количества положительных элементов массива A.
http://festival.1september.ru:8080/articles/101502/
Алгоритм нахождения суммы элементов матрицы.(??????????????)
Рассмотрим задачу нахождение сумм элементов строк матрицы на примере задачи подсчета итогов футбольного чемпионата.
Пусть задана таблица результатов игр 5 команд футбольного чемпионата размера 5х5. На диагонали таблицы стоят значения 0, другие элементы таблицы равны 0, 1 или 2, где 0 баллов соответствует проигрышу команды в игре, 1 балл - ничьей, 2 балла - выигрышу. Определить сумму баллов каждой команды по результатам чемпионата.
Легко заметить, что для построения матрицы R результатов игр достаточно ввести лишь стоящую выше (или ниже) главной диагонали половину матрицы, т.к. результаты остальных игр могут быть рассчитаны из известного соотношения: если, например, первая команда обыграла вторую, то элемент R[1,2]=2, а элемент R[2,1]=2-R[1,2]=0; аналогично, если вторая команда сыграла в ничью с третьей, то R[2,3]=1, R[3,2]=2-R[2,3]=1. Таким образом, нетрудно получить вид взаимосвязи элементов матрицы: R[i,j]+R[j,i]=2, где i и j меняются от 1 до 5 (кроме элементов главной диагонали). На главной диагонали матрицы R по условию задачи всегда стоят числа 0.
Алгоритм пирамидальной сортировки.
Идея использования информации, полученной при вычислении максимума на предыдущем шаге алгоритма выбора, реализована в алгоритме пирамидальной сортировки. Пусть исходный файл, взятый для примера:
503 87 512 61 908 170 897 275 653 426 154 509 612 677 765 703
представлен в виде бинарного дерева, описывающего турнир с выбыванием, аналогичный спортивным соревнованиям. Элемент "побеждает" в соревновании двух элементов файла, если его ключ больше. Меньший ключ, "проигрывая" соревнование, выбывает из дальнейшей борьбы за максимальное значение. Дерево имеет следующий вид.
908
703 897
653 426 612 765
275 503 87 154 509 170 677 512
61
В данном бинарном дереве каждый предок больше обоих своих потомков, и в корне находится наибольший ключ. Такое дерево, названное пирамидой, и определило название метода.
Структуру данных для представления пирамиды удобно выбрать в виде последовательного списка ключей, так что для каждого ключа K[i] его правый и левый сыновья находятся в позициях 2*i и 2*i+1 (ключи K[2*i] и K[2*i+1]). Например, вышеприведенная пирамида из 16 ключей отображается таким последовательным списком:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
908 703 897 653 426 612 765 275 509 87 154 509 170 677 512 61
└──┼╨──┼╜ │║ │║ └╫──┼╫──┼╫───╫──╫───╫───╨───╜ ║ ║ ║
└───┼────┼╨──┼╜ ║ └╫──┼╫───╫──╫───╫───────────╨───╜ ║
└────┼───┼────╨───╜ └╫───╫──╫───╫──────────────────╜
└───┼────────────╨───╜ ║ ║
└───────────────────╨───╜
После удаления максимального элемента из корня и переноса его в выходной массив необходимо скорректировать пирамиду так, чтобы в корне был следующий максимальный элемент, а каждый предок был больше своих потомков. Процесс продолжается до тех пор, пока в сортирующем дереве не останется один элемент.
http://techn.sstu.ru/TFI/site_tfi/TFI/PVS/material/murashev/programming/term2/books/sort.htm#_Toc38711146