6. Решение слау методом Крамера.

Пример. Найдите решение системы линейных уравнений методом Крамера . Решение. Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле Имеем Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители : Таким образом, Ответ: . Обозначения неизвестных переменных в уравнениях системы могут отличаться от x₁, x₂, …, x_n. Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.

7. Общее решение неоднородной слау. Метод Гаусса рения слау. Вид общего решения неоднородной слау.

Решение систем линейных алгебраических уравнений общего вида. В общем случае число уравнений системы p не совпадает с числом неизвестных переменных n: Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная.

Прежде чем находить решение системы линейных уравнений необходимо установить ее совместность. Ответ на вопрос когда СЛАУ совместна, а когда несовместна, дает теорема Кронекера – Капелли: для того, чтобы система из p уравнений с n неизвестными (p может быть равно n) была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы, то есть, Rank(A) = Rank(T). Рассмотрим на примере применение теоремы Кронекера – Капелли для определения совместности системы линейных уравнений.

Пример. Выясните, имеет ли система линейных уравнений решения. Решение.

Найдем ранг основной матрицы системы . Воспользуемся методом окаймляющих миноров. Минор второго порядка отличен от нуля. Переберем окаймляющие его миноры третьего порядка: Так как все окаймляющие миноры третьего порядка равны нулю, то ранг основной матрицы равен двум. В свою очередь ранг расширенной матрицы равен трем, так как минор третьего порядка отличен от нуля. Таким образом, Rang(A) < Rang(T), следовательно, по теореме Кронекера – Капелли можно сделать вывод, что исходная система линейных уравнений несовместна. Ответ: система решений не имеет. Итак, мы научились устанавливать несовместность системы с помощью теоремы Кронекера – Капелли. А как же находить решение СЛАУ, если установлена ее совместность? Для этого нам потребуется понятие базисного минора матрицы и теорема о ранге матрицы. Минор наивысшего порядка матрицы А, отличный от нуля, называется базисным. Из определения базисного минора следует, что его порядок равен рангу матрицы. Для ненулевой матрицы А базисных миноров может быть несколько, один базисный минор есть всегда. Для примера рассмотрим матрицу . Все миноры третьего порядка этой матрицы равны нулю, так как элементы третьей строки этой матрицы представляют собой сумму соответствующих элементов первой и второй строк. Базисными являются следующие миноры второго порядка, так как они отличны от нуля Миноры базисными не являются, так как равны нулю.

Опишем алгоритм метода Гаусса. Пусть нам требуется решить систему из n линейных алгебраических уравнений с n неизвестными переменными вида , и пусть определитель ее основной матрицы отличен от нуля. Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x₁ из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид где , а . К такому же результату мы бы пришли, если бы выразили x₁ через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x₁ исключена из всех уравнений, начиная со второго. Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке Будем считать, что (в противном случае мы переставим местами вторую строку с k-ой, где ). Приступаем к исключению неизвестной переменной x₂ из всех уравнений, начиная с третьего. Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид где , а . Таким образом, переменная x₂ исключена из всех уравнений, начиная с третьего. Далее приступаем к исключению неизвестной x₃, при этом действуем аналогично с отмеченной на рисунке частью системы Так продолжаем прямой ход метода Гаусса пока система не примет вид 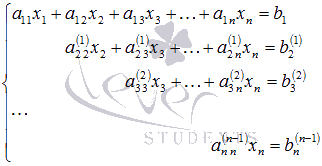С этого момента начинаем обратный ход метода Гаусса: вычисляем x_n из последнего уравнения как , с помощью полученного значения x_n находим x_n-1 из предпоследнего уравнения, и так далее, находим x₁ из первого уравнения.

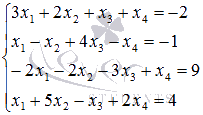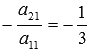Пример. Найдите решение системы уравнений методом Гаусса. Решение. Коэффициент a_{1 1} отличен от нуля, так что приступим к прямому ходу метода Гаусса, то есть, к исключению неизвестной переменной x₁ из всех уравнений системы, кроме первого. Для этого к левой и правой частям второго, третьего и четвертого уравнения прибавим левую и правую части первого уравнения, умноженные соответственно на , и : Неизвестную переменную x₁ исключили, переходим к исключению x₂. К левым и правым частям третьего и четвертого уравнений системы прибавляем левую и правую части второго уравнения, умноженные соответственно на и : Для завершения прямого хода метода Гаусса нам осталось исключить неизвестную переменную x₃ из последнего уравнения системы. Прибавим к левой и правой частям четвертого уравнения соответственно левую и правую часть третьего уравнения, умноженную на 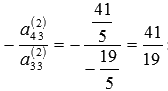: Можно начинать обратный ход метода Гаусса. Из последнего уравнения имеем , из третьего уравнения получаем , из второго , из первого 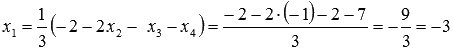. Для проверки можно подставить полученные значения неизвестных переменных в исходную систему уравнений. Все уравнения обращаются в тождества, что говорит о том, что решение по методу Гаусса найдено верно. Ответ: . А сейчас приведем решение этого же примера методом Гаусса в матричной форме записи. Расширенная матрица системы имеет вид . Сверху над каждым столбцом записаны неизвестные переменные, которым соответствуют элементы матрицы. Прямой ход метода Гаусса здесь предполагает приведение расширенной матрицы системы к трапецеидальному виду с помощью элементарных преобразований. Этот процесс схож с исключением неизвестных переменных, которое мы проводили с системой в координатной форме. Сейчас Вы в этом убедитесь. Преобразуем матрицу так, чтобы все элементы в первом столбце, начиная со второго, стали нулевыми. Для этого к элементам второй, третьей и четвертой строк прибавим соответствующие элементы первой строки умноженные на , и на соответственно: Далее полученную матрицу преобразуем так, чтобы во втором столбце все элементы, начиная с третьего стали нулевыми. Это будет соответствовать исключению неизвестной переменной x₂. Для этого к элементам третьей и четвертой строк прибавим соответствующие элементы первой строки матрицы, умноженные соответственно на и : Осталось исключить неизвестную переменную x₃ из последнего уравнения системы. Для этого к элементам последней строки полученной матрицы прибавим соответствующие элементы предпоследней строки, умноженные на : Следует отметить, что эта матрица соответствует системе линейных уравнений которая была получена ранее после прямого хода. Пришло время обратного хода. В матричной форме записи обратный ход метода Гаусса предполагает такое преобразование полученной матрицы, чтобы матрица, отмеченная на рисунке стала диагональной, то есть, приняла вид где - некоторые числа. Эти преобразования аналогичны преобразованиям прямого хода метода Гаусса, но выполняются не от первой строки к последней, а от последней к первой. Прибавим к элементам третьей, второй и первой строк соответствующие элементы последней строки, умноженные на , на и на соответственно: Теперь прибавим к элементам второй и первой строк соответствующие элементы третьей строки, умноженные на и на соответственно: На последнем шаге обратного хода метода Гаусса к элементам первой строки прибавляем соответствующие элементы второй строки, умноженные на : Полученная матрица соответствует системе уравнений , откуда находим неизвестные переменные. Ответ: .