
Общее определение машины; функциональная классификация машин (примеры).
О б щ е е о п р е д е л е н и е м а ш и н ы . Ф у н к ц и о н а л ь -н а я к л а с с и ф и к а ц и я м а ш и н . Машина есть устройство, создаваемое человеком для использования законов природы с целью облегчения физического и умственного труда, увеличения его производительности путем частичной или полной замены человека в его трудовых и физиологических функциях.
Все существующие машины можно разделить на следующие группы:
I. Энергетические. В них происходит преобразование энергии из одного вида в другой (например, электрогенераторы, электродвигатели, двигатели внутреннего сгорания любого типа, паровые и газовые турбины и т. д.).
II. Технологические. Они предназначены для изменения формы, размеров и физических свойств материалов (металлорежущие станки, деревообрабатывающие, дорожные, строительные, полиграфические машины, машины пищевых производств, машины текстильной и лёгкой промышленности и др.). Эти машины составляют самую многочисленную группу.
III. Транспортные. Эти машины служат для перемещения всевозможных изделий, материалов и людей (автомобили, самолёты, локомотивы, суда, подъемные краны, конвейеры, манипуляторы).
IV. Логические (информационные). Машины, составляющие эту группу, служат для хранения, переработки и передачи информации (различные вычислительные устройства, ЭВМ, компьютеры в том числе ПК).
V. Кибернетические. Для замены человека в его трудовых, и физиологических функциях (аппараты искусственное сердце, искусственные почки, робот-домохозяйка и др.).
ТММ изучает те машины и механизмы, которые функционируют на основе законов механики, отсюда другое название ТММ – механика машин
3.Классификация кинематических пар по различным признакам.
по виду места контакта (места связи) поверхностей звеньев:
низшие – в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения);
высшие – в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием)
по относительному движению звеньев, образующих пару:
вращательные;
поступательные;
винтовые;
плоские;
сферические.
по способу замыкания (обеспечения контакта звеньев пары):
силовое – за счет действия сил веса или упругости пружины;
геометрическое – за счет конструкции рабочих поверхностей пары).
по числу условий связи, накладываемых на относительное движение звеньев (число условий связи определяет класс кинематической пары);
по числу подвижностей в относительном движении звеньев.
Классификация КП по числу подвижностей и по числу связей приведена в таблице:

4. Классификация кинематических цепей
Кинематическая цепь – это система звеньев, связанных между собой кинематическими парами. Любой механизм представляет собой кинематическую цепь (к. ц.) звеньев, соединенных в кинематические пары (к.п.). К. ц. могут быть простыми и сложными, открытыми и замкнутыми, плоскими и пространственными. В простой к. ц. каждое из ее звеньев входит в состав одной или двух к. п., а в сложной к. ц. имеются звенья, входящие в состав трех и более к. п. В открытой к. ц. имеются звенья, входящие в состав одной к. п., а в замкнутой цепи каждое звено входит в состав 2-х и более к. п. (рис.6,а-в). Если точки всех звеньев двигаются в одной или параллельных плоскостях, то к. ц. называется плоской, в противном случае к. ц. – пространственная (точки звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые).

5. Расчёт степени подвижности плоского механизма (формула П.Л. Чебышёва).
Если в пространственной к. ц., состоящей из «n» подвижных звеньев, имеются к.п. 1-ого, 2-ого,… 5-ого класса, число которых, соответственно, p1,p2,… p5, то к. ц. имеет число степеней свободы, определяемое формулой А.П. Малышева.
W=6n-5p5-4p4-3p3-2p2-p1 (3.1)
Так как любой механизм имеет одно неподвижное звено (стойку) и «n» подвижных звеньев, то формула (3.1) может использоваться для определения W пространственного механизма, где n – число подвижных звеньев, а W – степень подвижности механизма, показывающая сколько нужно иметь ведущих звеньев (двигателей) для получения определенного движения остальных его звеньев.
Для плоского механизма степень подвижности определяется по формуле Чебышева:
W=3n-2p5-p4, (3.2)

При этом к.п. 5-ого класса существует в виде поступательных, вращательных и винтовых.
Например, кривошипно-ползунный плоский меха-низм (рис.7), в котором n=3; p5=4; p4=0,
имеет W=3·3-2·4-0=1.
При определении W необходимо учитывать возможность наличия так называемых «пассивных» звеньев, т.е. звеньев, устраняемых без формального ущерба для кинематики анализируемого механизма .
а) W=3·4-2·6-0=0 – с пассивным звеном,
б) W=3·3-2·4-0=1 – фактически.
Кроме того, необходимо учитывать возможность наличия избыточных связей, которые не реализуются в реальном механизме, а их число q определяется разностью между числом связей в к.п. действительного и формально возможного механизмов.
6.Избыточные (повторяющиеся) связи и местные подвижности в механизмах
Наряду
с движениями и условиями связей, которые
в механизме влияют на з акон
преобразования движения, могут
существовать такие связи и движения,
акон
преобразования движения, могут
существовать такие связи и движения,

Рисунок 1.8 Рисунок 1.9 которые не влияют на этот закон. Такие связи называются избыточными, а движения – местными подвижностями, или лишними степенями свободы. Одна избыточная связь уменьшает расчётную подвижность на единицу, а одна местная подвижность увеличивает её на единицу. На рис. 1.8 показан механизм шарнирного параллелограмма, у которого противоположные стороны попарно равны (отсюда его название). Расчёт подвижности этого механизма даёт Wрасч. = 3∙n – 2∙p5 = 3∙4 – 2∙6 = 0, что означает полное отсутствие движения звеньев, т. е. это не механизм, а ферма. Фактически же очевидно, что движение звеньев здесь возможно при ведущем, например звене 1, т. е. фактическая подвижность Wфакт.= 1. Звенья 2 и 4 выполняют одну и ту же функцию, передавая движение на звено 3, разделяя надвое общий силовой поток, снижая нагрузку, приходящуюся на каждое из них. С точки зрения структуры одно из этих звеньев (например, звено 4) можно считать избыточной связью. Если подсчитать подвижность кулачкового механизма (рис. 1.9), то окажется, что его Wрасч. = 2, т.е. в этом механизме должно быть два ведущих звена, что невозможно, так как W факт= 1. Местной подвижностью здесь является вращение ролика 2 относительно толкателя 3. Так как это движение не участвует в преобразовании движения в механизме, то оно является лишней степенью свободы. В данном случае это движение необходимо для замены трения скольжения трением качения, что является более выгодным с точки зрения потерь на трение (повышение КПД). При выполнении структурного анализа механизмов избыточные связи и местные подвижности должны быть исключены.
7.Замена высших пар в плоских механизмах.
При выполнении структурного анализа механизма, если в нём присутствуют высшие пары, требуется их заменить парами низшими. При этом необходимо выполнить следующие условия: 1) Количество связей, наложенных на относительное движение звеньев высшей пары заменяющей кинематической цепью должно остаться неизменным. 2) Мгновенное относительное движение звеньев высшей пары должно сохраниться. Для выполнения первого условия следует иметь в виду, что одна высшая пара накладывает одно условие связи, поэтому заменяющая кинематическая цепь должна также наложить одно условие связи. Отсюда вытекает равенство: 1 = 2 p5 – 3n, из которого следует p5 = (3n + 1)/2, что позволяет составить следующую табличку возможных сочетаний количества звеньев и пар заменяющей кинематической цепи
n |
1 |
3 |
… |
p5 |
2 |
5 |
… |
Таким
образом, в простейшем случае для замены
высшей пары требуется одно дополнительное
звено и две пары 5-го класса.
Для
выполнения второго условия необходимо
использовать следующую методику:
1)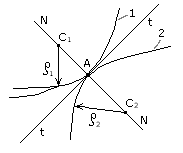 В точке контакта элементов высшей пары
провести нормаль N–N (Рис. 1.7).
2)
На нормали N–N определить положения
центров кривизны C1 элемента
1 и C2 элемента
2.
3)
В этих центрах поместить низшие пары
(5-го класса), а между ними условное
заменяющее звено.
Замечания. Если
один из элементов высшей пары заканчивается
острием, то в этом острие (в точке)
располагается одна из заменяющих низших
пар.
Рисунок
1.7 Если одно из звеньев высшей пары в
зоне контак- та имеет форму прямой линии,
то в этом месте пара 5-го класса должна
быть поступательной.
В точке контакта элементов высшей пары
провести нормаль N–N (Рис. 1.7).
2)
На нормали N–N определить положения
центров кривизны C1 элемента
1 и C2 элемента
2.
3)
В этих центрах поместить низшие пары
(5-го класса), а между ними условное
заменяющее звено.
Замечания. Если
один из элементов высшей пары заканчивается
острием, то в этом острие (в точке)
располагается одна из заменяющих низших
пар.
Рисунок
1.7 Если одно из звеньев высшей пары в
зоне контак- та имеет форму прямой линии,
то в этом месте пара 5-го класса должна
быть поступательной.
8.Структурная классификация плоских механизмов; формула строения
Принцип
структурного образования механизмов
по Л.В. Ассуру
Основы
теории структуры плоских механизмов
были заложены в 1914 г. профессором Л.В.
Ассуром. Согласно сформулированному
им принципу, любой плоск ий
механизм (рис. 1.6) может быть образован
путем присоединения к исходному
механизму, включающему стойку и ведущее
звено, кинематических цепей, имеющих
нулевую подвижность. Тогда подвижность
механизма запишется как сумма
Wмех =
Wисх. мех + 0 + 0 + 0 +
…
Группы
Ассура и их классификация
Кинематическая
цепь, которая после присоединения её
всеми свободными элементами кинематических
пар к стойке получает подвижность,
равную нулю, называется группой Асура.
Таким образом,
Wгр.Асс. =
0.
В
состав группы Асура входят только
кинематические пары 5 класса, поэтому,
согласно формуле Чебышёва:
Wгр.Асс. =
3n – 2 p5 =
0,
откуда
получаем 3n
= 2p5 , или p5 =
3/2∙n,
как условие существования группы
Ас-
сура.
Составим таблицу из нескольких сочетаний
количества звеньев и кинематических
пар в группах Ассура согласно приведённому
выше соотношению
ий
механизм (рис. 1.6) может быть образован
путем присоединения к исходному
механизму, включающему стойку и ведущее
звено, кинематических цепей, имеющих
нулевую подвижность. Тогда подвижность
механизма запишется как сумма
Wмех =
Wисх. мех + 0 + 0 + 0 +
…
Группы
Ассура и их классификация
Кинематическая
цепь, которая после присоединения её
всеми свободными элементами кинематических
пар к стойке получает подвижность,
равную нулю, называется группой Асура.
Таким образом,
Wгр.Асс. =
0.
В
состав группы Асура входят только
кинематические пары 5 класса, поэтому,
согласно формуле Чебышёва:
Wгр.Асс. =
3n – 2 p5 =
0,
откуда
получаем 3n
= 2p5 , или p5 =
3/2∙n,
как условие существования группы
Ас-
сура.
Составим таблицу из нескольких сочетаний
количества звеньев и кинематических
пар в группах Ассура согласно приведённому
выше соотношению
n |
2 |
4 |
6… |
p5 |
3 |
6 |
9… |
Группы
Ассура делятся на классы и порядки.
Класс
группы определяется классом наиболее
сложного замкнутого контура в составе
группы:
![]()
![]()
![]()
![]()
II
класс III класс IV класс V класс и т.
д.
Кинематические
пары в контуре III класса, могут быть
расположены по одной прямой, не образуя
никакой контур, однако считается, что
и в этом случае имеется контур III класса.
Порядок групп Ассура определяется
количеством свободных элементов
кинематических пар, которыми группы
Ассура присоединяются к други м
звеньям.
Рассмотрим
несколько примеров групп Ассура и
механизмов с этими группами.
м
звеньям.
Рассмотрим
несколько примеров групп Ассура и
механизмов с этими группами.
![]()

![]() Группа
Ассура II класса, 2-го порядка
Четырёхшарнирный
1-го
вида механизм
Группы
II класса делятся также на виды (модификации)
в зависимости от количества и расположения
в них поступательных и вращательных
кинематических
пар.
Приведённая выше группа Ассура относится
к первому
виду. Если
в этой группе один из крайних элементов
вращательной пары заменить поступательным,
то получится группа второго
вида.
Если заменить среднюю вращательную
пару поступательной, то такая группа
Ассура получится группой Ассура третьего
вида.
Группа
Ассура II класса, 2-го порядка
Четырёхшарнирный
1-го
вида механизм
Группы
II класса делятся также на виды (модификации)
в зависимости от количества и расположения
в них поступательных и вращательных
кинематических
пар.
Приведённая выше группа Ассура относится
к первому
виду. Если
в этой группе один из крайних элементов
вращательной пары заменить поступательным,
то получится группа второго
вида.
Если заменить среднюю вращательную
пару поступательной, то такая группа
Ассура получится группой Ассура третьего
вида.
 Группа
Ассура Кривошипно-ползунный
II
класса, 2-го механизм
порядка,
2-го вида
Группа
Ассура Кривошипно-ползунный
II
класса, 2-го механизм
порядка,
2-го вида

 Группа
Ассура II класса, Кривошипно-кулисный
2-го
порядка, 3-го вида механизм
n
Группа
Ассура II класса, Кривошипно-кулисный
2-го
порядка, 3-го вида механизм
n
 = 4
p5 =
6
Группа
Ассура III класса, Группа Ассура IV
класса
3-го
порядка 4-го порядка
= 4
p5 =
6
Группа
Ассура III класса, Группа Ассура IV
класса
3-го
порядка 4-го порядка
Формула
строения отражает порядок присоединения
групп Ассура друг к другу и к исходному
механизму. Приведём здесь для примера
вид формулы строения двух механизмов
безотносительно к их кинематическим
схемам:
При
одном ведущем звене При двух ведущих
звеньях


10. Кинематические характеристики механизмов.
Основным назначением механизма является выполнение
им требуемых движений. Эти движения могут быть описа-
ны посредствам его кинематических характеристик. К ним
относят координаты точек и звеньев, их траектории, ско-
рости и ускорения. К числу кинематических характеристик
относятся и такие характеристики, которые не зависят от
закона движения начальных звеньев, определяются только
строением механизма и размерами его звеньев и в общем
случае зависят от обобщенных координат. Это функции
положения, кинематические передаточные функции ско-
рости и ускорения.
Для создания механизмов, наилучшим образом отвеча-
ющих поставленным требованиям, надо знать методы опре-
деления кинематических характеристик механизмов.
Различают следующие методы определения кинемати-
ческих характеристик механизмов.
1. Геометрический метод — основанный на анализе век-
торных контуров кинематических цепей механизмов, пред-
ставленных в аналитическом или графическом виде.
2. Метод преобразования координат точек механизма,
решаемый в матричной или тензорной форме (обычно при-
меняется для исследования кинематических цепей манипу-
ляторов промышленных роботов с использованием ЭВМ).
3. Метод кинематических диаграмм — метод числен-
ного интегрирования и дифференцирования (решаемый с
помощью ЭВМ или графически).
4. Метод планов положений, скоростей и ускорений,
основанный на решении векторных уравнений, связыва-
ющих кинематические параметры, в графическом виде или
аналитической форме.
5. Экспериментальный метод.
11. .Задачи кинематического анализа; исходные данные; методы анализа.
Кинематический анализ механизма – исследование его основных параметров с целью изучения законов изменения и на основе этого выбор из ряда известных наилучшего механизма. По сравнению с синтезом анализ механизма широко используется в практике.
Кинематический анализ механизма выполняется либо для заданного момента времени, либо для заданного положения входного звена; иногда для анализируемого положения механизма задают взаимное расположение каких-либо его звеньев.
Цели:
1. Определение кинематических характеристик звеньев: перемещение; скорость; ускорение; траектория движения; функция положения при известных законах движения входных (ведущих) звеньев.
2. Оценка кинематических условий работы рабочего (выходного) звена.
3. Определение необходимых численных данных для проведения силового, динамического, энергетического и других расчётов механизма.
Исходные данные:
1. Кинематическая схема механизма.
2. Размеры и иные геометрические параметры звеньев (но только такие, которые не изменяются при движении механизма).
3. Законы движения входных звеньев (или параметры движения, например, угловая скорость и угловое ускорение входного звена в выбранном для анализа положении механизма).
Для механизмов, подчиняющихся классификации Л. В. Ассура, порядок кинематического анализа определяется формулой строения: вначале находят параметры движения начальных механизмов и затем – структурных групп в порядке следования их в формуле строения. Здесь следует руководствоваться простым правилом: кинематика любого элемента формулы строения может быть изучена только после того, как она изучена для всех предшествующих в этой формуле элементов.
Методы:
- графический (или метод графиков и диаграмм);
- графоаналитический (или метод планов скоростей и ускорений);
- аналитический;
- экспериментальный.
Графический метод кинематического анализа
Преимущество этого метода заключается в наглядности и простоте. Он хорош для кинематического анализа звеньев, совершающих возвратно-поступательное движение. Недостаток метода – невысокая точность, которая зависит от точности графических построений.
Графоаналитический метод кинематического анализа
Графоаналитический метод называют методом планов скоростей и ускорений.
Графический (метод диаграмм) и графоаналитический методы (метод планов скоростей и ускорений) кинематического анализа механизмов имеют недостатки: невысокая точность, определяемая точностью графических построений, и большая трудоёмкость. При иcпользовании графического метода необходимо построить диаграммы перемещений, скоростей и ускорений для каждой исследуемой точки механизма, а при использовании графоаналитического метода – несколько планов скоростей и ускорений механизма, чтобы определить динамику изменения скорости и ускорения интересующих нас точек (т.е. при различных положениях механизма).
Эти недостатки отсутствуют в аналитическом методе. Но при этом необходимо составлять достаточно сложные аналитические зависимости (формулы) и иметь возможность решать их с использованием компьютерных техники и технологии, что в последнее время возможно и доступно.
Методы аналитического исследования:
метод замкнутых векторных контуров (метод Зиновьева) удобен для кинематического анализа практически всех используемых в технике несложных рычажных механизмов;
метод преобразования координат (метод Морошкина) удобен для кинематического анализа многозвенных механизмов типа манипуляторов промышленных роботов.
12. Аналитический метод исследования кинематики механизма (на примере синусного механизма).
Аналитические
методы исследования позволяют проводить
анализ с заданной степенью точности.
Кроме того, создание математических
моделей механизмов позволяет решать
задачи их оптимального синтеза при
использовании ЭВМ.
 Рассмотрим
пример кинематического исследования
синусного механизма (механизм двойного
ползуна), где кривошип 1 вращается с
угловой скоростью ω и угловым ускорением
ε (рис.20).
Тогда
скорость и ускорение точки А
равны:
VA=lOA·ω;
Рассмотрим
пример кинематического исследования
синусного механизма (механизм двойного
ползуна), где кривошип 1 вращается с
угловой скоростью ω и угловым ускорением
ε (рис.20).
Тогда
скорость и ускорение точки А
равны:
VA=lOA·ω; ![]() .
Все
точки звена 1 и 2 описывают окружности,
а точки звена 3 движутся поступательно,
имея перемещения, скорости и ускорения
равные:
SB=lOA·sinφ=lOA·sinωt;
VB=dSB/dt=dSB·dφ/dφ·dt=lOA·ω·cosφ;
aB=d2SB/dt=lOA·(ε·cosφ-ω2·sinφ)
при
ε=0 aB=-lOA·ω2·sinφ.
При
исследовании многих механизмов получаются
достаточно громоздкие формулы, что не
является препятствием при использовании
ЭВМ.
При
исследовании пространственных механизмов
используются элементы векторной алгебры
и векторного анализа. Положения, скорости
и ускорения точек механизма выражаются
в векторной форме, при необходимости
вычисляются проекции на оси и плоскости.
.
Все
точки звена 1 и 2 описывают окружности,
а точки звена 3 движутся поступательно,
имея перемещения, скорости и ускорения
равные:
SB=lOA·sinφ=lOA·sinωt;
VB=dSB/dt=dSB·dφ/dφ·dt=lOA·ω·cosφ;
aB=d2SB/dt=lOA·(ε·cosφ-ω2·sinφ)
при
ε=0 aB=-lOA·ω2·sinφ.
При
исследовании многих механизмов получаются
достаточно громоздкие формулы, что не
является препятствием при использовании
ЭВМ.
При
исследовании пространственных механизмов
используются элементы векторной алгебры
и векторного анализа. Положения, скорости
и ускорения точек механизма выражаются
в векторной форме, при необходимости
вычисляются проекции на оси и плоскости.
13. Определение функции положения механизма с помощью разметки
Определение
функции положения
При
использовании графоаналитического
метода определение функции положения
механизма производится с помощью
разметки механизма. Разметка
механизма –
это ряд последовательных положений
механизма, построенный в зависимости
от положений входного звена, охватывающих
весь цикл его движения (как правило,
один оборот). Каждый механизм в соответствии
с его кинематической схемой имеет свои
особенности в построении разметки.
Разметка строится в некотором масштабе,
начиная от одного из крайних по ложений,
отмечаемого нулевым номером. Затем
окружность, описываемая концом входного
звена (кривошипа), делится на двенадцать
равных частей, которые обозначаются
номерами в направлении угловой скорости.
После этого строятся положения остальных
звеньев механизма, и строятся траектории
заданных точек.
Для
примера на рис. 4.2 приведена разметка
кривошипно – ползунного механизма, с
помощью которой легко определить путём
измерений перемещения точки В ведомого
звена, соответствующие углам поворота
кривошипа, и представить их в виде
графика или таблицы. Это и будет функция
положения механизма.
З
а м е ч а н и е о м а с ш т а б е . Масштабом
называется число, показывающее, сколько
единиц физической величины содержится
в одном миллиметре её изображения. В
механике машин в масштабе изображаются
любые физические величины: угол поворота,
время, перемещение, скорость, сила,
работа, мощность и т. д. Масштаб обозначается
буквой
ложений,
отмечаемого нулевым номером. Затем
окружность, описываемая концом входного
звена (кривошипа), делится на двенадцать
равных частей, которые обозначаются
номерами в направлении угловой скорости.
После этого строятся положения остальных
звеньев механизма, и строятся траектории
заданных точек.
Для
примера на рис. 4.2 приведена разметка
кривошипно – ползунного механизма, с
помощью которой легко определить путём
измерений перемещения точки В ведомого
звена, соответствующие углам поворота
кривошипа, и представить их в виде
графика или таблицы. Это и будет функция
положения механизма.
З
а м е ч а н и е о м а с ш т а б е . Масштабом
называется число, показывающее, сколько
единиц физической величины содержится
в одном миллиметре её изображения. В
механике машин в масштабе изображаются
любые физические величины: угол поворота,
время, перемещение, скорость, сила,
работа, мощность и т. д. Масштаб обозначается
буквой ![]() с
индексом обозначения физической величины
и имеет размерность в виде дроби, в
числителе которой указывается размерность
изображаемой физической величины, в
знаменателе – миллиметры. Например:
с
индексом обозначения физической величины
и имеет размерность в виде дроби, в
числителе которой указывается размерность
изображаемой физической величины, в
знаменателе – миллиметры. Например:  –
масштаб длин читается: ноль целых, две
тысячных метра в одном миллиметре
(изображения);
–
масштаб длин читается: ноль целых, две
тысячных метра в одном миллиметре
(изображения);  –
масштаб времени, читается: две секунды
в одном миллиметре.
–
масштаб времени, читается: две секунды
в одном миллиметре.
14. Определение скоростей и ускорений механизма с группой Ассура 2-го вида методом планов.
Планом скоростей (ускорений) механизма называется пучок векторов, выходящих из одной точки (полюса плана), каждый из которых в некотором масштабе изображает вектор абсолютной скорости (абсолютного ускорения) какой-либо точки механизма, а отрезки, соединяющие их концы, изображают векторы относительных скоростей (относительных ускорений).

Построение плана скоростей сводится к реализации известного положения теоретической механики, согласно которому при плоско-параллельном движении твёрдого тела (звена) скорость любой его точки равна векторной сумме скорости в поступательном переносном движении вместе с другой точкой, принятой в качестве полюса, и скорости её в относительном вращательном движении относительно этого полюса.
Р
ассмотрим построение планов скоростей и ускорений на примере кривошипно-ползунного механизма (рис. 4.3). Схема механизма должна быть изображена в масштабе
 в исследуемом положении. Прежде необходимо
определить параметры движения точки
А. Её скорость по величине равна
произведению угловой скорости
в исследуемом положении. Прежде необходимо
определить параметры движения точки
А. Её скорость по величине равна
произведению угловой скорости
 кривошипа 1 на его радиус
кривошипа 1 на его радиус
 ,
т. е.
,
т. е.
 и направлена перпендикулярно кривошипу
в сторону движения точки А. Ускорение
точки А по величине равно произведению
квадрата угловой скорости кривошипа
также на его радиус, т. е.
и направлена перпендикулярно кривошипу
в сторону движения точки А. Ускорение
точки А по величине равно произведению
квадрата угловой скорости кривошипа
также на его радиус, т. е.
 и направлено от точки А к точке О, так
как совпадает с нормальной составляющей
полного ускорения точки А из-за равенства
нулю тангенциальной составляющей
ускорения (угловое ускорение кривошипа
принимается равным нулю). Точка А
принадлежит не только кривошипу, но и
шатуну 2 и принимается в качестве полюса
относительного вращения точки В. Скорость
точки В определяется векторным равенством
и направлено от точки А к точке О, так
как совпадает с нормальной составляющей
полного ускорения точки А из-за равенства
нулю тангенциальной составляющей
ускорения (угловое ускорение кривошипа
принимается равным нулю). Точка А
принадлежит не только кривошипу, но и
шатуну 2 и принимается в качестве полюса
относительного вращения точки В. Скорость
точки В определяется векторным равенством
 ,
т. е. скорость точки В равна скорости
точки А плюс скорость точки В относительно
точки А. В этом равенстве первое слагаемое
правой части известно по величине и по
направлению, второе слагаемое направлено
перпендикулярно шатуну 2 в данном
положении, т. е. известно по направлению,
и, наконец, вектор левой части направлен
параллельно направляющим ползуна. При
этих условиях треугольник скоростей
легко строится в предварительно выбранном
масштабе
,
т. е. скорость точки В равна скорости
точки А плюс скорость точки В относительно
точки А. В этом равенстве первое слагаемое
правой части известно по величине и по
направлению, второе слагаемое направлено
перпендикулярно шатуну 2 в данном
положении, т. е. известно по направлению,
и, наконец, вектор левой части направлен
параллельно направляющим ползуна. При
этих условиях треугольник скоростей
легко строится в предварительно выбранном
масштабе
 .
.
Построение
плана ускорений производится в той же
последовательности, что и план скоростей.
При этом используется векторное равенство
 ,
в котором первый вектор правой части
известен полностью, второй неизвестен
ни по величине, ни по направлению. Вектор
левой части известен по направлению –
он направлен параллельно направляющим
ползуна. В этих условиях треугольник
ускорений не строится. Разложим вектор
относительного ускорения на две
составляющих, согласно равенству
,
в котором первый вектор правой части
известен полностью, второй неизвестен
ни по величине, ни по направлению. Вектор
левой части известен по направлению –
он направлен параллельно направляющим
ползуна. В этих условиях треугольник
ускорений не строится. Разложим вектор
относительного ускорения на две
составляющих, согласно равенству
 .
Первое слагаемое представляет собой
относительное нормальное ускорение,
направленное от точки В к точке А и
равное по величине частному от деления
квадрата относительной скорости на
длину шатуна, т. е.
.
Первое слагаемое представляет собой
относительное нормальное ускорение,
направленное от точки В к точке А и
равное по величине частному от деления
квадрата относительной скорости на
длину шатуна, т. е.
 .
Второе слагаемое, относительное
тангенциальное ускорение направлено
перпендикулярно шатуну 2 и неизвестно
по величине. Теперь план ускорений
строится без затруднений с применением
заранее выбранного масштаба
.
Второе слагаемое, относительное
тангенциальное ускорение направлено
перпендикулярно шатуну 2 и неизвестно
по величине. Теперь план ускорений
строится без затруднений с применением
заранее выбранного масштаба
 .
Планы скоростей и ускорений данного
механизма представлены на рис. 4.3.
.
Планы скоростей и ускорений данного
механизма представлены на рис. 4.3.
Используя планы, легко найти физические величины скоростей и ускорений, для этого необходимо измерить отрезки в миллиметрах, выражающие скорости и ускорения, и умножить их на соответствующий масштаб.
Абсолютная
скорость точки В:
 ,
,
 .
.
Относительная
скорость точки В:
 ,
.
,
.
Угловая
скорость шатуна 2:
 ,
,
 .
.
Тангенциальное ускорения точки В относительно точки А:
 ,
,
 .
.
Полное
относительное ускорение:
 ,
.
,
.
Угловое
ускорение шатуна 2:
 ,
,
 .
.
15.14.16. Определение скоростей и ускорений механизма с группой Ассура 1-го вида методом планов. Определение скоростей и ускорений механизма с группой Ассура 2-го вида методом планов. Определение скоростей и ускорений механизма с группой Ассура 2-го класса методом планов
Кинематическое исследование механизма методом планов скоростей и ускорений
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:
![]()
На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.
На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.

Рисунок 1 – Кинематическая схема плоского рычажного механизма
Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения. Начальный механизм:
![]()
Здесь
![]()
По вычисленному значению VA выбираем масштаб плана скоростей KV и из произвольного полюса откладываем отрезок va изображающий эту скорость:

Можно также назначать отрезок va а масштаб KV вычислять:

Группа Ассура второго класса 1-го вида (звенья 2, 3):

Истинные значения (в м/с) относительных скоростей VBA и VBC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:

а зная их, можно определить и угловые скорости звеньев 2 и 3:

Скорость точки D на плане скоростей можно определить по подобию. (Если известны скорости двух точек одного и того же звена, то скорость любой третьей точки этого же звена можно определить, построив на плане скоростей фигуру, подобную фигуре, образованной этими же буквами на звене механизма). Точки С, В , D на звене 3 лежат на одной прямой. На плане строим отрезок сd, соблюдая условие подобия:

Группа Ассура второго класса 3- го вида (звенья 4,5) :

где D5 - точка, находящаяся на звене 5 под точкой D. После определения скорости движения точки D5 относительно точки E можно вычислить угловую скорость звеньев 4 и 5 ( ω4= ω5, т. к. эти звенья соединяются поступательной парой):

Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.
План ускорений строится в таком же порядке.
Начальный механизм
Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена ( ω1=соnst):
![]()
По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):

Здесь точка w – полюс плана ускорений.
Группа Ассура (звенья 2,3) второго класса 1-го вида:

После построения определяются aτBA и aτBC, по которым можно вычислить угловые ускорения звеньев 2 и 3:

Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:


Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма
Группа Ассура (звенья 4,5) второго класса 3-го вида:

Для определения направления akD5D надо вектор VD5D повернуть на 900 в направлении ω5. Угловые ускорения:

При силовом расчете необходимо иметь ускорения центров масс ( asi ), которые на плане ускорений определяются методом подобия.
Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.
Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.
Таблица 1 – Кинематический анализ групп Ассура II класса методом планов
Вид группы |
Конфигурация группы
|
Уравнения для построения планов скоростей и для определения угловых скоростей |
Уравнения для построения планов ускорений и для определения угловых ускорений |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
17. Метод графического дифференцирования при исследовании кинематики механизмов.
Метод касательных основан на геометрической интерпретации производной. При использовании метода кинематических диаграмм вначале дифференцируется диаграмма перемещений для получения графика (диаграммы) скоростей. Рассмотрим графическое дифференцирование на этом примере.
V = ds/dt, но т.к. аналитическое выражение для перемещений в данном случае отсутствует, то представляем значения перемещений и времени через отрезки на диаграмме перемещений:
![]()
тогда

Но отношение бесконечно малого приращения функции к бесконечно малому приращению аргумента на графике представляет собой тангенс угла наклона касательной к данной кривой в рассматриваемой точке, т.е.
![]()
Используя данное обстоятельство, диаграмму скоростей строят в следующем порядке (рисунок 11):
- проводят касательные к диаграмме перемещений в намеченных положениях;
- слева от начала координат на оси абсцисс будущей диаграммы скоростей отмечают полюс P на некотором расстоянии H (которое называется полюсным расстоянием);
- из полюса проводят лучи, параллельные проведенным касательным на диаграмме перемещений. Эти лучи отсекают на оси ординат будущей диаграммы скоростей отрезки
oi*=H.tg α
Таким образом, и скорость в i-том положении и отрезки oi* пропорциональны tg α , а значит отрезкиoi* пропорциональны Vi ( скорости исследуемого звена в соответствующем положении механизма), т.е. они представляют собой
__
изображение скорости в виде отрезка в некотором масштабе – Vi .
![]()
или

т.е.

где Kv – масштаб диаграммы скоростей по оси ординат в (м/с)/мм.
Далее отрезки oi* переносят в соответствующие положения, отмеченные на оси абсцисс, и, соединив концы отрезков плавной кривой, получают диаграмму скоростей исследуемого звена. Аналогично строится диаграмма ускорений. При этом масштаб ускорений


Рисунок 11
Теоретически метод касательных самый точный из графических методов дифференцирования, т.к. дает значение мгновенной скорости (ускорения) именно в том положении, в котором проведена касательная.
Однако из-за трудности точного проведения касательных (и сама дифференцируемая кривая, построенная по точкам, имеет отклонения от ее теоретической функции), практическая точность этого метода весьма низкая, поэтому он используется редко (обычно когда надо проанализировать характер движения звена без получения конкретных численных результатов).
18. Задачи кинетостатики на примере любого механизма; исходные данные.
Кинетостатика механизмов
Кинетостатика механизмов
раздел теории машин и механизмов, в котором методом так называемого силового расчёта определяют реакции элементов кинематических пар механизма при условии, что закон его движения известен (см. Машин и механизмов теория). Методами К. м. пользуются при проектировании новых машин для расчётов их на прочность.
Если
ко всем внешним силам, приложенным к
звеньям механизма, добавить силы инерции,
то на основании Д'Аламбера принципа
весь механизм в целом и отдельные его
части условно можно рассматривать
находящимися в состоянии равновесия.
Поэтому при определении сил, действующих
на механизм (реакций), пользуются
уравнениями статики (см. Статика
механизмов).
Системы уравнений составляют для частей
механизма — звеньев и кинематических
пар. Число неизвестных реакций равно
числу уравнений. Подобные системы в
механике называют статически определимыми.
Силовой расчёт механизма ведут
последовательно для кинематических
пар, начиная с группы, наиболее удалённой
от начального звена механизма. Например,
механизм (рис.,
а) состоит из начального звена 1 и
кинематических пар, содержащих
звенья 2—3 и 4—5. К
звеньям приложены силы P1, Р2,
Р3,
Р4, включая
инерционные нагрузки, и моменты M1,
М2,
M5. Для
силового расчёта рассматривают вначале
группу 4—5 механизма
(рис.,
б). Действие звеньев 6 и 2 на
группу заменяют искомыми реакциямиP24 и P65,
которые разлагаются на нормальные
составляющие ![]() n24 и p̅n65 и
тангенциальные составляющие p̅τ24 и
P̅τ65.
Тангенциальные составляющие определяются
из уравнений сумм моментов относительно
точки Е для
каждого из звеньев 4 и 5. Нормальные
составляющие P̅n24 и
P̅n65,
а следовательно, и полные
реакции P24 и P65 определяют
из векторного уравнения равновесия
группы
n24 и p̅n65 и
тангенциальные составляющие p̅τ24 и
P̅τ65.
Тангенциальные составляющие определяются
из уравнений сумм моментов относительно
точки Е для
каждого из звеньев 4 и 5. Нормальные
составляющие P̅n24 и
P̅n65,
а следовательно, и полные
реакции P24 и P65 определяют
из векторного уравнения равновесия
группы
ρ̅4 + ρ̅τ24 + ρ̅n24 + ρ̅n65 + ρ̅τ65 = 0
Для решения векторного уравнения строят многоугольник сил (см. Верёвочный многоугольник). Реакцию P̅45 = —P̅54 определяют из векторного уравнения равновесия сил на одном из звеньев 4 или 5. Затем рассматривают группу 2—3, на которую, кроме заданных сил, действует найденная реакция P̅42 = —p̅24. При рассмотрении равновесия начального звена 1 определяют реакцию P̅61 и уравновешивающий момент My, приложенный к этому звену, необходимый для обеспечения заданного закона движения начального звена.
При учёте сил трения в кинематических парах к системе уравнений добавляют ещё одно независимое уравнение. После определения реакций вычисляют силы трения в парах и повторяют расчет, принимая во внимание силы трения как внешние силы, приложенные к звеньям, то есть находят уточненные реакции в первом приближении. Расчет можно повторить с учетом определенных сил трения. Практически первого приближения бывает достаточно. При силовом расчёте многозвенных пространственных механизмов метод и последовательность кинетостатического исследования сохраняются, однако решение получается более громоздким.
Лит. см. при ст. Машин и механизмов теория.
И. И. Артоболевский, А. П. Бессонов.

Схема действия сил в механизме (а) и определение реакций в звене (б); P1, P2, P3, P4 — действующие силы; M1, М2, M5, — моменты сил; Р24 и Р65 — искомые реакции.
19. Расчёт сил инерции.
Расчёт сил инерции относится к предварительному расчёту, предшествующему основной задаче определения реакций в кинематических парах.
Силы инерции возникают во всех случаях, когда звенья движутся непрямолинейно и/или неравномерно. Рассмотрим три вида движения звеньев.
Поступательное движение звена
Этот
вид движения чаще всего относится к
ползунам, движущимся относительно
прямолинейных направляющих (рис. 5.1).
Пусть при этом
 –это
масса ползуна,
–это
масса ползуна,
 –
его ускорение.
–
его ускорение.
С ила
инерции элементарной массы звена
ила
инерции элементарной массы звена
 .
Если просуммировать все элементарные
силы инерции данного ползуна, т. е. найти
сумму
.
Если просуммировать все элементарные
силы инерции данного ползуна, т. е. найти
сумму
 ,
то получится главный вектор сил инерции
звена, равный
,
то получится главный вектор сил инерции
звена, равный
 .
То есть главный вектор сил инерции, или
просто сила
инерции звена в его поступательном
движении равна массе звена, помноженной
на его ускорение.
Знак «минус» в правой части формулы
указывает на противоположность
направления силы инерции по отношению
к ускорению.
.
То есть главный вектор сил инерции, или
просто сила
инерции звена в его поступательном
движении равна массе звена, помноженной
на его ускорение.
Знак «минус» в правой части формулы
указывает на противоположность
направления силы инерции по отношению
к ускорению.
Вращательное движение звена
В этом движении находятся кривошипы, кулисы, коромысла и другие звенья механизмов. Возьмём стержневое звено ОА (рис. 5.2), вращающееся вокруг неподвижной точки О.
Масса
звена равна
,
момент инерции относительно центра
масс S
равен
 .
Вращение происходит с угловой скоростью
.
Вращение происходит с угловой скоростью
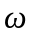 и угловым ускорением
и угловым ускорением
 .
Расстояние между центром масс и центром
вращения равно
.
Расстояние между центром масс и центром
вращения равно
 .
.
Вычислим
ускорение, с которым движется центр
масс S.
Его нормальное ускорение равно
 ,
тангенциальное ускорение равно
,
тангенциальное ускорение равно
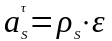 .
Так как эти составляющие полного
ускорения перпендикулярны друг другу,
то полное ускорение равно
.
Так как эти составляющие полного
ускорения перпендикулярны друг другу,
то полное ускорение равно
 .
В
.
В результате наличия этого ускорения
возникает сила инерции, приложенная в
центре масс, направленная противоположно
ускорению центра масс
результате наличия этого ускорения
возникает сила инерции, приложенная в
центре масс, направленная противоположно
ускорению центра масс
 .
.
Угловое ускорение звена вызывает появление инерционного момента (или момента сил инерции), направленного по отношению к нему в противоположную сторону
 .
.
В
этой формуле момент инерции принимается
относительно центра вращения и
определяется формулой
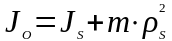 .
.
Частные случаи
1.
 .
2.
.
2.
 .
.
3.
 .
.
Плоско-параллельное движение звена
Такое
движение совершают чаще всего шатуны
механизмов. На рис. 5.3 изображён шатун,
совершающий такое движение. Масса шатуна
равна
,
момент и нерции
относительно центра масс равен
.
нерции
относительно центра масс равен
.
Звено
движется, имея угловое ускорение
и ускорение центра
масс
 .
Аналогично вращательному движению в
этом случае также будут действовать
оба инерционных фактора: сила инерции
.
Аналогично вращательному движению в
этом случае также будут действовать
оба инерционных фактора: сила инерции
 ,
противоположная ускорению, и момент
сил инерции
,
противоположная ускорению, и момент
сил инерции
 ,
противоположный угловому ускорению
,
противоположный угловому ускорению
20. Общие положения силового расчета механизмов (принцип Даламбера, принцип освобождаемости, статическая определимость групп Ассура, порядок силового расчёта механизма).
Принцип Даламбера
Силовой расчёт механизмов выполняется на основе принципа Даламбера, позволяющего рассматривать подвижные системы, к которым относятся механизмы, как неподвижные, находящиеся в равновесии. Принцип Даламбера можно сформулировать так: если к системе сил, действующих на подвижную систему, добавить силы инерции, то такую систему можно рассматривать как находящуюся в равновесии, и к ней применимы законы статики.















