
- •2.1.3. Необходимое и достаточное условие линейной зависимости системы векторов
- •2.1.4. Необходимое условие линейной независимости системы векторов (в координатах)
- •2.2. Размерность пространства Rn. Базис в Rn
- •2.2.1. Свойства базиса, естественный базис, координаты вектора в заданном базисе
- •Нахождение собственных чисел и собственных векторов матриц
- •14.1. Определение евклидова пространства и его примеры
- •§ 7. Ортонормированный базис
- •1.4.3. Тригонометрическая форма записи комплексных чисел
- •Геометрический метод решения задачи линейного программирования
Лекция 6. Раздел 6.3 Базисный минор и ранг матрицы.
Введя понятие линейной комбинации строк и столбцов матрицы, как это было сделано у векторов, можно ввести понятие их линейной зависимости и независимости.
Определение
6.3.1. Строки ![]() ,
,![]() ,...,
,..., ![]() называются
линейно зависимыми, если существуют
такие числа
называются
линейно зависимыми, если существуют
такие числа ![]() ,
не все равные нулю, что справедливо
равенство
,
не все равные нулю, что справедливо
равенство ![]() .
.
Здесь 0 – нулевая строка.
Определение
6.3.2. Строки ![]() называются
линейно независимыми, если их линейная
комбинация обращается в ноль лишь при
условии, что
называются
линейно независимыми, если их линейная
комбинация обращается в ноль лишь при
условии, что ![]() .
.
В этом случае линейная комбинация называется тривиальной.
Так же как и у векторов имеется соответствующая теорема.
Теорема 6.3.1. Для того чтобы строки были линейно зависимы, необходимо и достаточно, чтобы одна из них была линейной комбинацией остальных.
Доказательство проводится так же, как и в п. 1.4.
Теорема 6.3.2. Если в систему строк матрицы входит нулевая строка, то эти строки линейно зависимы.
Доказательство. Действительно, нулевая строка представляет собой тривиальную линейную комбинацию любых строк. Но тогда мы сразу переходим к теореме 1.
Рассмотрим
теперь понятие базисного минора. Пусть
имеется произвольная матрица порядка ![]() :
:
 .
.
Определение
6.3.3. Минором ![]() -го
порядка матрицы
-го
порядка матрицы ![]() называется
определитель
-го
порядка с элементами, лежащими на
пересечении любых
строк
и
столбцов
матрицы
.
называется
определитель
-го
порядка с элементами, лежащими на
пересечении любых
строк
и
столбцов
матрицы
.
Определение
6.3.4. В
матрице
,
порядка
,
минор порядка ![]() называется
базисным, если он не равен нулю, а все
остальные миноры порядка
называется
базисным, если он не равен нулю, а все
остальные миноры порядка ![]() равны
нулю или миноров порядка
вообще
нет, то есть
совпадает
с меньшим из чисел
равны
нулю или миноров порядка
вообще
нет, то есть
совпадает
с меньшим из чисел ![]() или
или![]() .
.
Очевидно, что в матрице может быть несколько базисных миноров, но все они должны быть одного порядка.
Определение 6.3.5. Рангом матрицы называется порядок базисного минора.
Обозначается
ранг матрицы – ![]() .
Строки и столбцы, на пересечении которых
стоят элементы базисного минора,
называются базисными.
.
Строки и столбцы, на пересечении которых
стоят элементы базисного минора,
называются базисными.
Теорема 6.3.3. (Теорема о базисном миноре). Базисные строки и столбцы линейно независимы. Любая другая строка или столбец матрицы являются линейной комбинацией базисных строк или столбцов.
Доказательство проведем для строк. Покажем вначале, что базисные строки линейно независимы. Если бы они были линейно зависимы, то одна из этих строк была бы линейной комбинацией остальных. Тогда на основании свойств определителя эту комбинацию можно вычесть из указанной строки и получить на ее месте ноли. Но если вся строка состоит из нолей, то минор равен нулю, что противоречит теореме.
Докажем вторую часть этой теоремы. Рассмотрим любой минор -го порядка, включающий в себя базисный. Расположим базисный минор в левом верхнем углу:
 .
.
По определению данный минор равен нулю. Раскроем его по последнему столбцу:
![]() .
.
Здесь ![]() ,
разделим на него все равенство:
,
разделим на него все равенство:
![]()
![]()
Из полученного выражения следует, что -ая строка является линейной комбинацией базисных строк.
Отсюда можно сделать вывод, что число линейно независимых строк или столбцов равно рангу матрицы. Это свойство используется для практического вычисления .
Определения,
понятия, обозначения.
Будем
рассматривать системы из p линейных
алгебраических уравнений с n неизвестными
переменными (pможет
быть равно n)
вида
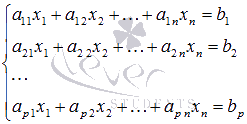
![]() -
неизвестные переменные,
-
неизвестные переменные, ![]() -
коэффициенты (некоторые действительные
или комплексные числа),
-
коэффициенты (некоторые действительные
или комплексные числа), ![]() -
свободные члены (также действительные
или комплексные числа).
Такую
форму записи СЛАУ называют координатной.
В матричной
форме записи
эта система уравнений имеет вид
-
свободные члены (также действительные
или комплексные числа).
Такую
форму записи СЛАУ называют координатной.
В матричной
форме записи
эта система уравнений имеет вид ![]() ,
где
,
где  -
основная матрица системы,
-
основная матрица системы, ![]() -
матрица-столбец неизвестных переменных,
-
матрица-столбец неизвестных переменных, ![]() -
матрица-столбец свободных членов.
Если
к матрице А добавить
в качестве (n+1)-ого столбца
матрицу-столбец свободных членов, то
получим так называемую расширенную
матрицу системы
линейных уравнений. Обычно расширенную
матрицу обозначают буквой Т,
а столбец свободных членов отделяют
вертикальной линией от остальных
столбцов, то есть,
-
матрица-столбец свободных членов.
Если
к матрице А добавить
в качестве (n+1)-ого столбца
матрицу-столбец свободных членов, то
получим так называемую расширенную
матрицу системы
линейных уравнений. Обычно расширенную
матрицу обозначают буквой Т,
а столбец свободных членов отделяют
вертикальной линией от остальных
столбцов, то есть,
 Решением
системы линейных алгебраических
уравнений называют
набор значений неизвестных переменных
Решением
системы линейных алгебраических
уравнений называют
набор значений неизвестных переменных ![]() ,
обращающий все уравнения системы в
тождества. Матричное уравнение
при
данных значениях неизвестных переменных
также обращается в тождество
,
обращающий все уравнения системы в
тождества. Матричное уравнение
при
данных значениях неизвестных переменных
также обращается в тождество ![]() .
Если
система уравнений имеет хотя бы одно
решение, то она называется совместной.
Если
система уравнений решений не имеет, то
она называется несовместной.
Если
СЛАУ имеет единственное решение, то ее
называют определенной;
если решений больше одного, то
–неопределенной.
Если
свободные члены всех уравнений системы
равны нулю
.
Если
система уравнений имеет хотя бы одно
решение, то она называется совместной.
Если
система уравнений решений не имеет, то
она называется несовместной.
Если
СЛАУ имеет единственное решение, то ее
называют определенной;
если решений больше одного, то
–неопределенной.
Если
свободные члены всех уравнений системы
равны нулю ![]() ,
то система называетсяоднородной,
в противном случае – неоднородной.
Решение
элементарных систем линейных
алгебраических уравнений.
Если
число уравнений системы равно числу
неизвестных переменных и определитель
основной ее основной матрицы не равен
нулю, то такие СЛАУ будем
называть элементарными.
Такие системы уравнений имеют единственное
решение, причем в случае однородной
системы все неизвестные переменные
равны нулю.
Такие СЛАУ мы начинали
изучать в средней школе. При их решении
мы брали какое-нибудь одно уравнение,
выражали одну неизвестную переменную
через другие и подставляли ее в оставшиеся
уравнения, следом брали следующее
уравнение, выражали следующую неизвестную
переменную и подставляли в другие
уравнения и так далее. Или пользовались
методом сложения, то есть, складывали
два или более уравнений, чтобы исключить
некоторые неизвестные переменные. Не
будем подробно останавливаться на этих
методах, так как они по сути являются
модификациями метода Гаусса.
Основными
методами решения элементарных систем
линейных уравнений являются метод
Крамера, матричный метод и метод Гаусса.
Разберем их.
Решение
систем линейных уравнений методом
Крамера.
Пусть
нам требуется решить систему линейных
алгебраических уравнений
,
то система называетсяоднородной,
в противном случае – неоднородной.
Решение
элементарных систем линейных
алгебраических уравнений.
Если
число уравнений системы равно числу
неизвестных переменных и определитель
основной ее основной матрицы не равен
нулю, то такие СЛАУ будем
называть элементарными.
Такие системы уравнений имеют единственное
решение, причем в случае однородной
системы все неизвестные переменные
равны нулю.
Такие СЛАУ мы начинали
изучать в средней школе. При их решении
мы брали какое-нибудь одно уравнение,
выражали одну неизвестную переменную
через другие и подставляли ее в оставшиеся
уравнения, следом брали следующее
уравнение, выражали следующую неизвестную
переменную и подставляли в другие
уравнения и так далее. Или пользовались
методом сложения, то есть, складывали
два или более уравнений, чтобы исключить
некоторые неизвестные переменные. Не
будем подробно останавливаться на этих
методах, так как они по сути являются
модификациями метода Гаусса.
Основными
методами решения элементарных систем
линейных уравнений являются метод
Крамера, матричный метод и метод Гаусса.
Разберем их.
Решение
систем линейных уравнений методом
Крамера.
Пусть
нам требуется решить систему линейных
алгебраических уравнений
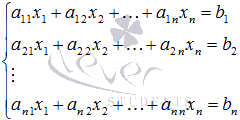 в
которой число уравнений равно числу
неизвестных переменных и определитель
основной матрицы системы отличен от
нуля, то есть,
в
которой число уравнений равно числу
неизвестных переменных и определитель
основной матрицы системы отличен от
нуля, то есть, ![]() .
.
Пусть ![]() -
определитель основной матрицы системы,
а
-
определитель основной матрицы системы,
а ![]() -
определители матриц, которые получаются
из А заменой 1-ого,
2-ого, …, n-ого столбца
соответственно на столбец свободных
членов:
-
определители матриц, которые получаются
из А заменой 1-ого,
2-ого, …, n-ого столбца
соответственно на столбец свободных
членов:
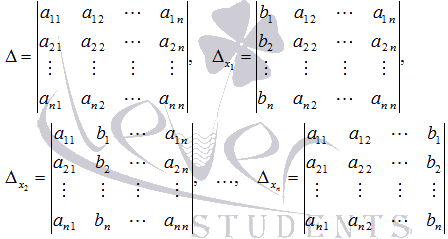 При таких обозначениях неизвестные
переменные вычисляются по формулам
метода Крамера как
При таких обозначениях неизвестные
переменные вычисляются по формулам
метода Крамера как ![]() .
Так находится решение системы линейных
алгебраических уравнений методом
Крамера.
Пример.
Решите
систему линейных уравнений методом
Крамера
.
Так находится решение системы линейных
алгебраических уравнений методом
Крамера.
Пример.
Решите
систему линейных уравнений методом
Крамера 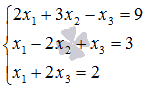 .
Решение.
Основная
матрица системы имеет вид
.
Решение.
Основная
матрица системы имеет вид 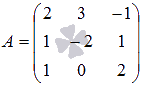 .
Вычислим ее
.
Вычислим ее
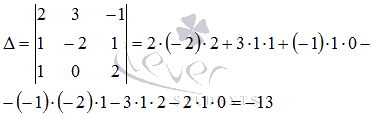 Так
как определитель основной матрицы
системы отличен от нуля, то система
имеет единственное решение, которое
может быть найдено методом Крамера.
Составим
и вычислим необходимые
определители
Так
как определитель основной матрицы
системы отличен от нуля, то система
имеет единственное решение, которое
может быть найдено методом Крамера.
Составим
и вычислим необходимые
определители ![]() (определитель
(определитель ![]() получаем,
заменив в матрице А первый
столбец на столбец свободных членов
получаем,
заменив в матрице А первый
столбец на столбец свободных членов ![]() ,
определитель
,
определитель ![]() -
заменив второй столбец на столбец
свободных членов,
-
заменив второй столбец на столбец
свободных членов, ![]() -
заменив третий столбец матрицы А на
столбец свободных членов):
-
заменив третий столбец матрицы А на
столбец свободных членов):
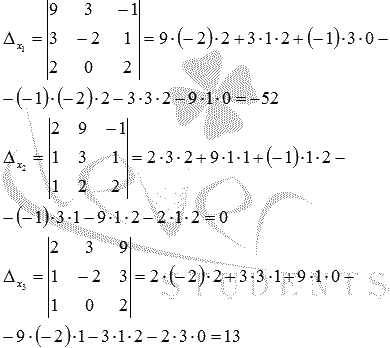 Находим
неизвестные переменные по
формулам
Находим
неизвестные переменные по
формулам ![]() :
:
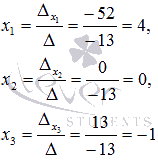 Ответ: x1 =
4, x2 =
0, x3 =
-1.
Основным
недостатком метода Крамера (если это
можно назвать недостатком) является
трудоемкость вычисления определителей,
когда число уравнений системы больше
трех.
Решение
систем линейных алгебраических уравнений
матричным методом (с помощью обратной
матрицы).
Пусть
система линейных алгебраических
уравнений задана в матричной форме
,
где матрица A имеет
размерность n на n и
ее определитель отличен от нуля. Так
как
,
то матрица А –
обратима, то есть, существует обратная
матрица
Ответ: x1 =
4, x2 =
0, x3 =
-1.
Основным
недостатком метода Крамера (если это
можно назвать недостатком) является
трудоемкость вычисления определителей,
когда число уравнений системы больше
трех.
Решение
систем линейных алгебраических уравнений
матричным методом (с помощью обратной
матрицы).
Пусть
система линейных алгебраических
уравнений задана в матричной форме
,
где матрица A имеет
размерность n на n и
ее определитель отличен от нуля. Так
как
,
то матрица А –
обратима, то есть, существует обратная
матрица ![]() .
Если умножить обе части равенства
на
слева,
то получим формулу для нахождения
матрицы-столбца неизвестных переменных
.
Если умножить обе части равенства
на
слева,
то получим формулу для нахождения
матрицы-столбца неизвестных переменных ![]() .
Так мы получили решение системы линейных
алгебраических уравнений матричным
методом.
Пример.
Решите
систему линейных уравнений
матричным
методом.
Решение.
Перепишем
систему уравнений в матричной
форме:
.
Так мы получили решение системы линейных
алгебраических уравнений матричным
методом.
Пример.
Решите
систему линейных уравнений
матричным
методом.
Решение.
Перепишем
систему уравнений в матричной
форме:
![]() Так
как
то
СЛАУ можно решать матричным методом.
С помощью обратной матрицы решение
этой системы может быть найдено
как
Так
как
то
СЛАУ можно решать матричным методом.
С помощью обратной матрицы решение
этой системы может быть найдено
как 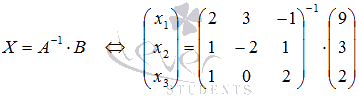 .
Построим
обратную матрицу
с
помощью матрицы из алгебраических
дополнений элементов матрицы А.
.
Построим
обратную матрицу
с
помощью матрицы из алгебраических
дополнений элементов матрицы А.
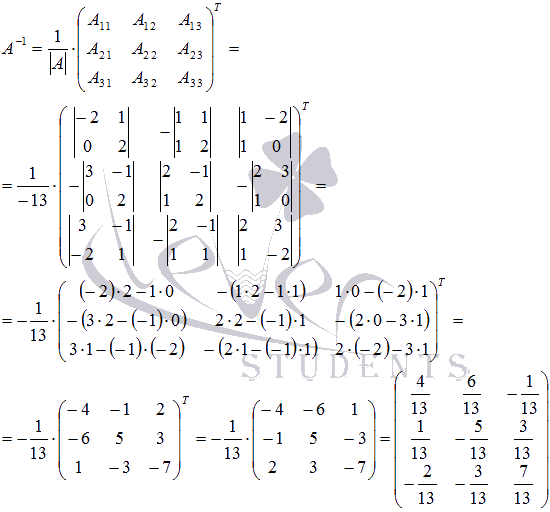 Осталось
вычислить
Осталось
вычислить ![]() -
матрицу неизвестных переменных, умножив
обратную матрицу
-
матрицу неизвестных переменных, умножив
обратную матрицу 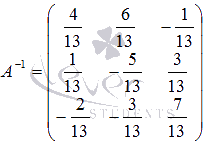 на
матрицу-столбец свободных
членов
на
матрицу-столбец свободных
членов ![]()
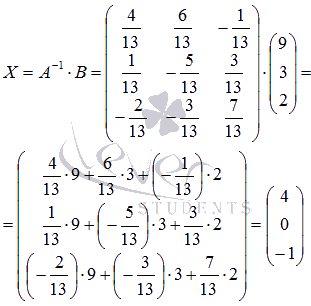 Ответ:
Ответ: ![]() или
в другой записи x1 =
4, x2 =
0, x3 =
-1.
Основная
проблема при нахождении решения систем
линейных алгебраических уравнений
матричным методом заключается в
трудоемкости нахождения обратной
матрицы, особенно для квадратных матриц
порядка выше третьего.
Решение
систем линейных уравнений методом
Гаусса.
Пусть
нам требуется найти решение системы
из n линейных
уравнений с n неизвестными
переменными
или
в другой записи x1 =
4, x2 =
0, x3 =
-1.
Основная
проблема при нахождении решения систем
линейных алгебраических уравнений
матричным методом заключается в
трудоемкости нахождения обратной
матрицы, особенно для квадратных матриц
порядка выше третьего.
Решение
систем линейных уравнений методом
Гаусса.
Пусть
нам требуется найти решение системы
из n линейных
уравнений с n неизвестными
переменными 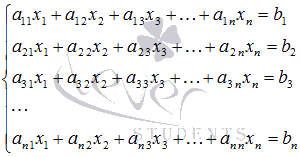 определитель
основной матрицы которой отличен от
нуля.
Суть
метода Гаусса состоит
в последовательном исключении неизвестных
переменных: сначала исключаетсяx1 из
всех уравнений системы, начиная со
второго, далее исключается x2 из
всех уравнений, начиная с третьего, и
так далее, пока в последнем уравнении
останется только неизвестная
переменная xn.
Такой процесс преобразования уравнений
системы для последовательного исключения
неизвестных переменных называется прямым
ходом метода Гаусса.
После завершения прямого хода метода
Гаусса из последнего уравнения
находится xn,
с помощью этого значения из предпоследнего
уравнения вычисляется xn-1,
и так далее, из первого уравнения
находится x1.
Процесс вычисления неизвестных
переменных при движении от последнего
уравнения системы к первому
называется обратным
ходом метода Гаусса.
Кратко
опишем алгоритм исключения неизвестных
переменных.
Будем считать, что
определитель
основной матрицы которой отличен от
нуля.
Суть
метода Гаусса состоит
в последовательном исключении неизвестных
переменных: сначала исключаетсяx1 из
всех уравнений системы, начиная со
второго, далее исключается x2 из
всех уравнений, начиная с третьего, и
так далее, пока в последнем уравнении
останется только неизвестная
переменная xn.
Такой процесс преобразования уравнений
системы для последовательного исключения
неизвестных переменных называется прямым
ходом метода Гаусса.
После завершения прямого хода метода
Гаусса из последнего уравнения
находится xn,
с помощью этого значения из предпоследнего
уравнения вычисляется xn-1,
и так далее, из первого уравнения
находится x1.
Процесс вычисления неизвестных
переменных при движении от последнего
уравнения системы к первому
называется обратным
ходом метода Гаусса.
Кратко
опишем алгоритм исключения неизвестных
переменных.
Будем считать, что ![]() ,
так как мы всегда можем этого добиться
перестановкой местами уравнений
системы. Исключим неизвестную
переменную x1 из
всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное
на
,
так как мы всегда можем этого добиться
перестановкой местами уравнений
системы. Исключим неизвестную
переменную x1 из
всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное
на ![]() ,
к третьему уравнению прибавим первое,
умноженное на
,
к третьему уравнению прибавим первое,
умноженное на ![]() ,
и так далее, к n-ому уравнению
прибавим первое, умноженное на
,
и так далее, к n-ому уравнению
прибавим первое, умноженное на ![]() .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид
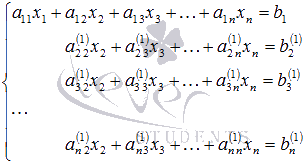 где
где ![]() ,
а
,
а ![]() .
К
такому же результату мы бы пришли, если
бы выразили x1 через
другие неизвестные переменные в первом
уравнении системы и полученное выражение
подставили во все остальные уравнения.
Таким образом, переменная x1 исключена
из всех уравнений, начиная со второго.
Далее
действуем аналогично, но лишь с частью
полученной системы, которая отмечена
на рисунке
.
К
такому же результату мы бы пришли, если
бы выразили x1 через
другие неизвестные переменные в первом
уравнении системы и полученное выражение
подставили во все остальные уравнения.
Таким образом, переменная x1 исключена
из всех уравнений, начиная со второго.
Далее
действуем аналогично, но лишь с частью
полученной системы, которая отмечена
на рисунке
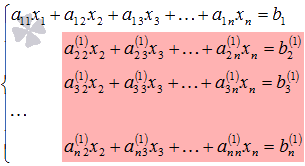 Будем
считать, что
Будем
считать, что ![]() (в
противном случае мы переставим местами
вторую строку с k-ой,
где
(в
противном случае мы переставим местами
вторую строку с k-ой,
где ![]() ).
Приступаем к исключению неизвестной
переменной x2 из
всех уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на
).
Приступаем к исключению неизвестной
переменной x2 из
всех уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на ![]() ,
к четвертому уравнению прибавим второе,
умноженное на
,
к четвертому уравнению прибавим второе,
умноженное на ![]() ,
и так далее, к n-ому уравнению
прибавим второе, умноженное на
,
и так далее, к n-ому уравнению
прибавим второе, умноженное на ![]() .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид
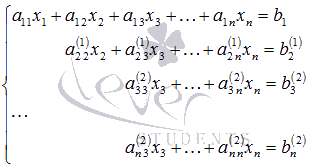 где
где ![]() ,
а
,
а ![]() .
Таким образом, переменная x2 исключена
из всех уравнений, начиная с третьего.
Далее
приступаем к исключению неизвестной x3,
при этом действуем аналогично с
отмеченной на рисунке частью
системы
.
Таким образом, переменная x2 исключена
из всех уравнений, начиная с третьего.
Далее
приступаем к исключению неизвестной x3,
при этом действуем аналогично с
отмеченной на рисунке частью
системы
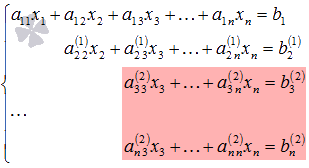 Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
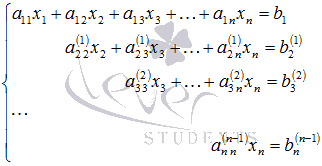 С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xn из
последнего уравнения как
С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xn из
последнего уравнения как ![]() ,
с помощью полученного значения xn находим xn-1из
предпоследнего уравнения, и так далее,
находим x1 из
первого уравнения.
Пример.
Решите
систему линейных уравнений
методом
Гаусса.
Решение.
Исключим
неизвестную переменную x1 из
второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные
на
,
с помощью полученного значения xn находим xn-1из
предпоследнего уравнения, и так далее,
находим x1 из
первого уравнения.
Пример.
Решите
систему линейных уравнений
методом
Гаусса.
Решение.
Исключим
неизвестную переменную x1 из
второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные
на ![]() и
на
и
на ![]() соответственно:
соответственно:
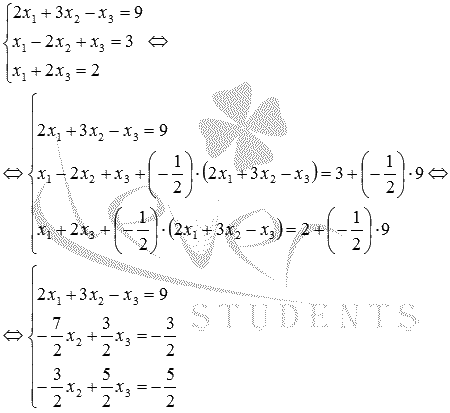
Теперь
из третьего уравнения исключим x2,
прибавив к его левой и правой частям
левую и правую части второго уравнения,
умноженные на ![]() :
:
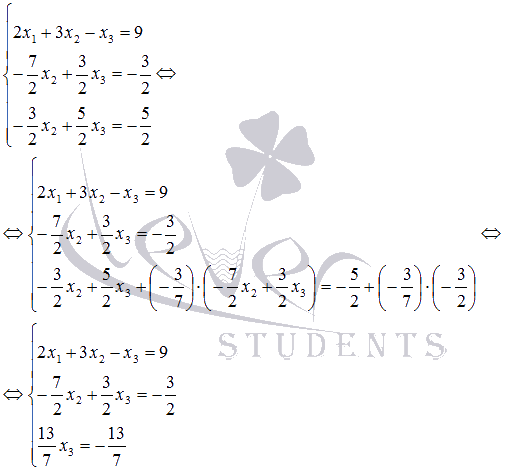 На
этом прямой ход метода Гаусса закончен,
начинаем обратный ход.
Из последнего
уравнения полученной системы уравнений
находим x3:
На
этом прямой ход метода Гаусса закончен,
начинаем обратный ход.
Из последнего
уравнения полученной системы уравнений
находим x3:
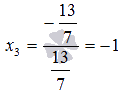 Из
второго уравнения получаем
Из
второго уравнения получаем ![]() .
Из
первого уравнения находим оставшуюся
неизвестную переменную и этим завершаем
обратный ход метода Гаусса
.
Из
первого уравнения находим оставшуюся
неизвестную переменную и этим завершаем
обратный ход метода Гаусса ![]() .
Ответ: x1 =
4, x2 =
0, x3 =
-1.
.
Ответ: x1 =
4, x2 =
0, x3 =
-1.
Решение систем линейных алгебраических уравнений общего вида. В общем случае число уравнений системы p не совпадает с числом неизвестных переменных n: Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная. Прежде чем находить решение системы линейных уравнений необходимо установить ее совместность. Ответ на вопрос когда СЛАУ совместна, а когда несовместна, дает теорема Кронекера – Капелли: для того, чтобы система из p уравнений с n неизвестными (p может быть равно n) была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы, то есть,Rank(A) = Rank(T). Рассмотрим на примере применение теоремы Кронекера – Капелли для определения совместности системы линейных уравнений. Пример.
Выясните,
имеет ли система линейных
уравнений ![]() решения.
Решение.
Найдем
ранг основной матрицы системы
решения.
Решение.
Найдем
ранг основной матрицы системы ![]() .
Воспользуемся методом окаймляющих
миноров. Минор второго порядка
.
Воспользуемся методом окаймляющих
миноров. Минор второго порядка ![]() отличен
от нуля. Переберем окаймляющие его
миноры третьего порядка:
отличен
от нуля. Переберем окаймляющие его
миноры третьего порядка:
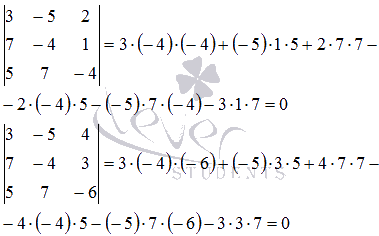 Так
как все окаймляющие миноры третьего
порядка равны нулю, то ранг основной
матрицы равен двум.
В свою очередь
ранг расширенной матрицы
Так
как все окаймляющие миноры третьего
порядка равны нулю, то ранг основной
матрицы равен двум.
В свою очередь
ранг расширенной матрицы ![]() равен
трем, так как минор третьего
порядка
равен
трем, так как минор третьего
порядка
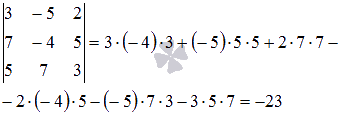 отличен
от нуля.
Таким образом, Rang(A)
< Rang(T),
следовательно, по теореме Кронекера –
Капелли можно сделать вывод, что исходная
система линейных уравнений
несовместна.
Ответ:
система решений не имеет.
Фундаментальной
системой решений однородной
системы из p линейных
алгебраических уравнений с nнеизвестными
переменными называют совокупность (n
– r) линейно
независимых решений этой системы,
где r –
порядок базисного минора основной
матрицы системы.
Если обозначить
линейно независимые решения однородной
СЛАУ как X(1),
X(2),
…, X(n-r) (X(1),
X(2),
…, X(n-r) –
это матрицы столбцы размерности n на 1),то
общее решение этой однородной
системы
отличен
от нуля.
Таким образом, Rang(A)
< Rang(T),
следовательно, по теореме Кронекера –
Капелли можно сделать вывод, что исходная
система линейных уравнений
несовместна.
Ответ:
система решений не имеет.
Фундаментальной
системой решений однородной
системы из p линейных
алгебраических уравнений с nнеизвестными
переменными называют совокупность (n
– r) линейно
независимых решений этой системы,
где r –
порядок базисного минора основной
матрицы системы.
Если обозначить
линейно независимые решения однородной
СЛАУ как X(1),
X(2),
…, X(n-r) (X(1),
X(2),
…, X(n-r) –
это матрицы столбцы размерности n на 1),то
общее решение этой однородной
системы ![]() представляется
в виде линейной комбинации векторов
фундаментальной системы решений с
произвольными постоянными коэффициентами С1,
С2,
…, С(n-r),
то есть,
представляется
в виде линейной комбинации векторов
фундаментальной системы решений с
произвольными постоянными коэффициентами С1,
С2,
…, С(n-r),
то есть, ![]() .
Что
обозначает термин общее решение
однородной системы линейных алгебраических
уравнений (орослау)?
Смысл прост:
формула
задает
все возможные решения исходной СЛАУ,
другими словами, взяв любой набор
значений произвольных постоянных С1,
С2,
…, С(n-r),
по формуле
мы
получим одно из решений исходной
однородной СЛАУ.
Таким образом,
если мы найдем фундаментальную систему
решений, то мы сможем задать все решения
этой однородной СЛАУ как
.
Покажем
процесс построения фундаментальной
системы решений однородной СЛАУ.
Выбираем
базисный минор исходной системы линейных
уравнений, исключаем все остальные
уравнения из системы и переносим в
правые части уравнений системы с
противоположными знаками все слагаемые,
содержащие свободные неизвестные
переменные. Придадим свободным
неизвестным переменным значения1,
0, 0, …, 0 и
вычислим основные неизвестные, решив
полученную элементарную систему
линейных уравнений любым способом,
например, методом Крамера. Так будет
получено X(1) -
первое решение фундаментальной системы.
Если придать свободным неизвестным
значения 0,
1, 0, 0, …, 0 и
вычислить при этом основные неизвестные,
то получим X(2).
И так далее. Если свободным неизвестным
переменным придадим значения0,
0, …, 0, 1 и
вычислим основные неизвестные, то
получим X(n-r).
Так будет построена фундаментальная
система решений однородной СЛАУ и может
быть записано ее общее решение в
виде
.
Для
неоднородных систем линейных
алгебраических уравнений общее решение
представляется в виде
.
Что
обозначает термин общее решение
однородной системы линейных алгебраических
уравнений (орослау)?
Смысл прост:
формула
задает
все возможные решения исходной СЛАУ,
другими словами, взяв любой набор
значений произвольных постоянных С1,
С2,
…, С(n-r),
по формуле
мы
получим одно из решений исходной
однородной СЛАУ.
Таким образом,
если мы найдем фундаментальную систему
решений, то мы сможем задать все решения
этой однородной СЛАУ как
.
Покажем
процесс построения фундаментальной
системы решений однородной СЛАУ.
Выбираем
базисный минор исходной системы линейных
уравнений, исключаем все остальные
уравнения из системы и переносим в
правые части уравнений системы с
противоположными знаками все слагаемые,
содержащие свободные неизвестные
переменные. Придадим свободным
неизвестным переменным значения1,
0, 0, …, 0 и
вычислим основные неизвестные, решив
полученную элементарную систему
линейных уравнений любым способом,
например, методом Крамера. Так будет
получено X(1) -
первое решение фундаментальной системы.
Если придать свободным неизвестным
значения 0,
1, 0, 0, …, 0 и
вычислить при этом основные неизвестные,
то получим X(2).
И так далее. Если свободным неизвестным
переменным придадим значения0,
0, …, 0, 1 и
вычислим основные неизвестные, то
получим X(n-r).
Так будет построена фундаментальная
система решений однородной СЛАУ и может
быть записано ее общее решение в
виде
.
Для
неоднородных систем линейных
алгебраических уравнений общее решение
представляется в виде ![]() ,
где
-
общее решение соответствующей однородной
системы, а
,
где
-
общее решение соответствующей однородной
системы, а ![]() -
частное решение исходной неоднородной
СЛАУ, которое мы получаем, придав
свободным неизвестным значения 0,
0, …, 0 и
вычислив значения основных
неизвестных.
Разберем на
примерах.
Пример.
Найдите
фундаментальную систему решений и
общее решение однородной системы
линейных алгебраических
уравнений
-
частное решение исходной неоднородной
СЛАУ, которое мы получаем, придав
свободным неизвестным значения 0,
0, …, 0 и
вычислив значения основных
неизвестных.
Разберем на
примерах.
Пример.
Найдите
фундаментальную систему решений и
общее решение однородной системы
линейных алгебраических
уравнений  .
Решение.
Ранг
основной матрицы однородных систем
линейных уравнений всегда равен рангу
расширенной матрицы. Найдем ранг
основной матрицы методом окаймляющих
миноров. В качестве ненулевого минора
первого порядка возьмем элемент a1
1 =
9 основной
матрицы системы. Найдем окаймляющий
ненулевой минор второго порядка:
.
Решение.
Ранг
основной матрицы однородных систем
линейных уравнений всегда равен рангу
расширенной матрицы. Найдем ранг
основной матрицы методом окаймляющих
миноров. В качестве ненулевого минора
первого порядка возьмем элемент a1
1 =
9 основной
матрицы системы. Найдем окаймляющий
ненулевой минор второго порядка:
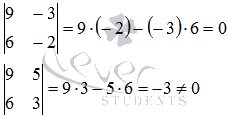 Минор
второго порядка, отличный от нуля,
найден. Переберем окаймляющие его
миноры третьего порядка в поисках
ненулевого:
Минор
второго порядка, отличный от нуля,
найден. Переберем окаймляющие его
миноры третьего порядка в поисках
ненулевого:
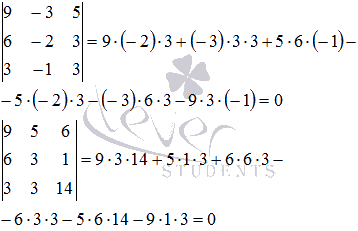
Все
окаймляющие миноры третьего порядка
равны нулю, следовательно, ранг основной
и расширенной матрицы равен двум.
Базисным минором возьмем ![]() .
Отметим для наглядности элементы
системы, которые его образуют:
.
Отметим для наглядности элементы
системы, которые его образуют:
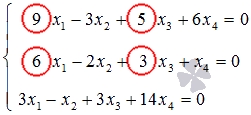 Третье
уравнение исходной СЛАУ не участвует
в образовании базисного минора, поэтому,
может быть исключено:
Третье
уравнение исходной СЛАУ не участвует
в образовании базисного минора, поэтому,
может быть исключено:
![]() Оставляем
в правых частях уравнений слагаемые,
содержащие основные неизвестные, а в
правые части переносим слагаемые со
свободными неизвестными:
Оставляем
в правых частях уравнений слагаемые,
содержащие основные неизвестные, а в
правые части переносим слагаемые со
свободными неизвестными:
![]() Построим
фундаментальную систему решений
исходной однородной системы линейных
уравнений. Фундаментальная система
решений данной СЛАУ состоит из двух
решений, так как исходная СЛАУ содержит
четыре неизвестных переменных, а порядок
ее базисного минора равен двум. Для
нахождения X(1) придадим
свободным неизвестным переменным
значения x2 =
1, x4 =
0,
тогда основные неизвестные найдем из
системы уравнений
Построим
фундаментальную систему решений
исходной однородной системы линейных
уравнений. Фундаментальная система
решений данной СЛАУ состоит из двух
решений, так как исходная СЛАУ содержит
четыре неизвестных переменных, а порядок
ее базисного минора равен двум. Для
нахождения X(1) придадим
свободным неизвестным переменным
значения x2 =
1, x4 =
0,
тогда основные неизвестные найдем из
системы уравнений
![]() .
Решим
ее методом Крамера:
.
Решим
ее методом Крамера:
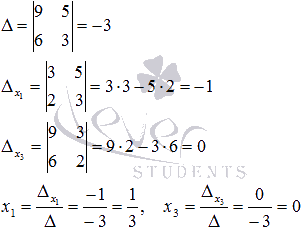 Таким
образом,
Таким
образом, ![]() .
Теперь
построим X(2).
Для этого придадим свободным неизвестным
переменным значения x2 =
0, x4 =
1,
тогда основные неизвестные найдем из
системы линейных уравнений
.
Теперь
построим X(2).
Для этого придадим свободным неизвестным
переменным значения x2 =
0, x4 =
1,
тогда основные неизвестные найдем из
системы линейных уравнений
![]() .
Опять
воспользуемся методом Крамера:
.
Опять
воспользуемся методом Крамера:
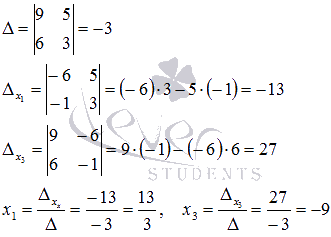 Получаем
Получаем  .
.
Так
мы получили два вектора фундаментальной
системы решений
и ![]() ,
теперь мы можем записать общее решение
однородной системы линейных алгебраических
уравнений:
,
теперь мы можем записать общее решение
однородной системы линейных алгебраических
уравнений:
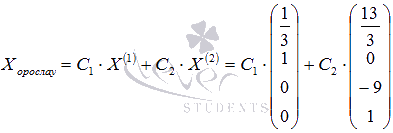 ,
где C1 и C2 –
произвольные числа.
,
где C1 и C2 –
произвольные числа.
Структура общего решения неоднородной линейной системы.
Рассмотрим неоднородную линейную систему (2.2):
 .
.
Докажем следующие свойства ее решений:
Свойство 1. Сумма любого решения системы (2.2) и любого решения соответствующей однородной системы (4.2) является решением системы (2.2).
Доказательство.
Пусть с1, с2,…,сn – решение системы (2.2), а d1, d2,…,dn – решение системы (4.2) с теми же коэффициентами при неизвестных. Подставим в систему (2.2) xi=ci+di:
 .
.
После перегруппировки слагаемых получим:
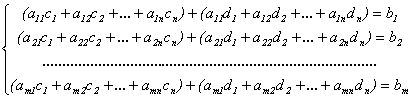 .
.
Но ![]() Следовательно, xi=ci+di является
решением системы (2.2).
Следовательно, xi=ci+di является
решением системы (2.2).
Свойство 2. Разность любых двух решений неоднородной системы (2.2) является решением соответствующей однородной системы (4.2).
Доказательство.
Пусть ![]() и
и ![]() -
решения системы (2.2). Тогда
-
решения системы (2.2). Тогда
![]() Утверждение
доказано.
Утверждение
доказано.
Следствие. Общее решение неоднородной системы (2.2) представляет собой сумму общего решения соответствующей однородной системы (4.2) и частного решения системы (2.2).
Пример.
Общее
решение системы  можно
записать в виде:
можно
записать в виде:
 ,
где
,
где ![]() -
частное решение данной системы.
-
частное решение данной системы.
2.1.1. Пространство арифметических векторов R n. Линейные операции с векторами
Определение. Арифметическим
вектором называется упорядоченная
совокупность n чисел. Обозначается ![]() ,
числа
,
числа ![]() называются
компонентами арифметического вектора.
называются
компонентами арифметического вектора.
Для
арифметических векторов определены
линейные операции — сложение
арифметических векторов и умножение
вектора на число: ![]() ,
,
для
любых ![]() и
и ![]() и
любого числа
и
любого числа ![]()
Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством рифметических векторов Rn.
Вектор ![]() называется
нулевым вектором, а вектор
называется
нулевым вектором, а вектор ![]() —
противоположным вектором для вектора
.
—
противоположным вектором для вектора
.
Для
любых
,
, ![]() из Rn и
любых чисел , справедливо:
из Rn и
любых чисел , справедливо:
 ,
сложение коммутативно;
,
сложение коммутативно; ,сложение
ассоциативно;
,сложение
ассоциативно;
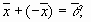
 ,
умножение на число ассоциативно;
,
умножение на число ассоциативно; ;
; ,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение на число дистрибутивно
относительно сложения элементов; ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме.
2.1.2. Линейная зависимость и линейная независимость в Rn
Говорят,
что вектор
пространства Rn линейно
выражается через
векторы ![]() ,
если его можно представить в виде линейной
комбинации этих
элементов
,
если его можно представить в виде линейной
комбинации этих
элементов ![]() ,
т.е. представить в виде
,
т.е. представить в виде ![]() .
.
Определение. Если
хотя бы один вектор системы векторов ![]() из
Rn линейно
выражается через остальные векторы
системы, то система векторов называется
линейно зависимой.
из
Rn линейно
выражается через остальные векторы
системы, то система векторов называется
линейно зависимой.
Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.
2.1.3. Необходимое и достаточное условие линейной зависимости системы векторов
Справедливо следующее утверждение.
Теорема. Система
векторов
из Rn линейно
зависима тогда и только тогда, когда
хотя бы один вектор системы векторов
из
Rn линейно
выражается через остальные векторы
системы.![]()
Это утверждение (необходимое и достаточное условие линейной зависимости) доказано на лекции.
Нетрудно доказать, что система арифметических векторов

линейно
независима и что для любого ![]() из Rn система
векторов
из Rn система
векторов ![]() линейно
зависима:
линейно
зависима: ![]() .
.
2.1.4. Необходимое условие линейной независимости системы векторов (в координатах)
Теорема
(необходимое и достаточное условие
линейной независимости в координатной
форме). Cистема
векторов ![]() из
Rn линейно
независима тогда и только тогда, когда
отличен от нуля определитель, строками
(столбцами) которого являются компоненты
векторов системы:
из
Rn линейно
независима тогда и только тогда, когда
отличен от нуля определитель, строками
(столбцами) которого являются компоненты
векторов системы:

Теорема доказана на лекции.
Следствиями из этой теоремы являются следующие утверждения:
если
 ,
то система векторов
из
Rn —
линейно зависима;
,
то система векторов
из
Rn —
линейно зависима;любая система векторов
 из
Rn, k
> n —
линейно зависима.
из
Rn, k
> n —
линейно зависима.
2.2. Размерность пространства Rn. Базис в Rn
2.2.1. Свойства базиса, естественный базис, координаты вектора в заданном базисе
Итак установлено, что в пространстве Rn существует система из n линейно независимых векторов, а любые n+1 вектора линейно зависимы.
Число n — размерность пространства Rn.
Определение. Любая
упорядоченная линейно независимая
система n векторов ![]() пространства
арифметических векторов Rn называется
базисом в Rn .
пространства
арифметических векторов Rn называется
базисом в Rn .
Нетрудно
показать, что любой вектор ![]() единственным образом
выражается через векторы базиса:
.
(На лекции единственность доказана).
единственным образом
выражается через векторы базиса:
.
(На лекции единственность доказана).
Числа называют координатами вектора в базисе .
Линейно независимая система векторов
образует базис в Rn , который называют естественным базисом в Rn.
Линейные преобразования линейного пространства
Определение линейного оператора
Преобразование
(оператор, отображение) f линейного
пространства в себя (запись ![]() )
называется линейным, если:
)
называется линейным, если:
![]()
Условия 1 и 2 равносильны соотношению
![]()
Матрица
линейного оператора
Матрица
линейного оператора ![]() в
базисе (
в
базисе (![]() )
- матрица
)
- матрица
столбцами
которой являются столбцы образов
базисных векторов ![]() оператора f,
т. е.
оператора f,
т. е. ![]()
Линейный оператор называется невырожденным, если его определитель не равен 0.
Нахождение собственных чисел и собственных векторов матриц
Теорема 19.1 Собственными
числами матрицы ![]() являются
корни уравнения
являются
корни уравнения
![]()
и только они.
Доказательство.
Пусть столбец ![]() --
собственный вектор матрицы
с
собственным числом
--
собственный вектор матрицы
с
собственным числом ![]() .
Тогда, по определению,
.
Тогда, по определению, ![]() .
Это равенство можно переписать в
виде
.
Это равенство можно переписать в
виде ![]() .
Так как для единичной матрицы
.
Так как для единичной матрицы ![]() выполнено
выполнено ![]() ,
то
,
то ![]() .
По свойству матричного умножения
.
По свойству матричного умножения ![]() и
предыдущее равенство принимает вид
и
предыдущее равенство принимает вид
|
(19.4) |
Допустим,
что определитель матрицы ![]() отличен
от нуля,
отличен
от нуля, ![]() .
Тогда у этой матрицы существует
обратная
.
Тогда у этой матрицы существует
обратная ![]() .
Из равенства (19.4)
получим, что
.
Из равенства (19.4)
получим, что ![]() ,
что противоречит определению собственного
вектора. Значит, предположение, что
,
неверно, то есть все собственные числа
должны являться корнями уравнения
.
,
что противоречит определению собственного
вектора. Значит, предположение, что
,
неверно, то есть все собственные числа
должны являться корнями уравнения
.
Пусть
--
корень уравнения
.
Тогда базисный минор матрицы
не
может совпадать с определителем матрицы
и поэтому ![]() ,
, ![]() --
порядок матрицы
.
Уравнение (19.4)
является матричной записью однородной
системы линейных уравнений с
неизвестными
--
порядок матрицы
.
Уравнение (19.4)
является матричной записью однородной
системы линейных уравнений с
неизвестными ![]() ,
являющимися элементами матрицы-столбца
.
По теореме
15.3число
решений в фундаментальной системе
решений равно
,
являющимися элементами матрицы-столбца
.
По теореме
15.3число
решений в фундаментальной системе
решений равно ![]() ,
что больше нуля. Таким образом,
система (19.4)
имеет хотя бы одно ненулевое решение,
то есть числу
соответствует
хотя бы один собственный вектор
матрицы
.
,
что больше нуля. Таким образом,
система (19.4)
имеет хотя бы одно ненулевое решение,
то есть числу
соответствует
хотя бы один собственный вектор
матрицы
.
Определитель ![]() является
многочленом степени
от
переменного
,
так как при вычислении определителя
никаких арифметических действий кроме
сложения, вычитания и умножения выполнять
не приходится.
является
многочленом степени
от
переменного
,
так как при вычислении определителя
никаких арифметических действий кроме
сложения, вычитания и умножения выполнять
не приходится.
Определение 19.5 Матрица называется характеристической матрицей матрицы , многочлен называется характеристическим многочленом матрицы , уравнение называется характеристическим уравнением матрицы .
Пример 19.10 Найдите собственные числа и собственные векторы матрицы
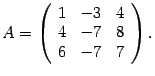
Решение. Составляем характеристическую матрицу :
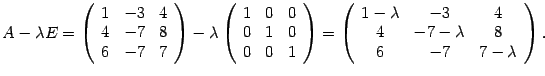
Находим характеристический многочлен
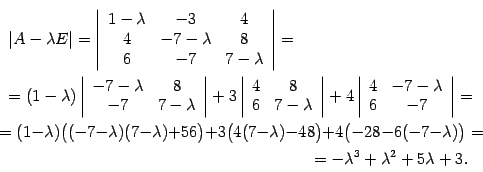 Решим
характеристическое уравнение
Решим
характеристическое уравнение![]()
Подбором
находим, что один корень уравнения
равен -1
.
Есть теорема, которая говорит, что если
число ![]() является
корнем многочлена
является
корнем многочлена ![]() ,
то многочлен
делится
на разность
,
то многочлен
делится
на разность  ,
то есть
,
то есть ![]() ,
где
,
где ![]() --
многочлен. В соответствии с этой теоремой
многочлен
--
многочлен. В соответствии с этой теоремой
многочлен ![]() должен
делиться на
должен
делиться на ![]() .
Выделим в характеристическом многочлене
этот множитель
.
Выделим в характеристическом многочлене
этот множитель ![]() :
:
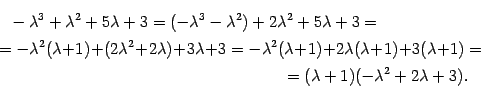 Находим
корни трехчлена
Находим
корни трехчлена ![]() .
Они равны
-1 и
3. Таким образом,
.
Они равны
-1 и
3. Таким образом,
![]()
![]() --
корень кратности 2 17.7 b,
--
корень кратности 2 17.7 b, ![]() --
простой корень. Итак, собственные числа
матрицы
равны
,
.
Найдем соответствующие им собственные
векторы.
--
простой корень. Итак, собственные числа
матрицы
равны
,
.
Найдем соответствующие им собственные
векторы.
Пусть ![]() ,
тогда для собственного вектора
получаем
матричное уравнение
,
тогда для собственного вектора
получаем
матричное уравнение
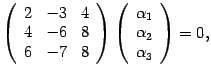 что
соответствует системе уравнений
что
соответствует системе уравнений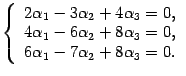
Решаем
ее методом Гаусса Выписываем расширенную
матрицу системы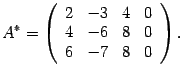
Первую строку, умноженную на числа -2 и -3 прибавляем соответственно ко второй и третьей строкам
![]() Меняем
местами вторую и третью строки
Меняем
местами вторую и третью строки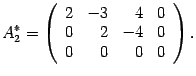 Возвращаемся
к системе уравнений
Возвращаемся
к системе уравнений
![]()
Базисный
минор матрицы ![]() находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальня
система содержит только одно решение.
Переменные
находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальня
система содержит только одно решение.
Переменные ![]() и
и ![]() оставляем
в левой части, а переменное
оставляем
в левой части, а переменное ![]() переносим
в правую часть
переносим
в правую часть
![]()
Полагаем ![]() ,
находим
,
находим ![]() ,
, ![]() .
Итак, собственному числу
соответствует
собственный вектор
.
Итак, собственному числу
соответствует
собственный вектор 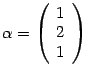 .
.
Пусть ![]() ,
тогда для собственного вектора
,
тогда для собственного вектора ![]() получаем
матричное уравнение
получаем
матричное уравнение
![]() что
соответствует системе уравнений
что
соответствует системе уравнений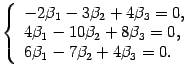
Решаем ее методом Гаусса. Выписываем расширенную матрицу
![]()
Первую строку умножаем на числа 2 и 3 и прибавляем соответственно ко второй и третьей строкам
![]() Вторую
строку умножаем на
-1 и
прибавляем к третьей
Вторую
строку умножаем на
-1 и
прибавляем к третьей
![]() Возвращаемся
к системе уравнений
Возвращаемся
к системе уравнений![]()
Базисный
минор матрицы
находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому
фундаментальная система содержит
только одно решение. Переменные ![]() и
и ![]() оставляем
в левой части, а переменное
оставляем
в левой части, а переменное ![]() переносим
в правую часть
переносим
в правую часть
![]()
Полагаем ![]() ,
находим
,
находим ![]() ,
, ![]() .
Итак, собственному числу
соответствует
собственный вектор
.
Итак, собственному числу
соответствует
собственный вектор ![]() .
Чтобы избавиться от дроби, умножим
собственный вектор на 2, получим
собственный вектор с тем же самым
собственным числом. В итоге собственному
числу
соответствует
собственный вектор
.
Чтобы избавиться от дроби, умножим
собственный вектор на 2, получим
собственный вектор с тем же самым
собственным числом. В итоге собственному
числу
соответствует
собственный вектор  .
.
Ответ: Собственные числа: , , соответствующие собственные векторы: , .
