1.2. Внутренняя энергия, теплота и работа. Первый закон термодинамики

Неотъемлемым свойством материи является движение. Мерой движения является энергия. Важным термодинамическим свойством системы является ее внутренняя энергия.

Внутренняя энергия  это общий запас энергии системы за вычетом кинетической энергии системы в целом и ее потенциальной энергии положения. С позиций молекулярно-кинетической теории физический смысл внутренней энергии определяется следующим образом. Это совокупность всех видов энергии частиц в системе, т.е. сумма энергий поступательного, колебательного, вращательного движения молекул, энергия взаимодействия между молекулами, энергия связей атомов в молекуле, энергия электронов, ядер атомов и т.д. Внутренняя энергия системы зависит от природы вещества, его массы и от параметров состояния системы. Абсолютная величина внутренней энергии любой системы неизвестна, но в химической термодинамике достаточно знать только изменение внутренней энергии в ходе процесса. Размерность внутренней энергии (“U”) Дж или Дж/моль.

Внутреннюю энергию системы можно увеличить двумя путями:

- совершив какую-либо работу над системой;

0. - сообщив системе какое-то количество теплоты.

(Чтобы уменьшить внутреннюю энергию, работа должна быть совершена системой, а теплота  из системы выделиться).

Таким образом, теплота и работа характеризуют качественно и количественно две формы передачи энергии от одного тела к другому. В первом случае передача энергии происходит за счет перемещения масс, состоящих из большого числа частиц под действием каких-либо сил (работа). Во втором случае передача энергии происходит за счет хаотического столкновения молекул двух соприкасающихся тел (теплота). Во многих процессах изменение внутренней энергии осуществляется частично за счет передачи тепла и частично за счет совершения работы. Теплота (Q) и работа (А) имеют ту же размерность, что и внутренняя энергия. Бесконечно малые количества теплоты и работы обозначают: Q и А.

Теплота, полученная системой, считается положительной (Q > 0), это эндотермический процесс, отданная системой  отрицательна (Q < 0), это экзотермический процесс. Работа, совершаемая системой против внешних сил, считается положительной (А > 0); работа, совершаемая над системой  отрицательна (А < 0).

Работа всегда может быть выражена как произведение обобщенной силы на изменение обобщенной координаты:

(1.3)

Например, работа расширения идеального газа:

(1.4)

Сила  есть фактор интенсивности.

Координата  фактор экстенсивности (или емкости).

Аналогично этому теплота тоже может быть выражена как произведение постоянной величины фактора интенсивности (Т) на изменение фактора емкости (энтропия S):

(1.5)

.

Взаимосвязь между внутренней энергией, теплотой и работой устанавливается на основе первого закона (начала) термодинамики. Он является постулатом, вытекающим из опыта, и представляет собой одну из форм закона сохранения энергии, установленного в современном виде Гессом (1840), Майером (1842), Джоулем (1842) и Гельмгольцем (1847).

Существует ряд формулировок первого закона термодинамики, которые равноценны и вытекают одна из другой. Приведем некоторые из них.

0. “В любой изолированной системе общий запас энергии остается постоянным”.

1. “Разные формы энергии переходят друг в друга в строго эквивалентных количествах”.

2. “Вечный двигатель первого рода невозможен, т.е. невозможно построить машину, которая производила бы механическую работу, не затрачивая на это эквивалентного количества внутренней энергии”.

Математическая формулировка первого закона термодинамики:

δQ=dU+δA, (1.6)

т.е. теплота, сообщенная системе, расходуется на приращение внутренней энергии и на совершение системой работы.

В интегральной форме:

(1.7)

“А”  это сумма всех видов работ, совершаемых системой. Она может быть представлена как сумма двух слагаемых: полезная работа А^´_., т.е. работа за счет химических, электрических и других подобных сил и работа расширения.

Для многих систем работа расширения является единственным видом работ.

Работа расширения идеального газа:

(1.8)

или в интегральной форме:

(1.9)

В изобарном процессе (Р = const):

(1.10)

С учетом этого для процессов, единственным видом работы в которых является работа расширения, I закон термодинамики запишется таким образом:

(1.11)

или

(1.12)

Бесконечно малые количества теплоты и работы мы обозначаем значком   частный дифференциал, а для внутренней энергии применяем значок d  полного дифференциала.

Эта запись имеет большой физический смысл. Рассмотрим два состояния изолированной системы: состояние 1 и состояние 2. В каждом из них система имеет определенные значения параметров P, T, V и т.д. Меняя эти параметры, переведем систему из состояния 1 в состояние 2 по пути l₁, а затем вернем ее из состояния 2 в состояние 1 другим путем  l₂ (рис. 1.1).

Такой процесс, как мы уже знаем, называется циклом, или круговым процессом.

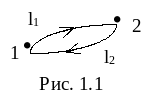
Изменение внутренней энергии в круговом процессе равно нулю. Это следует из закона сохранения энергии. В противном случае можно было бы, вернувшись в исходное состояние, получить выигрыш энергии из ничего или бесследно ее потерять. Отсюда следует, что внутренняя энергия является функцией состояния системы, т.е. ее изменение не зависит от пути процесcа, а зависит только от начального и конечного состояния системы, и интеграл по замкнутому контуру

(1.13)

Из математики нам известно, что если интеграл по замкнутому контуру от некоторого подинтегрального выражения равен нулю, то это подинтегральное выражение является полным дифференциалом некоторой функции. Поэтому бесконечно малое приращение внутренней энергии есть полный дифференциал: dU.

Теплота и работа (по отдельности) в круговом процессе не равны нулю, они не являются функциями состояния системы, т.е. зависят от пути процесса. Их бесконечно малые приращения не являются полными дифференциалами и обозначаются Q и A. Таким образом, теплота и работа являются характеристиками процесса, а внутренняя энергия  есть принадлежность, характеристика состояния системы.