5.9. Закон распределения Нернста. Экстракция

Рассмотрим систему, состоящую из двух практически не растворимых друг в друге жидкостей. Если к такой системе добавить третью жидкость, которая растворима и в первом, и во втором растворителях, то распределение третьего компонента между двумя несмешивающимися жидкостями будет происходить в соответствии с законом распределения Нернста: «В равновесной гетерогенной системе, состоящей из двух нерастворимых или ограниченно растворимых жидкостей, отношение концентраций третьего компонента, распределяющегося между ними, есть величина постоянная, зависящая только от температуры»:

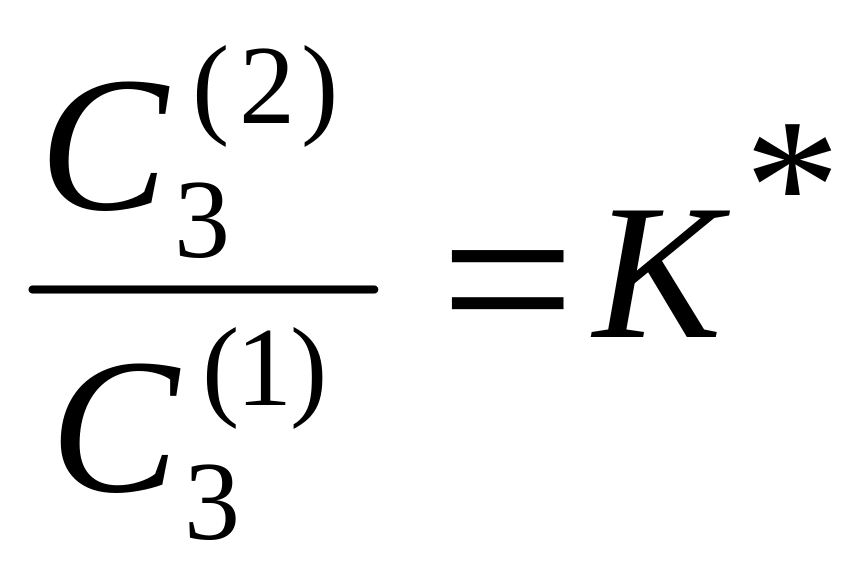(5.52)

К^* – коэффициент распределения, зависящий от природы веществ и от температуры. Закон распределения Нернста выполняется в виде уравнения (5.52) при условии отсутствия диссоциации и ассоциации молекул распределяющегося компонента и отсутствии его влияния на взаимную растворимость 1-го и 2-го растворителей. Например, при распределении янтарной кислоты С₂Н₄(СООН)₂ между этиловым спиртом (2) и водой (1), она практически не диссоциирует в них и К*=5,38 при 298 К.

В общем случае:

(5.53)

При ассоциации молекул растворенного вещества n и m меньше единицы, при диссоциации – больше единицы. Так, например, при распределении салициловой кислоты, С₆Н₄(ОН)СООН, между водой (1) и бензолом (2) при 298 К , происходит её частичная диссоциация в воде, и закон распределения для этой системы выразится уравнением: .

Закон распределения можно обосновать теоретически, учитывая, что равновесие растворенного вещества в двух несмешивающихся растворителях характеризуется равенством его химических потенциалов в обеих фазах:

, (5.54)

откуда:

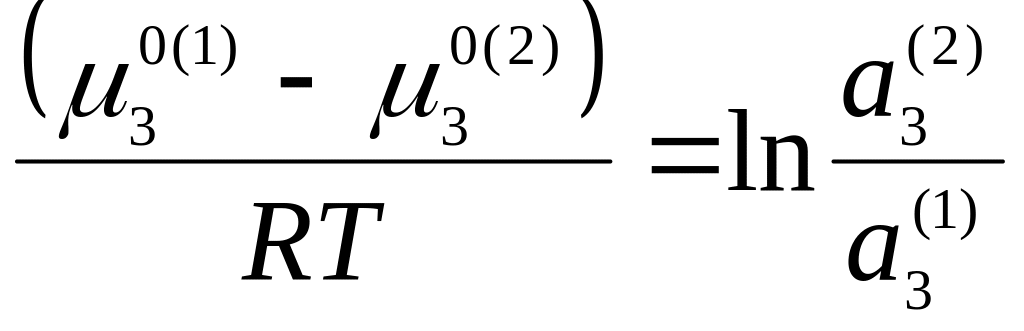(5.55)

Так как стандартные химические потенциалы веществ, , а также R и T – постоянны, то и отношение активностей компонента 3 в первом и втором растворителях постоянно, т.е.

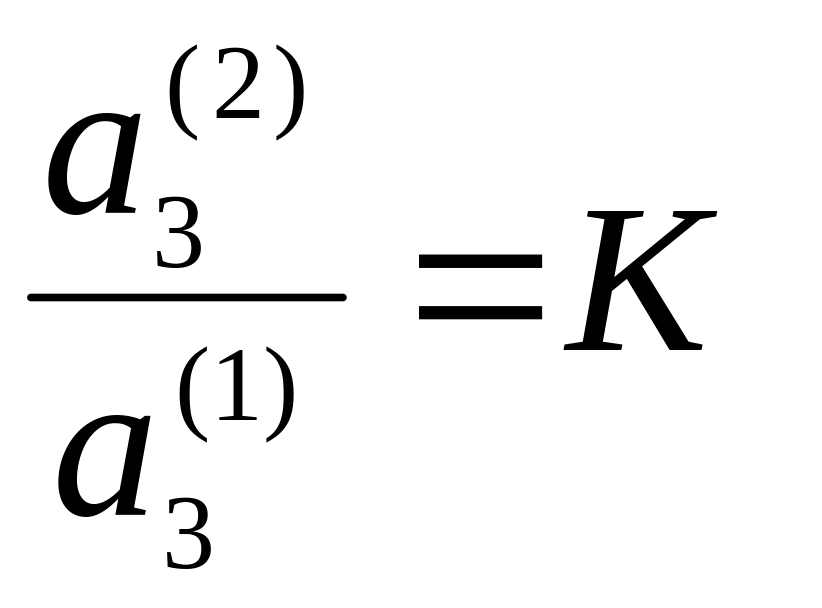(5.56)

Выразим активности через коэффициенты активностей f и концентрации C:

(5.57)

очевидно, что соотношение констант К и К^* выражается уравнением:

(5.58)

Строго говоря, формальный коэффициент распределения К* зависит от концентрации растворенного вещества в обоих растворителях, поскольку коэффициент активности f зависит от концентрации веществ. С разбавлением, когда f →1, К перестает зависеть от концентрации и становится равен К.

На законе распределения Нернста основан метод извлечения растворенного вещества из раствора при помощи второго растворителя.

Этот метод называется экстракцией. Рассмотрим некоторые закономерности процесса экстракции.

Представим себе раствор, состоящий из двух жидкостей: растворителя и растворенного вещества, общим объёмом V₁ (объём экстрагируемого раствора). Допустим, необходимо извлечь растворённое вещество. Добавим к нему некоторый объём другого растворителя (экстрагента) V₂, не смешиваемого с первым. Часть растворенного вещества перейдет во второй растворитель, т. е произойдет экстракция. При необходимости извлечения растворенного вещества, подбирают экстрагент, в котором данное вещество растворимо намного лучше, чем в исходном растворителе. По закону распределения, отношение равновесных концентраций растворенного вещества во втором и первом растворителях: К=С₂/С₁. Допустим, в первом растворителе после экстракции осталось количество растворенного вещества g₁, а во второй растворитель перешло количество вещества g_o – g₁. Тогда:

, (5.59)

где g_o – количество растворённого вещества в первом растворителе до экстракции. Количество вещества, оставшееся в первом растворителе после экстракции, найдем из уравнения 5.59:

(5.60)

Для более полного извлечения вещества повторим экстракцию с новой порцией второго растворителя, добавив его к объёму раствора, оставшегося после первой экстракции. После повторной экстракции в исходном растворителе останется неизвлеченного вещества:

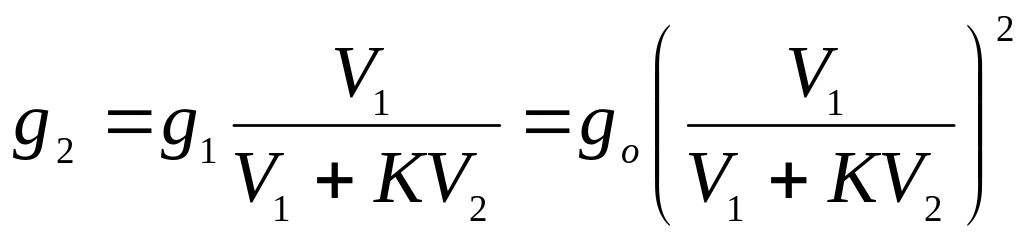(5.61)

После «n» экстракций количество оставшегося в первом растворителе вещества будет

(5.62)

Если экстракцию провести однократно, использовав сразу весь объём растворителя, nV₂ , то количество оставшегося, неэкстрагированного вещества в первом растворителе будет

(5.63)

Сравнение уравнений (5.62) и (5.63) показывает, что, поскольку степенная функция (5.63) убывает быстрее, чем линейная (5.64), очевидно, что количество оставшегося неизвлеченного вещества в первом растворителе будет гораздо больше при однократном использовании растворителя, g^/ . Следовательно, более полное извлечение растворенного вещества достигается при многократной экстракции малыми порциями экстрагента.