5.7. Осмотическое давление

Осмосом называют самопроизвольное проникновение растворителя через полупроницаемую перегородку в раствор. Полупроницаемой перегородку называют потому, что через неё могут проходить только молекулы растворителя, а растворенного вещества – не могут. Сила, заставляющая молекулы растворителя переходить через полупроницаемую перегородку (мембрану), названа осмотическим давлением. Его можно иначе определить как давление, которое необходимо приложить, чтобы прекратить переход растворителя через мембрану. Впервые осмотическое давление было обнаружено Нолле, в 1748 году.

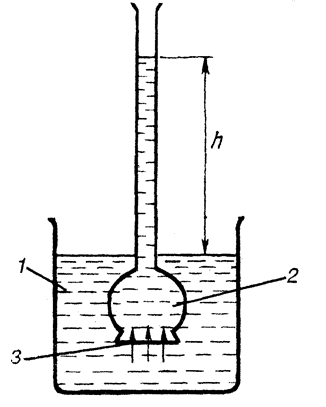
Простейший осмометр изображен на рис. 5.9. Сосуд 2 с водным раствором снизу закрыт мембраной и помещен в сосуд 1, наполненный водой. Вода вследствие осмоса проникает в сосуд 2. Гидростатическое давление столба жидкости в сосуде 2 уравновесит осмотическое давление и установится равновесие.

В 1887 году Вант-Гофф показал, что осмотическое давление π в разбавленных растворах выражается уравнением:

π = СRT (5.43)

Для идеальных растворов уравнение Вант-Гоффа можно получить, исходя из условия равенства химических потенциалов растворителя в растворе μ₁ и в чистом растворителе μ⁰_{1 .}

Это равенство – есть условие установившегося равновесия в системе:

μ₁(N₁, π) = μ⁰₁ (5.44)

Возьмем полный дифференциал от обеих частей уравнения (5.44), учитывая, что химический потенциал чистого растворителя – постоянная величина.

Рис. 5.9. Осмометр

(5.45)

Применяя полученные ранее уравнения для характеристических функций (2.61), с учетом тождества (2.68), можно записать:

, (5.46)

где - парциальный молярный объём растворителя.

Подставляя (5.46) в (5.45), получим уравнение, устанавливающее зависимость осмотического давления от состава раствора и химического потенциала растворителя:

(5.47)

В идеальном растворе изменения объёма компонента при образовании раствора не происходит, поэтому парциальный молярный объём растворителя равен молярному объёму чистого растворителя , а выражается уравнением (2.75). С учетом этого из (5.47) получим:

(5.48)

В результате интегрирования уравнения (5.48) в пределах от 0 до и от 1 до N₁, получим уравнение, выражающее зависимость осмотического давления идеального раствора от состава:

(5.49)

Для предельно разбавленных растворов уравнение (5.49) тоже применимо. Учитывая, что

–lnN₁ = - ln(1-N₂) ≈ N₂ , (5.50)

а молярный объём чистого растворителя равен молярному объёму раствора V, из (5.49) получим:

или , (5.51)

где С – концентрация раствора.

Осмотическое давление играет очень важную роль в процессах жизнедеятельности различных организмов. По закону осмоса происходит распределение различных веществ и воды в тканях человека и животных. Известно, что осмотическое давление крови человека составляет около 8 атм (8,1·10⁵ Па). Недостаток воды в организме проявляется чувством жажды, а утоление её восстанавливает необходимое осмотическое давление крови и восстанавливает водно-солевой баланс. Осмотическое давление служит движущей силой для поглощения влаги прорастающими в почве семенами, благодаря чему, даже при невысокой окружающей влажности, «сосущая сила клетки» может достигать нескольких сотен атмосфер. На применении уравнения Вант-Гоффа основан один из методов определения молярной массы растворенного вещества в разбавленном растворе.