5.4. Диаграммы «давление - состав», «температура – состав» и законы Коновалова для реальных систем
Диаграммы «давление – состав» для реальных растворов без экстремума и с экстремумом изображены в верхнем ряду рис. 5.6. Первый закон Коновалова выполняется и для реальных растворов.
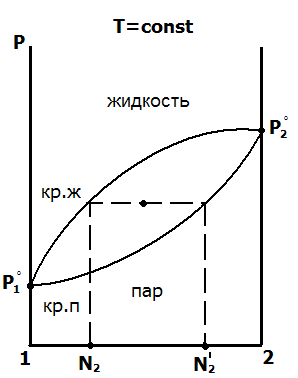
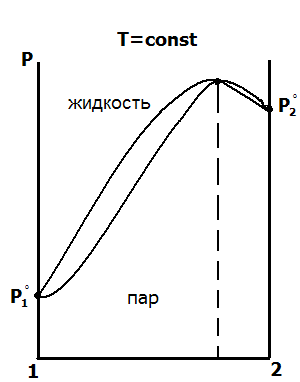
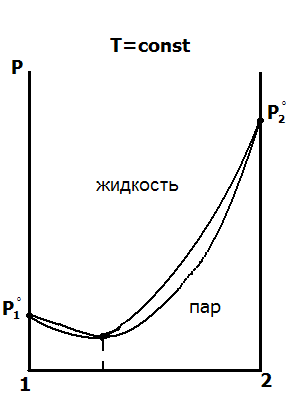
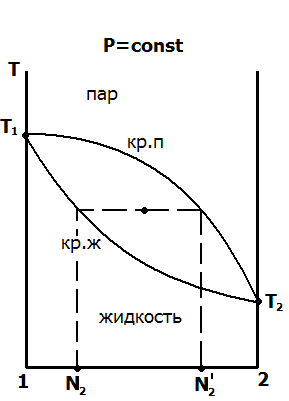
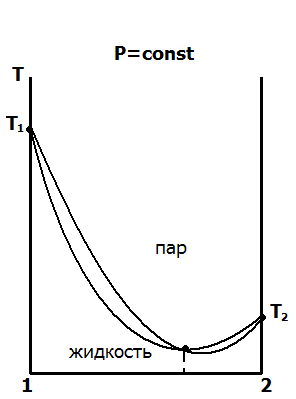
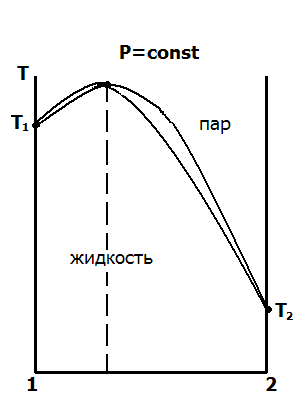
рис. 5.6. Диаграммы «давление – состав» и «температура – состав» для реальных (неидеальных) бинарных летучих жидкостей
Как видно из рисунков с экстремумами, в точках экстремума кривые жидкости и пара соприкасаются, то есть состав жидкости и пара в точках экстремума одинаков. Этот вывод называется вторым законом Коновалова. В термодинамической теории растворов оба закона Коновалова теоретически обоснованы. Их обоснование приводится в параграфе 5.5. Смеси, соответствующие по составу точкам экстремума, называются азеотропными, или нераздельно кипящими. Они ведут себя при нагревании как один компонент, их нельзя разделить простой перегонкой.
Равновесие «жидкость – пар» часто удобнее рассматривать при условии постоянства давления. В этом случае диаграммы «температура – состав» характеризуют температуру кипения жидкостей в зависимости от состава (кривая жидкости) и равновесный состав насыщенного пара при температуре кипения жидкости (кривая пара). Диаграммы «температура – состав» приведены в нижнем ряду на рис. 5.6. При этом следует обратить внимание, что кривые жидкости и область жидкой фазы находятся в этом случае в нижней части диаграммы, а область пара и кривая пара – в верхней части.
Компонент, который более летуч, в данном случае компонент 2, имеет более высокое давление насыщенного пара Рº2 , чем первый, и более низкую температуру кипения.
5.5. Закономерности общего давления пара над смесью двух летучих жидкостей. Обоснование законов Коновалова
В предыдущих параграфах главы мы рассматривали жидкости, имеющие достаточно высокое давление собственного пара. Их называют летучими жидкостями. К смесям летучих жидкостей относятся, например, нефть и продукты её первичной переработки: бензин, керосин.
Рассмотрим двухкомпонентную жидкую
летучую смесь с давлением паров над
чистыми веществами
и
.
Допустим, что оба компонента неограниченно
растворимы друг в друге и смесь паров
над идеальным раствором подчиняется
законам идеальных газов. Допустим также,
что
>
.
Такая система, как мы уже знаем, подчиняется
уравнению Дюгема – Маргулеса (5.13):
dlnP1
= -
dlnP2
По закону Дальтона,
(5.29)
Молярные доли со штрихом относятся к фазе пара.
Из (5.13):
, (5.30)
откуда
(5.31)
Заменим
по уравнению (5.29)
(5.32)
Разделим левую и правую части (5.32) на dN2 :
(5.33)
Общее давление пара над смесью двух летучих жидкостей равно сумме парциальных давлений:
Р = Р1 + Р2 (5.34)
Возьмём производную по N2 от обеих частей уравнения (5.34):
(5.35)
Подставим в (5.35) значение dP1/dN2 из (5/33):
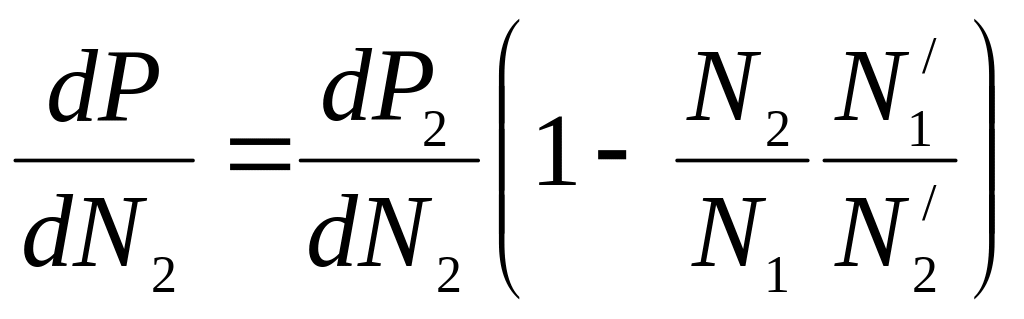(5.36)
где
называется коэффициентом разделения.
Он зависит от состава смеси. Чем больше
отличается состав смеси от состава
равновесного с ней пара, тем больше α
отличается от единицы и тем легче
разделить летучую смесь на компоненты
методом перегонки.
Уравнение (5.36) является основным уравнением для неограниченно смешивающихся жидких бинарных летучих смесей. Проанализируем это уравнение. С ростом содержания компонента в растворе его парциальное давление всегда увеличивается, т.е. dP2/dN2 >0 и dP1/dN1 >0 , а общее давление пара над раствором с изменением состава раствора может как увеличиваться, так и уменьшаться.
Если общее давление пара над раствором увеличивается с ростом содержания второго компонента в растворе, т. е. dP/dN2 >0 то из уравнения (5.36):
>
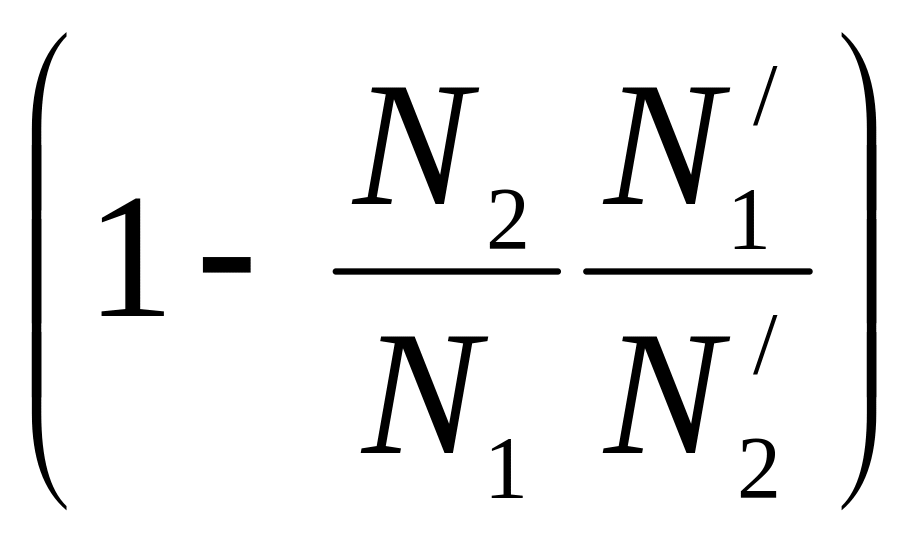0 и
(5.37)
и поэтому
, а
(5.38)
И наоборот, если общее давление пара над раствором уменьшается с ростом молярной доли второго компонента N2, то
, а
(5.39)
Неравенства (5.38) и (5.39) выражают первый закон Коновалова, сформулированный нами ранее на основе анализа диаграмм, в параграфе 5.3.: «Пар над смесью двух летучих жидкостей относительно богаче тем компонентом, добавление которого к жидкости повышает общее давление над раствором при постоянной температуре или понижает температуру кипения раствора при постоянном давлении».
Если на кривой Р=f(N2) имеется экстремум, то в точке экстремума
dP/dN2=0 (5.40)
Тогда, из (5.36) получим:
=0
и
(5.41)
Отсюда получим, что в точке экстремума
(5.42)
Соотношения (5.42) являются теоретическим обоснованием второго закона Коновалова, сформулированного на основе анализа диаграмм в параграфе 5.4.: «Точки экстремума на кривых общее давление пара – состав раствора или на кривых температура кипения – состав раствора отвечают растворам, состав которых одинаков с составом равновесного с ним пара».