5.3. Давление насыщенного пара компонента над раствором. Законы Рауля и Генри. Растворимость газов в жидкостях

Условие равновесия i –компонента в растворе и паре выражается равенством химических потенциалов компонента в растворе μ_i и в паре μ_i'

μ_i = μ_i'

Если пар подчиняется законам идеальных газов, то

μ_i' = μ_iº + RTlnP_i и

dμ_i = RTdlnP_i ,

отсюда

dlnP_i = (5.15)

если 1 – растворитель, а 2 – растворенное вещество, то

dlnP₁ = ; dlnP₂ = (5.16)

где Р₁ – парциальное давление пара растворителя над раствором;

Р₂ – парциальное давление пара растворенного вещества над раствором;

Р₁ + Р₂ = Р – общее давление пара над раствором.

Поскольку существуют отличия в поведении идеальных, предельно разбавленных и реальных растворов, будем рассматривать далее закономерности в поведении каждой из этих групп в отдельности.

А) Идеальные растворы

Химический потенциал каждого из двух компонентов идеального раствора (1 – растворитель, 2 – растворенное вещество) выражается уравнением:

μ_i = μ_iº + RT lnN_i

и

dμ_i = RTdlnN_i (5.17)

подставим (5.17) в (5.15):

dlnP_i = dlnN_i (5.18)

Проинтегрируем (5.18) от Р_iº до Р_i и от N_i = 1 до N_i :

(5.19)

Отсюда Р_i = P_iºN_i (5.20)

Уравнение (5.20) называют уравнением Рауля. В идеальном растворе оно применимо и к растворителю, и к растворенному веществу. В соответствии с уравнением (5.20), равновесное парциальное давление пара компонента над раствором равно произведению давления пара над чистым компонентом Р_iº на его молярную долю в растворе.

Уравнение (5.20) справедливо при постоянной температуре.

Общее давление пара над раствором равно сумме парциальных давлений:

Р = P₁ºN₁ + P₂ºN₂ = Р₁º(1-N₂) + P₂ºN₂

или

Р= P₁º - N₂(P₁º - P₂º) (5.21)

Уравнения (5.20) и (5.21) являются уравнениями прямых в координатах Р₁ – N₁ , P₂ – N₂ , P – N₂ , где N_i – состав раствора.

Представим эти зависимости графически, рис.5.1.

Здесь общее давление пара выражено как функция состава раствора. Если выразить общее давление пара над раствором как функцию состава пара, то получим гиперболическую кривую пара, P=f(N₂^' ), лежащую ниже, чем кривая жидкости, P=f(N₂), рис. 5.2.

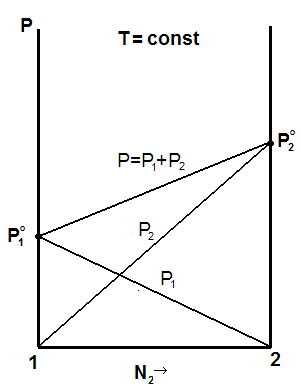
Рис. 5.1. Зависимости общего и парциальных давлений от состава идеального раствора

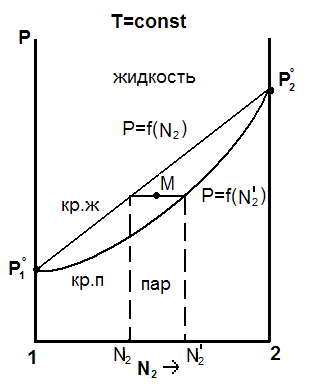
Рис. 5.2. Диаграмма «состав – давление пара» для жидкой бинарной летучей смеси, подчиняющейся законам идеальных растворов

Такая диаграмма называется диаграммой «состав -давление пара». Над кривой жидкости – область жидкости. Под кривой пара – область ненасыщенного пара. Между кривыми – область гетерогенного равновесия жидкость↔пар. Возьмем точку М в гетерогенной области и проведем линию, параллельную оси абсцисс, до пересечения с кривыми жидкости и пара (она называется нода). Полученные точки на кривых характеризуют составы сопряженных фаз: жидкости и насыщенного пара при данной температуре. Как видно из графика, пар относительно богаче равновесной с ним жидкости более летучим компонентом, в данном случае – вторым. Это различие в составах жидкости и пара устанавливается первым законом Коновалова: «Пар над смесью двух летучих жидкостей относительно богаче тем компонентом, добавление которого к жидкости повышает общее давление над раствором при постоянной температуре или понижает температуру кипения раствора при постоянном давлении».

Как будет показано далее, первый закон Коновалова выполняется и в реальных, неидеальных растворах. Это различие в составах жидкости и пара используется для разделения летучих смесей перегонкой (см. раздел 5.5).

Б) Предельно разбавленные растворы

В предельно разбавленном растворе закон Рауля применим только к растворителю:

Р₁ = Р₁ºN₁,

что легко преобразуется к виду:

Р₁º - Р₁ = Р₁º - Р₁ºN₁, или 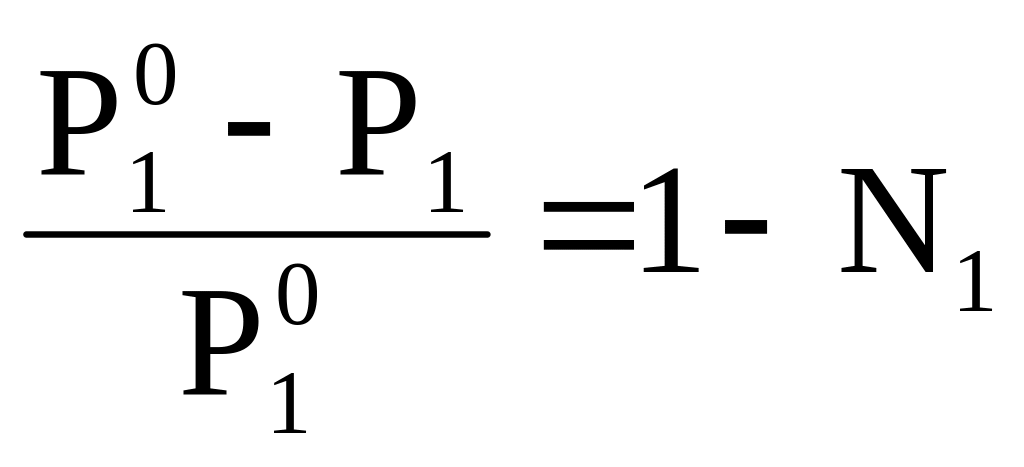, где Р₁º-Р₁ =ΔР₁ – понижение давления пара растворителя над раствором. Тогда

, (5.22)

т.е. относительное понижение давления пара растворителя над раствором пропорционально молярной доле растворенного вещества. Это утверждение, а также его математическая запись (5.22) называется первым законом Рауля.

К растворенному веществу в предельно разбавленных растворах закон Рауля не применим, а применим закон Генри:

Р₂ = К_гN₂ , (5.23)

т.е. парциальное давление пара растворенного вещества над предельно разбавленным раствором пропорционально молярной доле растворенного вещества. Величина К_г называется константой Генри (или коэффициентом Генри). Но К_г ≠ Р₂º, а определяется экстраполяцией опытных данных:

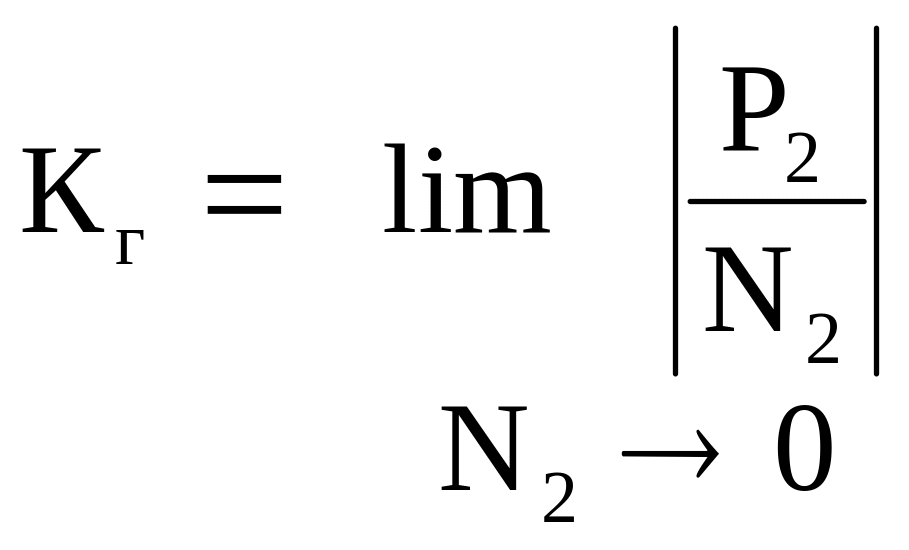(5.24)

Закон Генри установлен опытным путём для растворов газов в жидкостях. Растворимость газов в жидкостях определяет многие процессы и имеет поэтому большое практическое значение.

Если растворенное вещество – газ, то в уравнении (5.24) N₂ представляет собой растворимость газа в жидкости при парциальном давлении этого газа над раствором Р₂. Таким образом, из уравнения Генри следует, что растворимость газов в предельно разбавленных растворах пропорциональна их парциальному давлению над раствором. Количество растворенного газа чаще выражают не в молярных долях, а в единицах объёма:

V_T = K·P₂ , (5.25)

где К – коэффициент растворимости; V_T – объём газа при температуре Т. Коэффициент растворимости – это объём газа, который растворяется при данной температуре в единице объёма растворителя при парциальном давлении газа, равном единице. Если Т=273К, то уравнение (5.25) выражают через коэффициент поглощения газа К_п:

V₂₇₃ = К_п·Р₂ , (5.26)

где V₀ – объём газа, который растворяется в единице объёма растворителя при температуре 273К.

В присутствии электролитов растворимость газов уменьшается. Это явление называется высаливанием. И.М. Сеченовым получено эмпирическое уравнение, описывающее этот процесс количественно:

, (5.27)

где С⁰_Г – растворимость газа в воде, С_Г - растворимость газа в растворе электролита; С_Э – концентрация электролита.

Высаливающий эффект электролита тем больше, чем больше заряд ионов электролита и меньше их радиус: NaCl<MgCl₂<AlCl₃. Высаливающий эффект объясняется гидратацией ионов в растворе. Взаимодействия растворитель – ион связывают часть растворителя, поэтому ослабляется взаимодействие растворитель – газ, и растворимость газов падает. Поэтому растворимость газов в морской воде меньше, чем в речной. Например, растворимость О₂ в морской воде, в зависимости от солёности, от 0 до 9 мл/л; N₂ – 8,4-14,5 мл/л, при 0^оС.

В) Неидеальные (реальные) растворы. Отклонения

от закона Рауля

В реальных растворах закон Рауля не выполняется. Зависимости парциальных давлений компонентов от состава раствора не линейны и выражаются через активности компонентов в растворе а_i , зависящие от концентрации и свойств компонентов:

Р₁ = Рº₁ а₁ ; Р₂ = Рº₂ а₂ (5.28)

Наблюдаются положительные и отрицательные отклонения от закона Рауля в реальных растворах. Они обусловлены различными взаимодействиями между однородными и разнородными молекулами в растворе. Если однородные молекулы притягиваются друг к другу сильнее, чем разнородные, то это облегчает переход молекул в газовую фазу и давление повышается. Диаграмма «давление – состав жидкости» в этом случае имеет вид рис. 5.3.

Примерами таких растворов являются бензол – ацетон, вода - метиловый спирт. Их образование сопровождается поглощением тепла.

Если сильнее взаимное притяжение разнородных молекул ( сольватация, водородные связи и т.п.), то переход молекул в газовую фазу затруднён. Давление пара ниже, чем в идеальных системах, наблюдаются отрицательные отклонения от закона Рауля (рис. 5.4).

Образование таких растворов сопровождается выделением тепла. Это, например, хлороформ и ацетон.

Если отклонения от закона Рауля велики, то на кривой «давление – состав» появляется экстремум: максимум или минимум, рис.5.5.

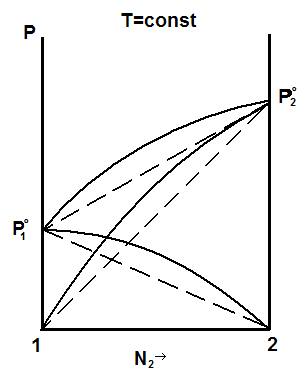
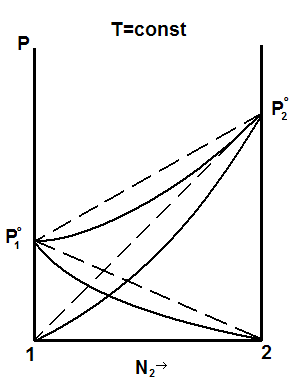
Рис. 5.3., 5.4. Диаграммы «давление – состав жидкости» при положительных и отрицательных отклонениях от закона Рауля.

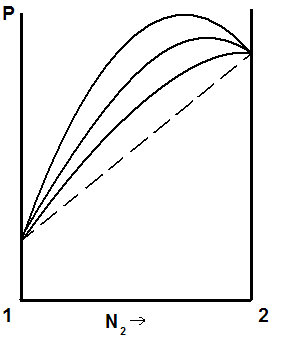
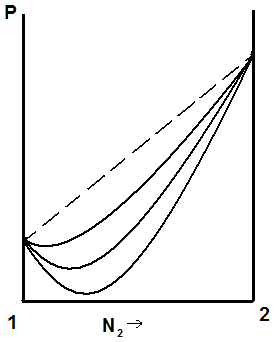
а) б)

Рис. 5.5. Кривые «давление – состав жидкости» при больших положительных (а) и отрицательных (б) отклонениях от закона Рауля