4.6. Фазовые диаграммы двухкомпонентных гетерогенных систем с эвтектикой

Рассмотрим систему, состоящую из двух компонентов А и В, которые могут находиться при условии Р = const в виде жидкого расплава компонентов и (или) твердых кристаллов индивидуальных компонентов, не образуя твердых растворов, химических соединений и полиморфных модификаций. Правило фаз Гиббса в этом случае: С = КФ+1. Так как С  0, то Ф  3, а т.к. Ф  1, то С  2. Это значит, что число фаз, которые могут находиться в равновесии, не превышает трех, а вариантность системы не более двух и при К = 2 зависит от числа равновесно сосуществующих фаз по уравнению С = 3  Ф.

Нагреем смесь компонентов А и В, имеющих определенный состав (например, 90% А и 10% В), до состояния расплава и будем следить за изменением температуры в процессе естественного охлаждения расплава. Получим кривую охлаждения, рис. 4.5, кр. 1. На участке кривой t₁t₂ происходит охлаждение расплава. При t₂ расплав становится насыщенным одним из компонентов (в данном случае  А) и начинается его кристаллизация, сопровождающаяся выделением тепла. Поэтому термограмма в точке 2 меняет угол наклона (участок t₂t₃). Расплав при этом обогащается компонентом В и при t₃ становится насыщенным и компонентом В. При этой температуре происходит одновременная кристаллизация компонентов А и В. Состав расплава, при котором компоненты кристаллизуются совместно, называется эвтектическим (от греческого  легкоплавящийся). При температуре эвтектики Ф = 3, С = 0. Кристаллизация эвтектики  изотермический процесс, т.к. состав расплава в процессе кристаллизации эвтектики не меняется. Время кристаллизации эвтектики пропорционально ее содержанию в системе. Чем ближе состав первоначально взятой смеси к эвтектическому, тем это время больше. В точке 3’ заканчивается процесс кристаллизации. Далее идет охлаждение смеси кристаллов. Сплавы, содержащие больше компонента А, называются доэвтектическими.

Их микроструктура состоит из первичных кристаллов А, окруженных затвердевшими мелкими пластинками или зернами микрокристаллов А и В в виде механической смеси.

Возьмем еще одну смесь А и В, но с меньшим относительным содержанием компонента А, чем в первой смеси. Получим такую же кривую охлаждения, но температура начала кристаллизации компонента А (t₂^/) будет на второй кривой ниже, чем на первой, т.е. расплав станет насыщенным по отношению к А при более низкой температуре.

а) б)

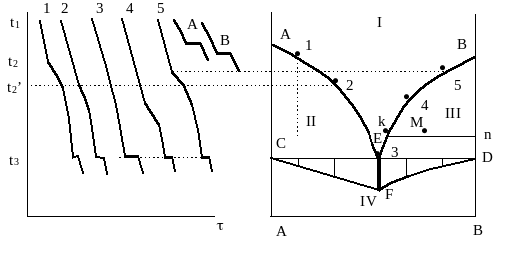
Рис. 4.5. Кривые охлаждения (а) и фазовая диаграмма (б) двухкомпонентной гетерогенной системы с эвтектикой.

Кристаллизация эвтектики не зависит от первоначального состава смеси, поэтому t₃^/ = t₃. Если компоненты А и В взять в эвтектическом соотношении, то кривая охлаждения имеет вид (кр. 3), подобный кривой охлаждения чистого индивидуального компонента.

Сплавы, содержащие больше компонента В, чем в эвтектике, называются заэвтектическими (кривые 4, 5). Здесь процесс кристаллизации начинается с компонента В и обогащения расплава компонентом А до достижения эвтектического состава. Микроструктура таких твердых фаз обратна  кристаллы В, окруженные эвтектикой. Таким образом, можно установить, какая фаза кристаллизуется первично: кристаллы А или В.

По кривым охлаждения строят фазовую диаграмму (рис. 4.5, б), перенося на нее точки начала кристаллизации компонентов в зависимости от первоначально взятого состава смеси.

Эта зависимость изобразится на диаграмме линиями АЕ и ВЕ, которые вместе образуют линию ликвидуса. Выше этой линии на диаграмме  поле однородного жидкого расплава компонентов А и В; система в этой области однофазна (гомогенна) и би-вариантна. Точка Е характеризует состав эвтектики и температуру ее кристаллизации и называется эвтектической точкой. Линия ликвидуса характеризует расплавы, насыщенные соответствующим компонентом и, в то же время,  температуру кристаллизации компонента в зависимости от состава расплава. Горизонталь CD, проходящая через точку эвтектики Е, называется линией солидуса (от греч. solidus  твердый), или эвтектической линией. Ниже линии эвтектики в системе существуют только твердые фазы  механическая смесь кристаллов А и В. Таким образом, линии ликвидуса и солидуса делят диаграмму на четыре фазовых поля:

I  поле гомогенной жидкой фазы (расплав);

II  поле двухфазного равновесия кристаллов А и расплава компонентов А и В;

III  поле двухфазного равновесия кристаллов В и расплава компонентов А и В;

IV  поле двух твердых фаз (кристаллов А и кристаллов В).

В соответствии с правилом фаз Гиббса, вариантность системы в любой точке на линии ликвидуса: С = 1, (К = 2; Ф = 2). Это означает, что только один параметр  либо температуру, либо состав  можно изменить произвольно (в некоторых пределах) так, чтобы число и характер фаз при этом не изменились. В точке эвтектики (Е) система безвариантна, С = 0, (К = 2; Ф = 3).

Это означает, что малейшее изменение любого параметра (состава системы или температуры) приведет к нарушению равновесия, и в системе произойдет изменение числа фаз или их природы.

В точке А (или В)  система однокомпонентна, двухфазна (кристаллы компонента и его расплав) и инвариантна. Инвариантность системы в точках А, В и Е объясняет постоянство температуры в процессе кристаллизации (или плавления) чистого вещества и эвтектики.

Точное положение точки эвтектики на диаграмме довольно сложно установить при изображении линии ликвидуса по экспериментальным данным.

Решить эту проблему можно, используя графическое построение  так называемый треугольник Таммана. Для этого на линии солидуса из точек, соответствующих составам смесей, взятых для снятия кривых охлаждения, наносят отрезки, соответствующие продолжительности температурных остановок в процессе кристаллизации эвтектики (см. рис. 4.5, а, кривые охлаждения). Отрезки откладывают перпендикулярно линии солидуса. Концы отрезков соединяют (треугольник CDF на рис. 4.5, б).

Для нахождения состава равновесных фаз, например, в точке М, проводят ноду kn через точку М до пересечения с линиями, ограничивающими данную гетерогенную область, параллельно оси абсцисс. Составы равновесных фаз определяют точки k и n: точка n  состав твердой фазы (кристаллы В), а точка k  состав расплава при данной температуре. Любая другая точка, лежащая на этой же ноде, будет соответствовать такому же составу фаз, как и точка М, изменятся лишь их количества. Определить количество равновесных фаз можно по правилу рычага. Например, для точки М отношение количества расплава к количеству кристаллов В равно отношению отрезков Mn / kM.

Более сложный вид имеет диаграмма с эвтектикой при наличии полиморфизма у одного из компонентов. Допустим, например, что компонент А имеет две полиморфные модификации  и . Если температура полиморфного превращения t_{  } выше температуры плавления эвтектики, диаграмма имеет вид, изображенный на рис. 4.6. Кривая охлаждения для точки М (рис. 4.6, б) имеет два изотермических участка: переход  в -модификацию и кристаллизация эвтектики. Поле I соответствует фазе  и расплаву, а поле II  фазе  и расплаву. Ниже линии солидуса  механическая смесь кристаллов В и -А.

Рис. 4.6., 4.7. Фазовые диаграммы с эвтектикой при наличии полиморфизма компонента: t_ > t_э, Рис.4.6. и t_ < t_э , Рис. 4.7

Если температура полиморфного перехода ниже температуры кристаллизации эвтектики, то диаграмма отличается от изображенной на рис. 4.5 наличием в области твердых фаз дополнительной линии t_, параллельной линии эвтектики, которая разделяет области существования кристаллов А в  (обл. I) и  (обл. II)-модификации, рис. 4.7. Горизонтальные линии, соединяющие отдельные участки на диаграммах а) и кривых охлаждения б), имеют вспомогательный характер, указывая на соответствие температур.

Многие металлы образуют между собой сплавы эвтектического типа. Это, например, алюминий и олово, медь и кадмий, серебро и таллий, серебро и висмут, кадмий и свинец.