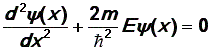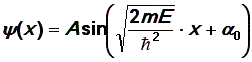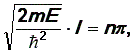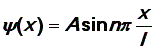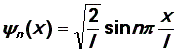81. Уравнение Шредингера для стационарных состояний. Движение свободной частицы. Электрон в потенциальном ящике.

     Основным уравнением нерелятивистской квантовой механики является временное уравнение Шредингера

     

     где 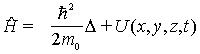- оператор полной энергии частицы (оператор Гамильтона). Это уравнение позволяет найти волновую функцию как функцию координат и времени, определить плотность вероятности нахождения частицы в любой точке пространства в любой момент времени и тем самым полностью описать квантовое состояние частицы, движущейся в силовом поле.

     В квантовой механике существует класс задач о движении в силовых полях, для которых силовая функция не зависит явно от времени, т.е. . Такие силовые поля называются стационарными силовыми полями, в этом случае силовая функция имеет смысл потенциальной энергии частицы. В стационарных полях квантовая система может находиться в состояниях с определенным значением энергии . Эти состояния называются стационарными состояниями, а задачи о движении частиц, находящихся в таких состояниях, - стационарными задачами квантовой механики.

Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенци­альная энергия частицы U(x) = const и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера (217.5) для стационарных состояний примет вид

                                                  (219.1)

Прямой подстановкой можно убедиться в том, что частным решением уравнения (219.1) является функция (х) = Ае^ikx , где А = const и k = const, с собственным значением энергии

                                                                       (219.2)

Функция  представляет собой только координатную часть волновой функции (x, t). Поэтому зависящая от времени волновая функция, согласно (217.4),

                                         (219.3)

(здесь  и ). Функция (219.3) представляет собой плоскую монохромати­ческую волну де Бройля (см. (217.2)).

Из выражения (219.2) следует, что зависимость энергии от импульса

оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое число k может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным.

Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства

т. е. все положения свободной частицы в пространстве являются равновероятными.

П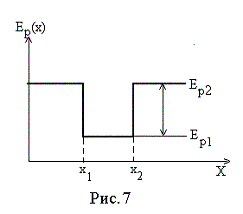 отенциальным “ящиком” называют потенциальную яму с вертикальными стенками (рис. 7). Область пространства с координатами от x₁ до x₂ на рис. 7 и есть потенциальный “ящик”. В реальной действительности такая ситуация наблюдается, например, для электронов в металле: внутри металла они свободны, но чтобы покинуть металл, электроны должны совершить работу выхода А_вых, равную

Рассмотрим простейший пример решения уравнения Шрёдингера для частицы, находящейся в потенциальном ящике с бесконечно высокими стенками (т.е. на границах ящика E_p , рис.8). Это, безусловно, идеализация. В действительности стенки ящика будут всегда конечной высоты. Однако на данной модели наиболее просто показать, что дает решение уравнения Шрёдингера. Итак, рассмотрим одномерный потенциальный ящик с бесконечно высокими стенками (рис.8). Ширина ящика l. Внутри ящика Е_p = 0, т.е. частица свободна. Уравнение Шрёдингера для этого случая примет вид:

Граничные условия: 1) при x = 0  (0) = 0, 2) при x = l  (l) = 0.

(25)     (26)

 Смысл этих условий прост: частица не может находиться на стенках ящика, так как значение Е_p =  не имеет физического смысла.

Условие нормировки:

(27)

Смысл его: частица достоверно находится внутри ящика, т.е. в области координат 0 < x < l.

Уравнения (25) – (27) полностью описывают поставленную задачу.

Решим уравнение (25). Обратите внимание, что по форме оно полностью совпадает с дифференциальным уравнением гармонических колебаний. Следовательно, и решения этих уравнений будут одинаковы:

(28)

Математически задача решена, но физического содержания решение еще не получило. Необходимо, во-первых, определить две произвольные постоянные А и ₀. Значение ₀ находим сразу из первого граничного условия:  (0) = 0, откуда ₀ = 0. Величину А найдем из условия нормировки, но сделаем это позднее. Осталось неиспользованным второе граничное условие  (l) = 0. Это возможно, если аргумент у синуса кратен  :

(29)

где n = 1, 2, 3 , … . Значение n = 0 лишено физического смысла, так как слева в уравнении (29) ни одна величина не равна нулю. Таким образом, мы пришли к выводу: решение уравнения Шрёдингера имеет физический смысл не при любых значениях энергии, а только при таких, когда выполняется условие (29), т.е. при

(30)

где n = 1, 2, 3, …  . Подставив в уравнение (28) ₀ = 0 и 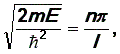получим

(31)

Из условия нормировки пси-функции найдем значение А:

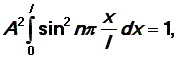
откуда Окончательно имеем набор пси-функций, зависящих от параметра n:

(32)

Вид первых четырех пси-функций представлен на рис. 9.

В еличина n характеризует значение энергии частицы и называется квантовым числом, так как энергия принимает дискретные значения, или, как говорят, квантуется.

На рис.10 показано распределение вероятности нахождения частицы в той или иной области ящика при различных значениях квантового числа n.