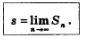Замена переменной в неопределенном интеграле

     Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:      а) , где  – монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае: ;      б) , где U – новая переменная. Формула замены переменной при такой подстановке: .      Примеры.      1. Найти интеграл .      Решение. Перепишем данный интеграл в виде . Так как производная выражения  равна 2/х, а второй множитель 1/х отличается от этой производной только постоянным коэффициентом 2, то нужно применить подстановку . Тогда . Следовательно,      .

К циклическим интегралам относятся

ʃ dx ʃ dx

ʃ dx ʃ dx В них за U можно обозначить любую из функцию сомножителей.

Билет №102. Интегрирование элементарных дробей. Разложение рациональной дроби на элементарные. Интегрирование дробно-рациональных функций.

Определение: Элементарными называются дроби следующих четырех типов:

 

  I.  III. 

 

  II.  IV. 

m, n – натуральные числа (m  2, n  2) и b² – 4ac <0.

 

  Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.

 

I.                   

 

II. 

Рассмотрим метод интегрирования элементарных дробей вида III.

Интеграл дроби вида III может быть представлен в виде:

Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.

Обозначим рациональную дробь (функцию) через , где и многочлены степени и соответственно.

Под элементарной дробью понимается дробь следующего вида:

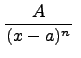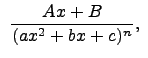   или    если

Рассмотрим случай, когда степень числителя больше или равна степени знаменателя, т.е. . Разделим многочлен на многочлен с остатком, получим, что , где -многочлен степени , - многочлен степени .

Далее заметим, что при интегрировании можно без особого труда проинтегрировать .

Хорошо известно, что многочлен можно разложить на линейные и квадратические множители. Поступим таким образом со знаменателем, т.е.

где , - степень знаменателя, т.е. многочлена . Тогда рациональная дробь разлагается на сумму элементарных дробей следующим образом:

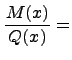
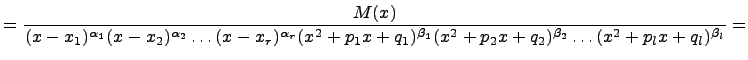
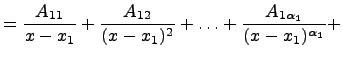
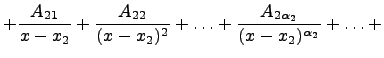
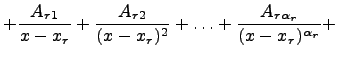
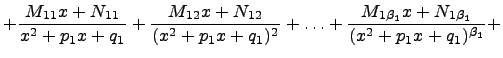
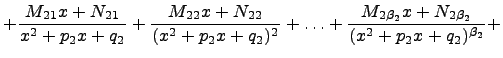
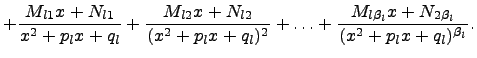
Коэффициенты , и находятся методом неопределенных коэффициентов.

Интегрирование дробно-рациональных функций

Определение 1. Функция вида , где  и - многочлены, называется дробно-рациональной функцией. Мы будем рассматривать, как правило, правильные дроби, то есть дроби , где степень многочлена в числителе меньше степени многочлена, стоящего в знаменателе. Начнем с дробей, в которых в знаменателе стоит квадратный трехчлен. Обычно дробно-рациональные функции интегрируются с помощью разложения на простейшие дроби. Проиллюстрируем этот метод несложными примерами. Пример 1. . Разложим подынтегральную функцию на простейшие дроби: . Найдем неизвестные коэффициенты  исходя из того, что после приведения правой части к общему знаменателю коэффициенты при одинаковых степенях левой и правой частей равенства должны совпадать: . Получаем равенство: = , из которого получаем систему уравнений: Решая эту линейную систему, получаем . Поэтому Пример 2. . Здесь подынтегральная функция следующим образом раскладывается на простейшие дроби: = . Получаем систему: Решая ее, получаем  значит = Билет №103. Интегрирование иррациональных и трансцендентных функций. Рассмотрим ф-ии, которые с помощью подстановки приводятся к рациональным дробям.

 

Трансцендентные функции.

Трансцендентная функция — аналитическая функция, не являющаяся алгебраической. Простейшими примерами трансцендентных функций служат показательная функция, тригонометрические функции, логарифмическая функция.

Если трансцендентные функции рассматривать как функции комплексного переменного, то характерным их признаком является наличие хотя бы одной особенности, отличной от полюсов и точек ветвления конечного порядка.

Так, например, ; и имеют существенно особую точку (где обозначает вершину сферы Римана — бесконечно удалённую точку комплексной плоскости),  — точки ветвления бесконечного порядка при и .

Основания общей теории трансцендентных функций даёт теория аналитических функций. Специальные трансцендентные функции изучаются в соответствующих дисциплинах (теория гипергеометрических, эллиптических, бесселевых функций и т. д.).

Интегрирование трансцендентных функций

 

Билет №104. Тригонометрические подстановки.

Универсальная тригонометрическая подстановка применяется при интегрировании функций рационально зависящих от sinx и cosx, т.е.

ʃ R ( sin x, cos x) dx

sin x =

аналогично получим формулу

cos x =

ʃ R ( sin x, cos x) dx = ʃ R( , ) dx =

обозначим через t – универсальная тригонометрическая подстановка.

x/2 =arctg t =

x = 2 arctg t

dx =

ʃ R( , )

Билет № 105. Задачи, приводящие к понятию определенного интеграла. Интегральные суммы. Определение и свойства определенного интеграла.

Задачи, приводящие к понятию определенного интеграла

Задача 1 (о вычислении площади криволинейной трапеции).

В декартовой прямоугольной системе координат хОу дана фигура (рис. 153), ограниченная осью х, прямыми х=а,х=Ь (а <Ъ) и графиком непрерывной и неотрицательной на отрезке [а, Ь] функции у = f(х); назовем эту фигуру криволинейной трапецией. Требуется вычислить площадь криволинейной трапеции.

Решение. Геометрия дает нам рецепты для вычисления площадей многоугольников и некоторых частей круга (сектор, сегмент). Используя геометрические соображения, мы сумеем найти лишь приближенное значение искомой площади, рассуждая следующим образом.

Разобьем отрезок [а, Ь] (основание криволинейной трапеции) на п равных частей; это разбиение осуществим с помощью точек

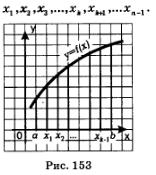
Проведем соответствующие ординаты. Тогда заданная криволинейная трапеция разобьется на n частей — на n узеньких столбиков. Площадь всей трапеции равна сумме площадей столбиков.

Рассмотрим отдельно k-тый столбик, т.е. криволинейную трапецию, основанием которой служит отрезок Заменим его прямоугольником с тем же основанием и высотой, равной f(х_к) (рис. 154). Площадь прямоугольника равна — длина отрезка ; естественно считать составленное произведение приближенным значением площади к-то столбика.

Если теперь сделать то же самое со всеми остальными столбиками, то придем к следующему результату: площадь 5 заданной криволинейной трапеции приближенно равна площади 5. ступенчатой фигуры, составленной из п прямоугольников (рис. 155). Имеем:

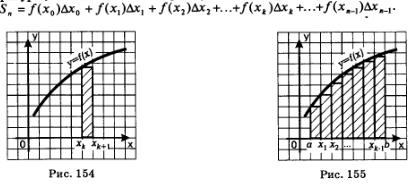
Здесь ради единообразия обозначений мы считаем, что

Итак, S = S_n, причем это приближенное равенство тем точнее, чем больше п. Принято считать, что искомая площадь есть предел последовательности Задача 2 (о вычислении массы стержня). Дан прямолинейный неоднородный стержень (рис. 156), плотность в точке х вычисляется по формуле р=р(х). Найти массу стержня. Решение. Масса тела, как известно из курса физики, равна произведению плотности на объем (вместо объема берут площадь — если речь идет о плоской пластине; вместо объема берут длину — если речь идет о прямолинейном стержне без учета его толщины). Но этот закон действует только для однородных тел, т.е. в тех случаях, когда плотность постоянна. Для неоднородного стержня используется тот же метод, что был применен при решении задачи 1.

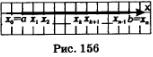1)    Разобьем отрезок [а, Ь] на п равных частей. 2)    Рассмотрим k-тый участок  и будем считать, что плотность во всех точках этого участка постоянна, а именно такая, как, например, в точке хк. Итак, мы считаем, что р = р (хк). 3)    Найдем приближенное значение массы mк к-то участка:  4)    Найдем приближенное значение массы m стержня:

5)    Точное значение массы стержня вычисляется по формуле

Задача 3 (о перемещении точки).

По прямой движется материальная точка. Зависимость скорости от времени выражается формулой v = v(t); пусть для определенности t>(f) >0. Найти перемещение точки за промежуток времени [а, Ь].

Решение. Ее ли бы движение было равномерным, то задача решалась бы очень просто: Для неравномерного движения приходится использовать те же идеи, на которых было основано решение двух предыдущих задач.

1)    Разделим промежуток времени [а, Ь] на п равных частей. 2)    Рассмотрим промежуток времени  и будем считать, что в этот промежуток времени скорость была постоянной, такой, как в момент времени. Итак, мы считаем, что v = v (t₄). 3)    Найдем приближенное значение перемещения точки зк за промежуток времени

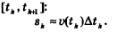  4)    Найдем приближенное значение перемещения з:

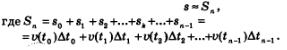5)    Точное значение перемещения вычисляется по формуле