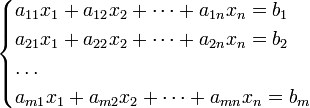- •1)Определение.
- •2)Свойства функций, непрерывных на отрезке
- •3)Теорема об обратной функции
- •1)Правила дифференцирования
- •2)Производные основных элементарных функций.
- •95 Билет: Правило Лопиталя.
- •Замена переменной в неопределенном интеграле
- •Понятие интегральной суммы
- •Определение определённого интеграла
- •Свойства определённых интегралов
Матан.
1-19.
1 Билет: Матрицы. Виды матриц. Действия с матрицами. Свойства операций с матрицами. Элементарные преобразования матриц.
Матрицы-прямоугольная таблица чисел, имеющая n-строк и n- столбцов. Обозначается большими буквами латинского алфавита.
А)Виды матриц:
-квадратная-если число строк равна числу столбцов
-единичная-диагональная матрица, у которой на главной диагонали все элементы равны единице.
-диагональная-матрица, у которой вне главной диагонали все элементы равны нулю.
-невыроженная-квадратная матрица, определитель которой не равен нулю.
-транспортированная-квадратная матрица, по отношению к данной ,если она получена путем замены строк столбцами данной матрицы.
-матрица-строка-матрица, состоящая только из одной строки.
-матрица-столбец-матрица, состоящая только из одного столбца.
-равные-2 матрицы одинакового размера-равны элементы, стоящие на одинаковых местах.
Б)Действия с матрицами. Свойства операций над матрицами
1)сложение.
Чтобы сложить 2 матрицы одинакового размера, необходимо сложить их соответствующие элементы.
2)вычитание
Определяется аналогично сложению.
3)Умножение
Пусть даны 2 матрицы разного размера. Матрицы, у которых количество столбцов первой равны числу строк второй можно перемножать. Произведение матриц не обладает свойством коммутативности, т.е переместительным законом.
Чтобы умножить матрицу на число, необходимо каждый элемент умножить на это число.
Для матриц не определено действий деления. при решения уравнения это действие можно заменить на умножение на обратную матрицу.
В)Элементарные преобразования матриц.
1)Перемена мест 2-х параллельных рядов.
2)Умножение элементов любого ряда на не равное нулю число.
3)прибавление к одному ряду линейных комбинаций других параллельных ему рядов, умноженных на любое, не равное нулю число.
4)Вычеркивание нулевой строки или нулевого столбца.
5)Вычёркивание одной из 2-х пропорциональных или равных строк.
Эти преобразования приводят матрицу к ступенчатому виду.
2 Билет: Определитель квадратной матрицы. Свойства определителя квадратной матрицы. Вычисление определителя квадратной матрицы 2-го и 3-го порядка.
Определителем
квадратной
матрицы
![]() называется
число, равное алгебраической сумме
называется
число, равное алгебраической сумме
![]() слагаемых,
каждое из которых есть произведение
слагаемых,
каждое из которых есть произведение
![]() элементов
матрицы, взятых по одному и только по
одному из каждой строки и каждого столбца
матрицы.
элементов
матрицы, взятых по одному и только по
одному из каждой строки и каждого столбца
матрицы.
Определитель
(число) квадратной матрицы порядка
![]()
![]() обозначается
символами:
обозначается
символами:
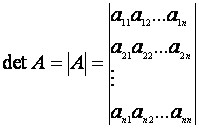 .
.
Свойства определителя:
1)Определитель не меняет своего значения.если все его строки поменять местами с соответствующими столбцами.
2)При перестановке 2-х параллельных рядов знак определителя изменяется на противоположный,а абсолютная величина остается прежней
3)Если 2 строки или 2 столбца определителя пропорциональны. то такой определитель равен нулю.
4)Если элементы какого либо ряда определителя имеют общий множитель, то его можно вынести за знак определителя.
5)Если определитель имеет нулевую строку или нулевой столбец, то он равен нулю.
6)Если элементы какого либо ряда определителя представлены суммой двух слагаемых, то определитель равен сумме 2-х определителей, у которых элементы рассматриваемого ряда равны соответствующим слагаемым.
7)Величина определителя не изменяется, если к экспонентам какого-либо ряда прибавить элементы параллельные ему ряда, предварительно умноженные на некоторое не равное нулю число.
Вычисление определителя квадратной матрицы 2-го и 3-го порядка.
1)
Правило Саррюса. |
det A = |
|
a11 |
a12 |
a13 |
|
= a11 * a22 * a33 + a12 * a23 * a31 + a13 * a21 * a32 - a13 * a22 * a31 - a12 * a21 * a33 - a11 * a23 * a32 |
a21 |
a22 |
a23 |
||||
a31 |
a32 |
a33 |
det A = |
|
4 |
-2 |
4 |
|
= |
10 |
2 |
12 |
||||
1 |
2 |
2 |
= 4 * 2 * 2 + ( -2) * 12 * 1 + 4 * 10 * 2 - 4 * 2 * 1 - ( -2) * 10 * 2 - 4 * 12 * 2 = 8
Из общего правила вычисления определителя легко получить частные формулы для вычисления определителей любого порядка. Так для определителя 2-го порядка получаем следующую формулу:
Аналогично для определителя 3-го порядка :
|
3 Билет: Миноры и алгебраические дополнения элементов матриц. Вычисление определителя квадратной матрицы разложение элементов строки или столбца.
Минор элемента определителя 3-го порядка-определитель 2-го порядка ,полученный из данного вычёркиванием строки и столбца на пересечении которых стоит данный элемент.
Алгебраические дополнения элемента определителя- минор этого элемента , взятый со знаком +, если сумма индексов элемента чётная, и со знаком - ,если сумма нечётная.
Алгебраическим
дополнением элемента
![]() матрицы
называется
число, равное произведению минора этого
элемента на
матрицы
называется
число, равное произведению минора этого
элемента на
![]()
![]()
Теорема разложения.
Определитель 3-го порядка равен сумме произведения какого-либо ряда на их соответствующие алгебраические дополнения.
*Замечание1: Для упрощения вычисления определителя применяют 7 свойство для накопления нулей в определителе.
*Замечание 2: Определители , имеющие количество строк и столбцов более 3-х называются определителями высших порядков. Для их вычисления применяют теорему разложения.
4 Билет: Невыроженные матрицы. Присоединённая матрица. Обратная матрица. Нахождение обратной матрицы с помощью присоединённой матрицы.
Невыроженные матрицы- квадратная матрица, определитель которой не равен нулю.
Присоединённая матрица- квадратная матрица, образованная алгебраическими дополнениями к элементам матрицы, полученной из исходной транспонированием.
Обратная матрица- такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
![]()
Обратная матрица матрице А, обозначается через А1, так что В = А1 и вычисляется по формуле
 ,
(1)
,
(1)
где А i j - алгебраические дополнения элементов a i j матрицы A..
Δ =det A.
Алгоритм нахождения обратной матрицы.
1)Вычислить определитель матриц и убедиться, что он не равен нулю.
2)Находим алгебраические дополнения элементов матрицы и составляем присоединенную матрицу.
3)С помощью формулы находим обратную матрицу.
4)Делаем проверку
5 Билет:Нахождения обратной матрицы с помощью элементарных преобразований.
Элементарными преобразованиями над матрицей называются:
1)умножение любой строки на число, отличное от нуля;
2)прибавление к элементам одной строки соответствующих элементов другой, умноженных на одно и то же число;
3) перестановка строк;
4) отбрасывание строки из нулей.
Пусть А - исходная матрица, обратную к которой мы хотим найти.
n и k - кол-во строк и столбцов в ней соотвественно.
Сначала проверим является ли А квадратной, т.е. совпадают ли n и k.
Затем проверим равен ли определитель мартицы А нулю. Если он равен нулю, то обратной матрицы не существует.
Создаем матрицу Inv равную единичной размерности nxn.
А затем при помощи элементарных преобразований: сложения строк матрицы, умножения строки на число, перестановки столбцов и строк приведем матрицу A к единичной. Причем, параллельно, те же самые преобразования будем производить и с матрицей Inv (переставлять и складывать те же строки/столбцы, и умножать на это же число).
В результате, матрица Inv - будет являться обратной матрицей к исходной матрице A.
6 Билет: Матричные уравнения и методы их решения.
Системой
m
линейных уравнений с n
неизвестными
![]() называется
система S
вида
называется
система S
вида
 ,
,
где
![]() коэффициенты
при неизвестных,
коэффициенты
при неизвестных,
![]() свободные
члены (
,
свободные
члены (
,
![]() заданные
числа).
заданные
числа).
Определение
5.2.
Решением системы
![]() называется
упорядоченный набор действительных
чисел
называется
упорядоченный набор действительных
чисел
![]() ,
при подстановке которых в каждое
уравнение системы вместо
,
при подстановке которых в каждое
уравнение системы вместо
![]() соответственно
будут получены верные числовые равенства.
соответственно
будут получены верные числовые равенства.
Определение
5.3.
Система
![]() называется
совместной (несовместной), если она
имеет хотя бы одно решение (не имеет
решений).
называется
совместной (несовместной), если она
имеет хотя бы одно решение (не имеет
решений).
Определение 5.4. Совместная система линейных алгебраических уравнений называется определённой (неопределённой), если она имеет единственное решение (множество решений).
Определение
5.5.
Матрица
![]() ,
составленная из коэффициентов при
неизвестных, называется основной
матрицей системы
:
,
составленная из коэффициентов при
неизвестных, называется основной
матрицей системы
:

Матрица

называется расширенной матрицей этой системы.
Замечание. Система может быть переписана в так называемом матричном виде:
![]()
где
![]() вектор-столбец
свободных членов системы.
вектор-столбец
свободных членов системы.
Определение 5.6. Если все свободные члены системы уравнений равны нулю, то такая система называется однородной, если же хотя бы один свободный член отличен от нуля, система называется неоднородной.
Теорема 5.1. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда определитель основной матрицы системы равен нулю.
Определение 5.7. Элементарными преобразованиями системы линейных уравнений называют следующие операции:
1) сложение обеих частей одного уравнения с соответствующими частями другого, умноженных на одно и то же число, не равное нулю;
2) перестановка уравнений местами;
3) удаление из системы уравнений, являющихся тождествами.
Рассмотрим основные методы решения систем линейных уравнений.
Метод Гаусса
Метод Крамера
Матричный метод решения систем линейных уравнений
7 Билет: Понятие ранга матрицы. Ранг ступенчатой матрицы. Теорема о ранге.
Ранг матрицы-наивысший порядок минора , отличного от нуля и обозначается Ra.В этом случае минор называется Базисным.
Ранг ступенчатой матрицы равен количеству её ненулевых строк.
Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А).
Теорема
Кронекера–Капелли (критерий совместности
системы линейных уравнений). Для того
чтобы система линейных уравнений была
совместной, необходимо и достаточно,
чтобы ранг матрицы системы был равен
рангу ее расширенной матрицы, т.е.
![]() .
.
Замечание. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений.
8 Билет: Вычисление ранга матрицы с помощью элементарных преобразований.
элементарными преобразованиями матриц следующие действия над ними: 1) перестановка строк или столбцов; 2) умножение строки или столбца на число отличное от нуля; 3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.
9 Билет: Система линейных алгебраических уравнений. Решение системы линейных алгебраических уравнений. Классификация систем линейных алгебраических уравнений.
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
Решение системы — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Классификация систем линейных алгебраических уравнений.
1)Однородная-все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
2)Квадратная-если число m уравнений равно числу n неизвестных.
3)Совместная- если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
10 Билет : Метод Гаусса. Решение систем линейных алгебраических уравнений. Общие частные систем линейных алгебраических уравнений
|
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Пусть исходная система выглядит следующим образом
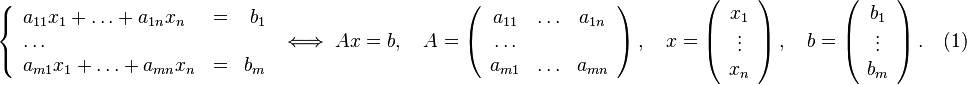
Матрица
![]() называется
основной матрицей системы,
называется
основной матрицей системы,
![]() —
столбцом свободных членов.
—
столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):
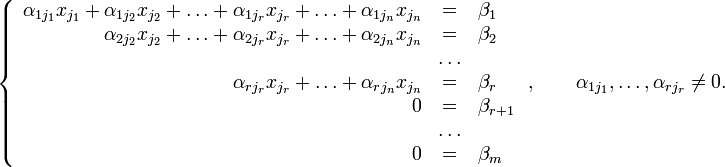 При этом будем
считать, что базисный
минор
(ненулевой минор
максимального порядка) основной матрицы
находится в верхнем левом углу, то есть
в него входят только коэффициенты при
переменных
При этом будем
считать, что базисный
минор
(ненулевой минор
максимального порядка) основной матрицы
находится в верхнем левом углу, то есть
в него входят только коэффициенты при
переменных
![]() [3].
[3].
Тогда переменные называются главными переменными. Все остальные называются свободными.
Если
хотя бы одно число
![]() ,
где
,
где
![]() ,
то рассматриваемая система несовместна,
т.е. у неё нет ни одного решения.
,
то рассматриваемая система несовместна,
т.е. у неё нет ни одного решения.
Пусть
![]() для
любых
.
для
любых
.
Перенесём
свободные переменные за знаки равенств
и поделим каждое из уравнений системы
на свой коэффициент при самом левом
![]() (
(![]() ,
где
,
где
![]() —
номер строки):
—
номер строки):
 ,
где
,
где
![]()
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
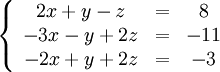
Обнулим
коэффициенты при
во
второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на
![]() и
и
![]() ,
соответственно:
,
соответственно:
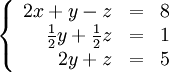
Теперь
обнулим коэффициент при
![]() в
третьей строке, вычтя из неё вторую
строку, умноженную на
в
третьей строке, вычтя из неё вторую
строку, умноженную на
![]() :
:
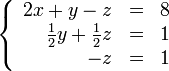
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
![]() из
третьего;
из
третьего;
![]() из
второго, подставив полученное
из
второго, подставив полученное
![]()
![]() из
первого, подставив полученные
и
.
из
первого, подставив полученные
и
.
Таким образом исходная система решена.
Билет 11: Метод крамера. Решение систем линейных алгебраических уравнений.
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).
Описание метода
Для
системы
![]() линейных
уравнений с
неизвестными
(над произвольным полем)
линейных
уравнений с
неизвестными
(над произвольным полем)
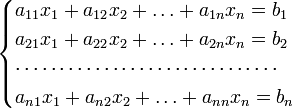
с
определителем матрицы системы
![]() ,
отличным от нуля, решение записывается
в виде
,
отличным от нуля, решение записывается
в виде
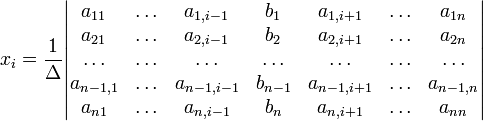
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
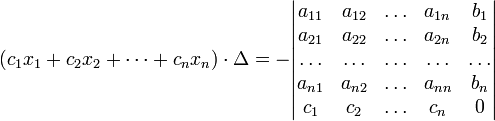
В
этой форме формула Крамера справедлива
без предположения, что
отлично
от нуля, не нужно даже, чтобы коэффициенты
системы были бы элементами
целостного
кольца (определитель системы может
быть даже делителем нуля в кольце
коэффициентов). Можно также считать,
что либо наборы
![]() и
и
![]() ,
либо набор
,
либо набор
![]() состоят
не из элементов кольца коэффициентов
системы, а какого-нибудь модуля
над этим кольцом. В этом виде формула
Крамера используется, например, при
доказательстве формулы для определителя
Грама и Леммы
Накаямы.
состоят
не из элементов кольца коэффициентов
системы, а какого-нибудь модуля
над этим кольцом. В этом виде формула
Крамера используется, например, при
доказательстве формулы для определителя
Грама и Леммы
Накаямы.
Пример
Система линейных уравнений:
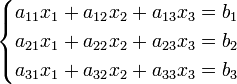
Определители:
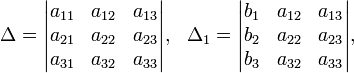
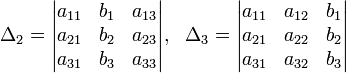
Решение:
![]()
Пример:
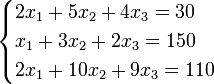
Определители:
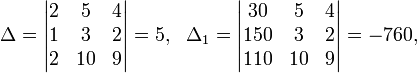
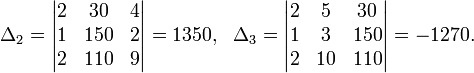
![]()
12 Билет : Матричный Метод решения систем линейных алгебраических уравнений.
Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:
![]() ,
где
—
основная матрица системы,
,
где
—
основная матрица системы,
![]() и
и
![]() —
столбцы свободных членов и решений
системы соответственно:
—
столбцы свободных членов и решений
системы соответственно:
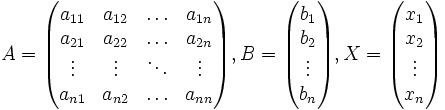
Умножим
это матричное уравнение слева на
![]() —
матрицу, обратную к матрице
:
—
матрицу, обратную к матрице
:
![]()
Так
как
![]() ,
получаем
,
получаем
![]() .
Правая часть этого уравнения даст
столбец решений исходной системы.
Условием применимости данного метода
(как и вообще существования решения
неоднородной системы линейных уравнений
с числом уравнений, равным числу
неизвестных) является невырожденность
матрицы A. Необходимым и достаточным
условием этого является неравенство
нулю определителя
матрицы A:
.
Правая часть этого уравнения даст
столбец решений исходной системы.
Условием применимости данного метода
(как и вообще существования решения
неоднородной системы линейных уравнений
с числом уравнений, равным числу
неизвестных) является невырожденность
матрицы A. Необходимым и достаточным
условием этого является неравенство
нулю определителя
матрицы A:
![]() .
.
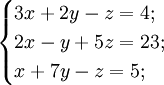
Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ (система линейных алгебраических уравнений) не равен нулю.
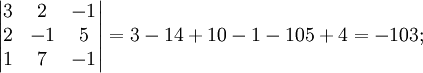
Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.
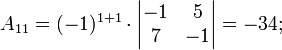
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.
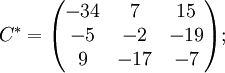
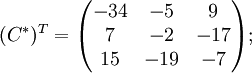
![]()
Подставляя переменные в формулу, получаем:
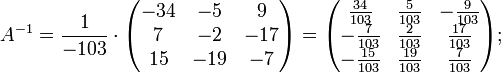
Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.
![]()
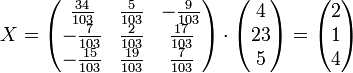
Итак, x=2; y=1; z=4.
13 Билет: Задачи исследования систем линейных алгебраических уравнений. Совместность однородных систем алгебраических уравнений. Критерий совместимости систем линейных алгебраических уравнений.
При исследовании систем линейных уравнений решаются следующие задачи:
является ли система совместной;
если система совместна, то определенна или неопределенна (критерий совместности системы определяется по теореме);
если система определенна, то как найти ее единственное решение (используются метод Крамера, метод обратной матрицы или метод Жордана-Гаусса);
если система неопределенна, то как описать множество ее решений.
Система
уравнений называется совместной, если
она имеет хотя бы одно решение, и
несовместной, если она не имеет ни одного
решения.
Система линейных уравнений
называется однородной, если все свободные
члены равны нулю:
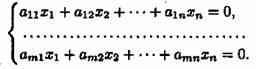 Однородная
система всегда совместна, так как
x1=x2=x3=…=xn=0 является решением системы.
Это решение называется нулевым или
тривиальным.
Однородная
система всегда совместна, так как
x1=x2=x3=…=xn=0 является решением системы.
Это решение называется нулевым или
тривиальным.
Критерий совместимости систем линейных алгебраических уравнений.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу матрицы системы.
Это утверждение называют теоремой Кронекера-Капелли.
16 Билет: Различные подходы к определению понятия вектора. Линейные операции с векторами и их свойства.
1)Вектором![]() называется
семейство всех параллельных между собой
одинаково направленных и имеющих
одинаковую длину отрезков (рис.1).
называется
семейство всех параллельных между собой
одинаково направленных и имеющих
одинаковую длину отрезков (рис.1).

Вектор
изображают на чертежах отрезком со
стрелкой (т.е. изображают не все семейство
отрезков, представляющее собой вектор,
а лишь один из этих отрезков). Для
обозначения векторов в книгах и статьях
применяют жирные латинские буквы а,
в, с
и так далее, а в тетрадях и на доске –
латинские буквы с черточкой сверху,
![]()
![]()
![]()
Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой без черточки) обозначают длину вектора. Длину иногда обозначают также вертикальными черточками – как модуль (абсолютную величину) числа. Таким образом, длина вектора а обозначается через а или IаI, а в рукописном тексте длина вектора обозначается через а или IаI. В связи с изображением векторов в виде отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор, неравноправны: одного конца отрезка к другому.

Различают начало и конец вектора (точнее, отрезка, изображающего вектор).
2) Вектором называется направленный отрезок. При этом векторы (т.е. направленные отрезки), имеющие одинаковую длину и одно и то же направление (рис.3), уславливаются считать равными.

Векторы называются одинаково направленными, если их полупрямые одинаково направлены.
Линейные операции с векторами и их свойства.
Операция сложения двух векторов - правило треугольника.
Покажем как происходит сложение двух векторов.
Сложение
векторов
![]() и
и
![]() происходит
так: от произвольной точки A
откладывается вектор
происходит
так: от произвольной точки A
откладывается вектор
![]() ,
равный
,
далее от точки B
откладываеься вектор
,
равный
,
далее от точки B
откладываеься вектор
![]() ,
равный
,
и вектор
,
равный
,
и вектор
![]() представляет
собой сумму
векторов
и
.
Такой способ сложения двух векторов
назвается правилом
треугольника.
представляет
собой сумму
векторов
и
.
Такой способ сложения двух векторов
назвается правилом
треугольника.
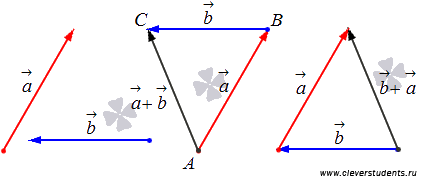
Проиллюстрируем сложение не коллинеарных векторов на плоскости по правилу треугольника.
А на чертеже ниже показано сложение сонаправленных и противоположно направленных векторов.

Операция вычитания двух векторов .
Чтобы из вектора а вычесть вектор b надо к вектору а прибавить вектор, противоположный вектору b. Полученный в результате этой операции вектор с и будет являться разностью векторов а и b. Таким образом,
с = а − b = а + (− b).
Рисунок 5 иллюстрирует операцию вычитания векторов.

Рис. 5
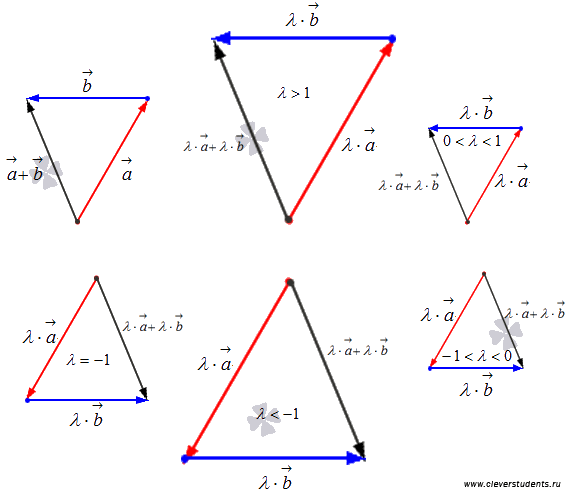
Операция умножения вектора на число.
Сейчас разберемся как происходит умножение вектора на число.
Умножение
вектора на число k
соответствует растяжению вектора в k
раз при k > 1
или сжатию в
![]() раз
при 0 < k < 1,
при k = 1
вектор остается прежним (для отрицательных
k
еще изменяется направление на
противоположное). Если произвольный
вектор умножить на ноль, то получим
нулевой вектор. Произведение нулевого
вектора и произвольного числа есть
нулевой вектор.
раз
при 0 < k < 1,
при k = 1
вектор остается прежним (для отрицательных
k
еще изменяется направление на
противоположное). Если произвольный
вектор умножить на ноль, то получим
нулевой вектор. Произведение нулевого
вектора и произвольного числа есть
нулевой вектор.
К примеру, при умножении вектора на число 2 нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное. Приведем для наглядности иллюстрацию этого случая.
Свойства операций над векторами.
Итак,
мы определили операцию сложения векторов
и операцию умножения вектора на число.
При этом для любых векторов
![]() и
произвольных действительных чисел
и
произвольных действительных чисел
![]() можно
при помощи геометрических построений
обосновать следующие свойства
операций над векторами.
Некоторые из них очевидны.
можно
при помощи геометрических построений
обосновать следующие свойства
операций над векторами.
Некоторые из них очевидны.
Свойство
коммутативности
![]() .
.
Свойство
ассоциативности сложения
![]() .
.
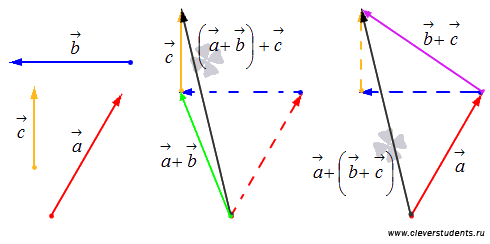
Существует
нейтральный элемент по сложению, которым
является нулевой вектор
![]() ,
и
,
и
![]() .
Это свойство очевидно.
.
Это свойство очевидно.
Для
любого ненулевого вектора
существует
противоположный вектор
![]() и
верно равенство
и
верно равенство
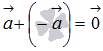 .
Это свойство очевидно без иллюстрации.
.
Это свойство очевидно без иллюстрации.
Сочетательное
свойство умножения
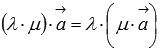 .
К примеру, растяжение вектора в 6 раз
можно произвести, если сначала его
растянуть вдвое и полученный вектор
растянуть еще втрое. Аналогичного
результата можно добиться, например,
сжав вектор вдвое, а полученный вектор
растянуть в 12
раз.
.
К примеру, растяжение вектора в 6 раз
можно произвести, если сначала его
растянуть вдвое и полученный вектор
растянуть еще втрое. Аналогичного
результата можно добиться, например,
сжав вектор вдвое, а полученный вектор
растянуть в 12
раз.
Первое
распределительное свойство
![]() .
Это свойство достаточно очевидно.
.
Это свойство достаточно очевидно.
Второе
распределительное свойство
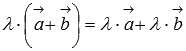 .
Это свойство справедливо в силу подобия
треугольников, изображенных ниже.
.
Это свойство справедливо в силу подобия
треугольников, изображенных ниже.
Нейтральным
числом по умножению является единица,
то есть,
![]() .
При умножении вектора на единицу с ним
не производится никаких геометрических
преобразований.
.
При умножении вектора на единицу с ним
не производится никаких геометрических
преобразований.
17 Билет: Линейная зависимость и линейная независимость системы векторов.
Рассмотрим
набор из p
n-мерных
векторов,
обозначим их следующим образом
![]() .
Составим линейную комбинацию этих
векторов и произвольных чисел
.
Составим линейную комбинацию этих
векторов и произвольных чисел
![]() (действительных
или комплексных):
(действительных
или комплексных):
![]() .
Отталкиваясь от определения операций
над n-мерными
векторами, а так же свойств операций
сложения векторов и умножения вектора
на число, можно утверждать, что записанная
линейная комбинация представляет собой
некоторый n-мерный
вектор
.
Отталкиваясь от определения операций
над n-мерными
векторами, а так же свойств операций
сложения векторов и умножения вектора
на число, можно утверждать, что записанная
линейная комбинация представляет собой
некоторый n-мерный
вектор
![]() ,
то есть,
,
то есть,
![]() .
.
Так мы подошли к определению линейной зависимости системы векторов .
Определение.
Если линейная комбинация может представлять собой нулевой вектор тогда, когда среди чисел есть хотя бы одно, отличное от нуля, то система векторов называется линейно зависимой.
Определение.
Если линейная комбинация представляет собой нулевой вектор только тогда, когда все числа равны нулю, то система векторов называется линейно независимой.
18 Билет: Базис системы векторов.
Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.
Базис системы векторов
Базисом системы векторов A1 , A2 ,..., An называется такая подсистема B1, B2 ,...,Br (каждый из векторов B1,B2,...,Br является одним из векторов A1 , A2 ,..., An), которая удовлетворяет следующим условиям: 1. B1,B2,...,Br линейно независимая система векторов; 2. любой вектор Aj системы A1 , A2 ,..., An линейно выражается через векторы B1,B2,...,Br
r — число векторов входящих в базис.
Теорема О единичном базисе системы векторов.
Если система m-мерных векторов содержит m различных единичных векторов E1 E2 ,..., Em , то они образуют базис системы.
19 Билет: Скалярное произведение векторов и его свойства. Вычисление угла между векторами.
Определение скалярного произведения
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.
Обозначается ab,а* b(или( а, b)).Итак, по определению,
![]()
![]()
Формуле (6.1) можно придать иной вид. Так как | a| cos=пр ba, (см. рис.14), a |b| cos = пр ab, то получаем:
![]()
т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства скалярного произведения
1.
Скалярное произведение обладает
переместительным свойством: ab=ba
 Решение:
Решение:
![]()
![]()
5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0 b, то а b
.
Угол между векторами
Определение угла φ между ненулевыми векторами а = (ax; ay; az) и b=( bх; bу; bг):
![]()
Отсюда следует условие перпендикулярности ненулевых векторов а и b:
![]()
Билет № 20
 Векторным
произведение векторов a
и b
называется такой вектор с, который
обладает св-ми:
Векторным
произведение векторов a
и b
называется такой вектор с, который
обладает св-ми:
1. ICI = IaI * IbI * sin(a^b)

 2.
c
a,
c
b.
2.
c
a,
c
b.
3. Векторы a,b,c образуют правую тройку (обозначается) с = a * b
(a, b) – скалярное.
[a, b] – векторное.
Свойства
1.Векторное
произведение ![]() равно
нулю, если векторы
равно
нулю, если векторы ![]() и
и ![]() коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2.
При перестановке местами векторов
сомножителей векторное произведение
меняет знак на противоположный (см.
рисунок):
![]()
![]()
![]() (синус
не четная функция)
(синус
не четная функция)
3.(α a) * (β b) = α*β (a*b)
4.(a + b) * c = a*c + b*c
5. Из определения векторного произведения и элементарной геометрии следует, что площадь параллелограмма построенного на векторах a и b, численно равна модулю векторного произведения.


Вычисление площади треугольника
Решение Найти площадь треугольника если А(1;2;3), B(2;2;2), C(1;2;4)
 1.Выбираем точку
с которой будут выходить векторы.
1.Выбираем точку
с которой будут выходить векторы.
AB{2-1;2-2;2-3} ={1;0;-1}. AC= {1-1;2-2;4-3} = {0;0;1}
Билет № 21
Смешанным или векторно - скалярным произведением трех векторов называется число равное скалярному произведению (a*b) * c, обозначается = abc.
![]() .
Смешанное произведение равно нулю тогда
и только тогда, когда сомножители
компланарны.
.
Смешанное произведение равно нулю тогда
и только тогда, когда сомножители
компланарны.
![]() .
Модуль смешанного произведения
некомпланарных векторов численно равен
объему параллелепипеда, построенного
на сомножителях. Если
.
Модуль смешанного произведения
некомпланарных векторов численно равен
объему параллелепипеда, построенного
на сомножителях. Если ![]() ---
правая тройка, то
---
правая тройка, то ![]() ;
в противном случае (т.е. когда эта тройка
левая)
;
в противном случае (т.е. когда эта тройка
левая) ![]() .
.
![]() .
. ![]() :
:
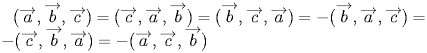 Абсолютная
величина смешанного произведения
векторов = объёму параллепипеда
построенного на этих сторонах,то есть
Vпар.
= IabcI.
Vпар
=
Абсолютная
величина смешанного произведения
векторов = объёму параллепипеда
построенного на этих сторонах,то есть
Vпар.
= IabcI.
Vпар
=
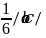 .
.
Билет № 23
Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем является прямоугольная (декартова) система координат.
Прямоугольная система
координат задается двумя взаимно
перпендикулярными прямыми — осями, на
каждой из которых выбрано положительное
направление и задан единичный (масштабный)
отрезок. Единицу масштаба обычно
берут одинаковой для обеих осей. Эти
оси называют осями координат, точку их
пересечения О - началом координат.
Одну из осей называют осью абсцисс (осью
Ох), другую — осью ординат (осью Оу) (рис.
23).

На рисунках ось абсцисс обычно располагают горизонтально и направленной слева направо, а ось ординат - вертикально и направленной снизу вверх. Оси координат делят плоскость на четыре области — четверти (или квадранты).
Единичные
векторы осей обозначают i и j(| i |=| j |=1, ![]() ).
Систему координат обозначают Оху, а
плоскость, в которой расположена
).
Систему координат обозначают Оху, а
плоскость, в которой расположена
система координат, называют координатной плоскостью.
Рассмотрим произвольную точку Μ плоскости Оху. Вектор ОМ называется радиусом-вектором точки М.
Координатами точки Μ в системе координат Оху называются координаты радиуса-вектора OM. ЕслиOM=(x;y), то координаты точки Μ записывают так: М(х;у), число x называется абсциссой точки М, у —ординатой точки Μ.
Эти два числа x и y полностью определяют положение точки на плоскости, а именно: каждой паре чисел и y соответствует единственная точка М плоскости, и наоборот.
Билет №24
 Другой
практически важной системой
координат является полярная система
координат. Полярная система координат
задается точкой О, называемой полюсом,
лучом Ор, называемым полярной осью,
иединичным
вектором e того
же направления, что и луч Ор.
Другой
практически важной системой
координат является полярная система
координат. Полярная система координат
задается точкой О, называемой полюсом,
лучом Ор, называемым полярной осью,
иединичным
вектором e того
же направления, что и луч Ор.
Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием г от полюса О и углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24).
2. Возведем в квадрат все части уравнения.
Билет № 26
Линия на плоскости рассматривается (задается) как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, окружность радиуса R есть множество всех точек плоскости, удаленных на расстояние - R от некоторой фиксированной точки О (центра окружности).
Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x;y) = 0 с двумя переменными, которому удовлетворяют координаты x и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
 - окружность
- окружность
 = 1
– эллипс
= 1
– эллипс
Ур. Гиперболы. Ур. Параболы.
Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0 причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки:
![]()
Уравнение прямой по точке и вектору нормали
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Пример.
Найти уравнение прямой, проходящей
через точку А(1, 2) перпендикулярно
вектору ![]() (3,
-1).
(3,
-1).
Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой по точке и угловому коэффициенту
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
![]()
Уравнение прямой в отрезках
Если
в общем уравнении прямой Ах + Ву + С = 0
С≠0, то, разделив на –С, получим: ![]() или
или
![]() ,
где
,
где![]() Геометрический
смысл коэффициентов в том, что
коэффициент а является
координатой точки пересечения прямой
с осью Ох, а b –
координатой точки пересечения прямой
с осью Оу.
Геометрический
смысл коэффициентов в том, что
коэффициент а является
координатой точки пересечения прямой
с осью Ох, а b –
координатой точки пересечения прямой
с осью Оу.
Билет №27
Взаимное расположение двух прямых на плоскости
Если две прямые l1 и l2 лежат на плоскости, то возможны три различных случая их взаимного расположения: 1)пересекаются (т.е. имеют одну общую точку); 2) параллельны и не совпадают; 3) совпадают.
Выясним, как узнать, какой из этих случаев имеет место, если эти прямые заданы своими уравнениями в общем виде:
![]() (12)
(12)
Если прямые l1 и l2 пересекаются в некоторой точке М(х,у), то координаты этой точки должны удовлетворять обоим уравнениям системы (12).
Следовательно, чтобы найти координаты точки пересечения прямых l1 и l2, надо решить систему уравнений (12): 1) если система (12) имеет единственное решение, то прямые l1 и l2 пересекаются; 2) если система (12) не имеет решения, то прямые l1 и l2 параллельны; 3) если система (12) имеет множество решений, то прямые l1 и l2 совпадают.
Условием совпадения двух прямых является пропорциональность соответствующих коэффициентов их уравнений.
Угол между прямыми
За угол между двумя прямыми в пространстве принимают один из двух смежных углов, который образует прямые, проведенные параллельно данным через какую-нибудь точку в пространстве.
Один из этих углов равен углу между направляющими векторами этих прямых.
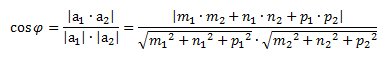
Где первая прямая задается:
![]()
а1=( m1, n1, p1)
Вторая прямая задается:
![]()
а2=( m2, n2, p2)
Если прямые параллельны, то
![]()
Билет №28
Общее уравнение кривой второго порядка
![]()
Уравнение такого вида может определять: 1) эллипс (в частности, окружность), 2) гиперболу, 3) параболу, 4) пару прямых (параллельных, пересекающихся либо совпадающих), 5) точку или не определять никакой линии.
В простейшем случае, при В = 0, тип кривой можно определить, выделив полные квадраты переменных.
Билет №30
Эллипс - это геометрическая фигура, которая ограничена кривой, заданной уравнением .
![]() .
.

Фокусное расстояние и полуоси связаны соотношением:
a2 = b 2 + c 2.
Доказательство: В
случае, если точка М находится на
пересечении эллипса с вертикальной
осью, r1 +
r2 =
2*![]() (по
теореме Пифагора). В случае, если точка
М находится на пересечении его с
горизонтальной осью, r1 +
r 2 =
a – c + a + c. Т.к. по определению сумма r1 +
r 2 –
постоянная величина, то , приравнивая,
получаем:
(по
теореме Пифагора). В случае, если точка
М находится на пересечении его с
горизонтальной осью, r1 +
r 2 =
a – c + a + c. Т.к. по определению сумма r1 +
r 2 –
постоянная величина, то , приравнивая,
получаем:
a 2 = b 2 + c 2
r1 + r2 = 2 a .
Эксцентриситет фигуры эллипс
Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .
е = с/ a .
Т.к. с < a , то е < 1.
Определение. Величина k = b / a называется коэффициентом сжатия , а величина 1 – k = ( a – b )/ a называется сжатием.
Коэффициент сжатия и эксцентриситет связаны соотношением: k2 = 1 – e 2 .
Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.
Если
для точки М(х 1 ,
у 1 )
выполняется условие: ![]() ,
то она находится внутри эллипса, а
если
,
то она находится внутри эллипса, а
если ![]() ,
то точка находится вне его.
,
то точка находится вне его.
Теорема. Для произвольной точки М(х, у), принадлежащей фигуре эллипс верны соотношения :
r 1 = a – ex , r2 = a + ex .
Билет № 31
Гиперболой называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек F1 и F2 , называемых фокусами гиперболы, есть величина постоянная.
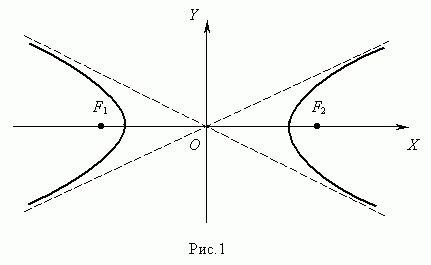
Уравнение гиперболы
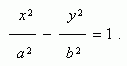
Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии.
Отрезок F1F2 =
2 с ,
где ![]() ,
называется фокусным
расстоянием.
Отрезок AB =
2 a называется действительной
осью гиперболы,
а отрезок CD =
2 b – мнимой
осью гиперболы.
Число e = c / a , e >
1 называется эксцентриситетом гиперболы.
Прямые y = ( b / a ) x называютсяасимптотами
гиперболы.
,
называется фокусным
расстоянием.
Отрезок AB =
2 a называется действительной
осью гиперболы,
а отрезок CD =
2 b – мнимой
осью гиперболы.
Число e = c / a , e >
1 называется эксцентриситетом гиперболы.
Прямые y = ( b / a ) x называютсяасимптотами
гиперболы.
Пусть Р ( х1 , у 1 ) – точка гиперболы, тогда уравнение касательной к гиперболе в данной точке имеет вид:
![]()
Условие касания прямой y = m x + k и гиперболы х 2 / a 2 – у 2 / b 2 = 1 :
k 2 = m 2 a 2 – b 2 .
Билет № 32
Парабола-называется геометрическое место точек плоскости, равноудаленных от заданной точки и заданной прямой , не проходящей через заданную точку. Это геометрическое определение выражает директориальное свойство параболы.
Точка ![]() называется
фокусом параболы, прямая
называется
фокусом параболы, прямая ![]() —
директрисой параболы, середина
—
директрисой параболы, середина ![]() перпендикуляра,
опущенного из фокуса на директрису, —
вершиной параболы, расстояние
перпендикуляра,
опущенного из фокуса на директрису, —
вершиной параболы, расстояние ![]() от
фокуса до директрисы — параметром
параболы, а расстояние
от
фокуса до директрисы — параметром
параболы, а расстояние ![]() от
вершины параболы до её фокуса — фокусным
расстоянием (рис.3.45,а). Прямая,
перпендикулярная директрисе и проходящая
через фокус, называется осью параболы
(фокальной осью параболы). Отрезок
от
вершины параболы до её фокуса — фокусным
расстоянием (рис.3.45,а). Прямая,
перпендикулярная директрисе и проходящая
через фокус, называется осью параболы
(фокальной осью параболы). Отрезок![]() ,
соединяющий произвольную точку
,
соединяющий произвольную точку ![]() параболы
с её фокусом, называется фокальным
радиусом точки
.
Отрезок, соединяющий две точки параболы,
называется хордой параболы.
параболы
с её фокусом, называется фокальным
радиусом точки
.
Отрезок, соединяющий две точки параболы,
называется хордой параболы.
Билет №35
Дано
уравнение ![]() .
Определить тип кривой, ее параметры и
сделать рисунок.
Сгруппируем
переменные:
.
Определить тип кривой, ее параметры и
сделать рисунок.
Сгруппируем
переменные:
![]() Дополним
выражения, стоящие в скобках, до полного
квадрата:
Дополним
выражения, стоящие в скобках, до полного
квадрата:
![]() Учитывая
Учитывая ![]() ,
получим:
,
получим:
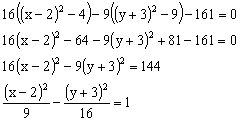 Уравнение
Уравнение ![]() определяет
гиперболу с центром в точке
определяет
гиперболу с центром в точке ![]() и
полуосями
и
полуосями ![]() .
Оси данной гиперболы будут лежать на
прямых
.
Оси данной гиперболы будут лежать на
прямых ![]() .
Определим
параметр
.
Определим
параметр ![]() .
Тогда эксцентриситет будет
равен:
.
Тогда эксцентриситет будет
равен: ![]() .
Асимптотами
гиперболы будут прямые
.
Асимптотами
гиперболы будут прямые ![]() и
и ![]() ,
или, после очевидных
преобразований
,
или, после очевидных
преобразований ![]() и
и ![]() .
Директрисами
гиперболы будут прямые
.
Директрисами
гиперболы будут прямые ![]() ,
или, что то же самое, прямые
,
или, что то же самое, прямые ![]() .
.
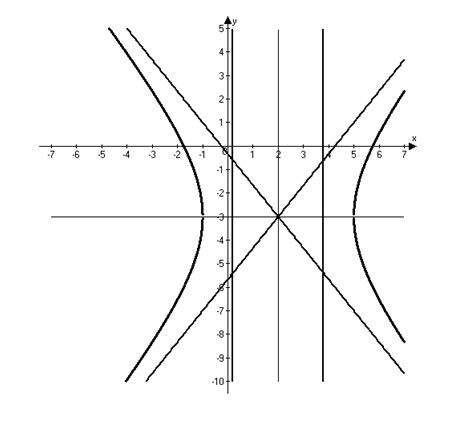
Билет №37
Угол между двумя плоскостями в пространстве связан с углом между нормалями к этим плоскостям 1 соотношением: = 1 или = 1800 - 1, т.е.
cos = cos1.
Определим угол 1. Известно, что плоскости могут быть заданы соотношениями:
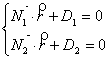 ,
где
,
где
![]() (A1, B1, C1),
(A1, B1, C1), ![]() (A2, B2, C2).
Угол между векторами нормали найдем из
их скалярного произведения:
(A2, B2, C2).
Угол между векторами нормали найдем из
их скалярного произведения:
 .
.
Таким образом, угол между плоскостями находится по формуле:

Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
взаимное
расположение плоскостей
Получим
условия параллельности или совпадения
двух плоскостей ![]() и
и ![]() заданных
общими уравнениями:
заданных
общими уравнениями:
Необходимым
и достаточным условием параллельности
или совпадения плоскостей (4.23) является
условие коллинеарности их
нормалей![]()
![]() Следовательно,
если плоскости (4.23) параллельны или
совпадают, то
Следовательно,
если плоскости (4.23) параллельны или
совпадают, то ![]() т.е.
существует такое число
т.е.
существует такое число ![]() что
что
и наоборот.
Плоскости
совпадают, если помимо этих условий
справедливо ![]() Тогда
первое уравнение в (4.23) имеет вид
Тогда
первое уравнение в (4.23) имеет вид ![]() т.е.
равносильно второму, поскольку
т.е.
равносильно второму, поскольку ![]()
Таким
образом, плоскости
(4.23) параллельны тогда и только тогда,
когда соответствующие коэффициенты
при неизвестных в их уравнениях
пропорциональны, т.е. существует такое
число ![]() что
что ![]()
![]()
![]() но
но ![]() Плоскости
(4.23) совпадают тогда и только тогда,
когда все соответствующие коэффициенты
в их уравнениях пропорциональны:
Плоскости
(4.23) совпадают тогда и только тогда,
когда все соответствующие коэффициенты
в их уравнениях пропорциональны:
![]() и
и
Условия параллельности и совпадения плоскостей (4.23) можно записать в виде
Отсюда следует критерий параллельности или совпадения двух плоскостей (4.23):
![]() или
или
Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.
Если
заданы уравнения параллельных плоскостей
 =0,
то расстояние между плоскостями можно
найти, используя следующую формулу
=0,
то расстояние между плоскостями можно
найти, используя следующую формулу

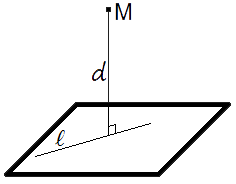
Расстояние от точки до плоскости - равно длине перпендикуляра, опущенного из точки на плоскость.
Если
задано уравнение плоскости
 , то расстояние от точки M(
, то расстояние от точки M(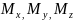 )
до
плоскости можно найти, используя
следующую формулу
)
до
плоскости можно найти, используя
следующую формулу

 Билеты№39
Угол
между прямыми в пространстве
Билеты№39
Угол
между прямыми в пространстве
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
Взаимное расположение прямой в пространстве
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
– прямые совпадают.
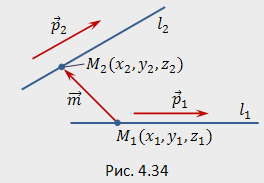
Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями
где ![]() —
точки, принадлежащие прямым
—
точки, принадлежащие прямым ![]() и
и ![]() соответственно,
a
соответственно,
a ![]()
![]() —
направляющие векторы (рис.4.34). Обозначим
через вектор, соединяющий заданные
точки.
—
направляющие векторы (рис.4.34). Обозначим
через вектор, соединяющий заданные
точки.
Перечисленным выше случаям взаимного расположения прямых и соответствуют следующие признаки:
–
прямые
и
скрещивающиеся ![]() векторы
векторы ![]() не
компланарны;
не
компланарны;
–
прямые
и
пересекаются
векторы
компланарны,
а векторы ![]() не
коллинеарны;
не
коллинеарны;
–
прямые
и
параллельные
векторы
коллинеарны,
а векторы ![]() не
коллинеарны;
не
коллинеарны;
– прямые и совпадают векторы коллинеарны.
Эти условия можно записать, используя свойства смешанного и векторного произведений. Напомним, что смешанное произведение векторов в правой прямоугольной системе координат находится по формуле:
Равенство нулю смешанного произведения векторов является необходимым и достаточным условием их компланарности. Поэтому:
– прямые и скрещивающиеся определитель отличен от нуля;
– прямые и пересекаются определитель равен нулю, а вторая и третья его строки не пропорциональны, т.е.
– прямые и параллельные вторая и третья строки определителя пропорциональны, т.е. а первые две строки не пропорциональны, т.е.
– прямые и совпадают все строки определителя пропорциональны, т.е.
Билет№ 40
Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.
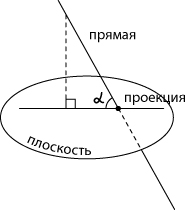

Теоремы
Если прямая, пересекающая плоскость, перпендикулярна двум прямым, лежащим в этой плоскости и проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
Если прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпердикулярна и самой наклонной.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, расположенной в этой плоскости, то она параллельна этой плоскости.
Если прямая параллельна плоскости, то она параллельна некоторой прямой на этой плоскости.
Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
Все точки прямой, параллельной плоскости, одинаково удалены от этой плоскости.
Билет 59. Определение функции как отображения множества способы задания функции: аналитический, табличный, графический.
Функция — математическое понятие, отражающее связь между элементами различных множеств.
В самом общем виде, функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Способы задания функций:
Функция может быть задана тремя способами: аналитическим, табличным и в виде графика.
1) Аналитический способ задания функции
Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента.
Примеры:
![]() ;
;
![]() ;
;
![]() ;
;
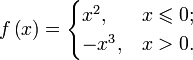
2) Табличный способ задания функций
Аргумент и вычисляемая функция записываются в таблицу. Форма таблицы может быть вертикальной или горизонтальной.
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Подобным образом создаются различные справочные таблицы для быстрого нахождения каких либо величин, выраженных аналитически, например, таблицы логарифмов, степеней, тригонометрических функций и т. д. или, как запись экспериментальных исследований, по которым может быть найдена эмпирическая формула или построен график.
3) Графический способ задания функций
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора.
Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
Билет 60. Свойства функции: область определения, множество значений, монотонность, экстремумы, периодичность, выпуклость и вогнутость графика функции, точки перегиба, асимптоты графика функции.
1) Область определения функции и область значений функции.
Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. Область значений функции - это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Множество значений функции.
Множество значений функции Е(y)- это множество всех значений, которые может принимать зависимая переменная y.
Чтобы
по графику
функции
![]() найти
ее множество значений, нужно, двигаясь
снизу вверх
вдоль оси OY,
записать все промежутки значений y, на
которых существует график функции.
найти
ее множество значений, нужно, двигаясь
снизу вверх
вдоль оси OY,
записать все промежутки значений y, на
которых существует график функции.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции.
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.
8) Точки максимума и минимума функции.
Точка
![]() называется
точкой
максимума
функции
,
если существует такая окрестность I
точки
,
что для любой точки х из этой окрестности
выполняется соотношение:
называется
точкой
максимума
функции
,
если существует такая окрестность I
точки
,
что для любой точки х из этой окрестности
выполняется соотношение:
![]() Графически
это означает что точка с абсциссой
лежит выше
других точек из окрестности I
графика функции
.
Графически
это означает что точка с абсциссой
лежит выше
других точек из окрестности I
графика функции
.
Точка называется точкой минимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
![]()
![]() Графически
это означает что точка с абсциссой
лежит ниже других точек из окрестности
I графика функции
.
Графически
это означает что точка с абсциссой
лежит ниже других точек из окрестности
I графика функции
.
Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.
9)Асимптоты графика функции
Вертикальная
асимптота — прямая вида
![]() при
условии существования предела
при
условии существования предела
![]() .
.
Горизонтальная
асимптота — прямая вида
![]() при
условии существования предела
при
условии существования предела
![]() .
.
Наклонная
асимптота — прямая вида
![]() при
условии существования пределов
при
условии существования пределов
Пример наклонной асимптоты
![]()
![]()
Билет 61. Основные элементарные функции и их свойства.
1.Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k x ,
где k - постоянная величина ( коэффициент пропорциональности ).
График
прямой
пропорциональности
– прямая линия, проходящая через начало
координат и образующая с осью X
угол
![]() ,
тангенс которого равен k
:
tan
=
k
( рис.8 ). Поэтому, коэффициент
пропорциональности называется также
угловым
коэффициентом.
На рис.8 показаны три графика для k
= 1/3, k
= 1 и k
= 3
.
,
тангенс которого равен k
:
tan
=
k
( рис.8 ). Поэтому, коэффициент
пропорциональности называется также
угловым
коэффициентом.
На рис.8 показаны три графика для k
= 1/3, k
= 1 и k
= 3
.
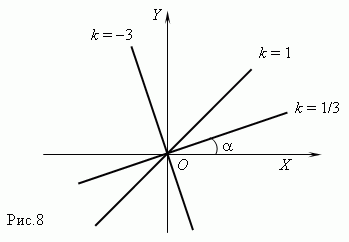
2. |
Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C ,
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
|
3. |
Обратная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k / x ,
где k - постоянная величина. График обратной пропорциональности – гипербола ( рис.10 ). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.
|
Основные характеристики и свойства гиперболы:
-
область определения функции:
x
![]() 0,
область значений:
y
0
;
0,
область значений:
y
0
;
- функция монотонная ( убывающая ) при x < 0 и при x > 0, но не
монотонная в целом из-за точки разрыва x = 0 ( подумайте, почему ? );
- функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
- нулей функция не имеет.
4. |
Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a 0. В простейшем случае: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
График функции y = ax 2 + bx + c - тоже квадратная парабола того же вида, что и y = ax 2, но её вершина лежит не в начале координат, а в точке с координатами:
|
|
5. |
Степенная
функция. Это функция: y = axn, где a, n
– постоянные. При n = 1 получаем прямую
пропорциональность: y = ax; при n = 2 -
квадратную параболу ; при n = -1 - обратную
пропорциональность или гиперболу.
Таким образом, эти функции - частные
случаи степенной функции. Мы знаем,
что нулевая степень любого числа,
отличного от нуля, равна 1, cледовательно,
приn = 0 степенная функция превращается
в постоянную величину: y = a, т.e. её
график - прямая линия, параллельная
оси Х, исключая начало координат
( поясните, пожалуйста, почему ? ). Все
эти случаи ( при a = 1 ) показаны на
рис.13 ( n
Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.
При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой. На
рис.16 представлена функция |
|
. |
6.Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81x имеет при x = 1/4 четыре различных значения: y = 3, y = -3, y = 3 i и y = -3 i (проверьте, пожалуйста !). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку ( 0, 1 ). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает.
Основные характеристики и свойства показательной функции: -
область определения функции: -
область значений: y > 0 ; - функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - нулей функция не имеет.
|
|
7. |
Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число, не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график ( рис.18 ) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Основные характеристики и свойства логарифмической функции: - область определения функции: x > 0, а область значений: < y+ ( т.e. y R ); - это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - у функции есть один ноль: x = 1. |
|
8. |
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция y = sin x представляется графиком ( рис.19 ). Эта кривая называется синусоидой. График
функции y
= cos x представлен
на рис.20; это также синусоида, полученная
в результате перемещения графика
y
= sin x вдоль
оси Х
влево на
Из этих графиков очевидны характеристики и свойства этих функций: -
область определения:
<
x +
область
значений: 1
- эти функции периодические: их период 2 ; - функции ограниченные ( | y | , всюду непрерывные, не монотонные, но имеющие так называемые интервалы монотонности, внутри которых они ведут себя, как монотонные функции ( см. графики рис.19 и рис.20 ); - функции имеют бесчисленное множество нулей
Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис.22
|
|
9. |
Обратные тригонометрические функции.
|
|
Функции y = Arcsin x ( рис.23 ) и y = Arccos x ( рис.24 ) многозначные, неограниченные; их область определения и область значений соответственно: 1 x +1 и < y + . Поскольку эти функции многозначные,не рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
Функции y = arcsin x и y = arccos x обладают следующими характеристиками и свойствами:
- у обеих функций одна и та же область определения: 1 x +1 ;
их области значений: /2 y /2 для y = arcsin x и 0 y для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arcsin x – возрастающая функция; y = arccos x – убывающая );
- каждая функция имеет по одному нулю ( x = 0 у функции y = arcsin x и
x = 1 у функции y = arccos x).
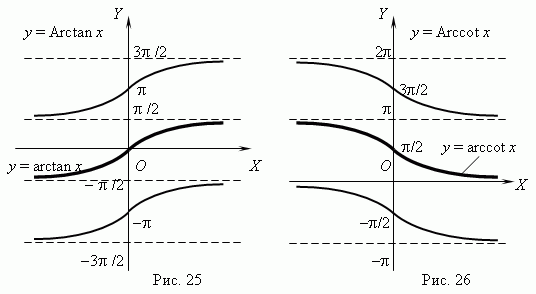
Функции y = Arctan x ( рис.25 ) и y = Arccot x ( рис.26 ) - многозначные, неограниченные; их область определения: x + . Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
Функции y = arctan x и y = arccot x имеют следующие характеристики и свойства:
- у обеих функций одна и та же область определения: x + ;
их области значений: /2 < y < /2 для y = arctan x и 0 < y < для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arctan x – возрастающая функция; y = arccot x – убывающая );
- только функция y = arctan x имеет единственный ноль ( x = 0 );
функция y = arccot x нулей не имеет.
62. Композиция функций. Сложная функция.
Композиция функций
Если
даны два отображения
![]() и
и
![]() ,
где
,
где
![]() ,
то имеет смысл "сквозное отображение"
,
то имеет смысл "сквозное отображение"
![]() из
из
![]() в
в
![]() ,
заданное формулой
,
заданное формулой
![]() ,
,
![]() ,
которое называется композицией
функций
,
которое называется композицией
функций
![]() и
и
![]() и
обозначается
и
обозначается
![]() .
.

Рис.1.30.Сквозное отображение из в
Таким
образом,
![]() ,
,
![]() при
всех
.
Другое название композиции -- сложная
функция (так
как сквозное отображение
при
всех
.
Другое название композиции -- сложная
функция (так
как сквозное отображение
![]() "сложено"
из отображений
"сложено"
из отображений
63.Обратимые функции. Обратная функция.
Пусть функция y=f(x), заданная на множестве X, обратима. Это значит, что функция f различным значениям аргумента ставит в соответствие различные значения функции, т.е. для любых x1,x2∈X : x1/=x2⇒f(x1)/=f(x2). В этом случае для каждого y∈Y=f(X) существует один и только один элемент x∈X такой, что y=f(x). А это означает, что на множестве Y определена функция g:Y→X , которую и называют обратной функцией к функции y=f(x) и обозначают: x=f−1(y). При этом очевидно, что функция f является обратной к функции f−1. Поэтому функции y=f(x) и x=f−1(y) называют взаимно обратными.
Т.о., если функция f:X→Y , где Y=f(X), обратима, то для нее существует единственная обратная функция f−1:Y→X и если y=f(x) то x=f−1(y), и если x=f−1(y), то y=f(x) и f−1(f(x))=x при любом x∈X , f−1(f(y))=y при любом y∈Y .
64. Числовые последовательности и действия с ними. Геометрическая и арифметическая прогрессии как числовые последовательности.
Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров x1,x2,...xn Числа x1,x2,...,xn — называются элементами последовательности, символ xn — общим элементом, а число n — его номером. Сокращенно последовательность обозначается символом {xn}.
Арифметическая прогрессия.
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.
Таким образом, арифметическая прогрессия – это числовая последовательность {an}, заданная рекуррентно соотношениями a1 = a, an = an–1 + d (n = 2, 3, 4, …) (a и d – заданные числа).
Геометрическая прогрессия.
Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.
Таким образом, геометрическая прогрессия – это числовая последовательность {bn}, заданная рекуррентно соотношениями b1 = b, bn = bn–1 q (n = 2, 3, 4…).
65.Предел числовой последовательности и его свойства. Сходимость числовой последовательностью. Критерий Коши. Переход к пределу в неравенствах.
Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству ê x n - a < .
![]() или
x n
a
или
x n
a
a- e < x n < a +
Последовательность {xn}, имеющая конечный предел а, называется сходящейся.
Сходящаяся последовательность имеет только один предел.
Критерий Коши сходимости последовательности
Для того чтобы последовательность {xn} сходилась, необходимо и достаточно, чтобы ∀ε >0 ∃номер n0 такой, что ∀n > n0 и любого p∈N выполнялось неравенство |xn+p - xn| <ε
66.Предел монотонной ограниченной последовательности.
Последовательность {xn} называется монотонно возрастающей, если для любого n xn+1 ³ xn.
1. Если последовательность {xn} монотонно возрастает (убывает) и ограничена сверху (снизу), то у нее существует конечный предел, равный sup{xn} ( inf{xn} ).
2 Если последовательность {xn} монотонно возрастает (убывает), но сверху (снизу) не ограничена, то у нее существует предел, равный +¥ ( -¥ ).
67. Предел функции в точке и на бесконечности. Различные определения предела функции. Односторонние пределы функции в точке.
Число А называется пределом функции у = f(х) в точке х = х0, если для любой последовательности значений аргумента {xn}, стремящейся к х0, т.е. xn→х0, соответствующая последовательность значений функции {f(xn)} стремится к числу А, т.е. f(xn)→A.
Предел
в точке обозначается:
 .
.
Существуют также односторонние пределы в точке - пределы слева и справа, когда значения аргумента приближаются к точке х=х0 со стороны больших или меньших значений:

Теорема. Для того чтобы функция имела у = f(х) имела предел в точке х=х0 необходимо и достаточно, чтобы в этой точке существовали равные между собой правый и левый пределы, которые и определяют предел функции в точке:

Число А называется пределом функции у = f(х) на бесконечности при х→∞, если для любой последовательности значений аргумента, стремящейся к бесконечности, т.е. xn→∞, соответствующая последовательность значений функции стремится к числу А, т.е. f(xn)→A.
Предел на бесконечности обозначается:
 .
.
Отметим, что функция может иметь пределы как на +∞, так и на -∞:
 .
.
68.Арифметические свойства предела функции.
Теорема об арифметических операциях над пределами:
Если
функции f(x)
и имеют конечные пределы в точке х=х0 или
на бесконечности при х
,
то
имеют конечные пределы в точке х=х0 или
на бесконечности при х
,
то
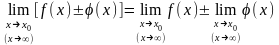 ;
;
 ;
;
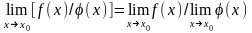 при условии
при условии
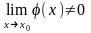 .
.
69.Бесконечно малые и бесконечно большие функции. Связь Бесконечно малых и бесконечно больших функций.
Определение:
Функция
 называется бесконечно малой в точке
х=х0 или на бесконечности при х,
если её пределы равны нулю:
называется бесконечно малой в точке
х=х0 или на бесконечности при х,
если её пределы равны нулю:
 .
.
Определение:
Функция
 называется бесконечно большой в точке
х=х0 или на бесконечности при х,
если её пределы равны бесконечности:
называется бесконечно большой в точке
х=х0 или на бесконечности при х,
если её пределы равны бесконечности: .
.
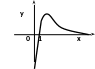
Следует
отметить, что одна и та же функция может
быть одновременно бесконечно малой или
бесконечно большой в разных точках. На
рисунке функция является бесконечно
малой в точке х=1 и при
 ,
а в точке х=0 эта функция является
бесконечно большой.
,
а в точке х=0 эта функция является
бесконечно большой.
Теорема о связи бесконечно малых или бесконечно больших функций:
Если
функция
является бесконечно малой в точке х=х0
или на бесконечности при х,
то функция
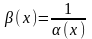 является бесконечно большой и наоборот,
если
- бесконечно большая функция, то
является бесконечно большой и наоборот,
если
- бесконечно большая функция, то
 является бесконечно малой функцией.
является бесконечно малой функцией.
72.Первый замечательный предел и его следствия.
Первый замечательный предел:
 или
или
 ,
,
где u=u(x)→0 при x→0
Следствия из первого замечательного предела:
 ;
;
 ;
;
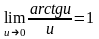 .
.
Пример.

73.Второй замечательный предел и его следствия.
Второй замечательный предел:
 или
или
 ,
,
где е 2.73…-натуральное число, а logex = lnx называется натуральным логарифмом.
Следствия из второго замечательного предела:
 ;
;
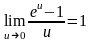 ;
;
 ;
;
 .
.
74.Непрерывность функции в точке. Различные подходы к определению понятия непрерывности функции в точке.
Определение
1. Функция
 называется непрерывной в точке
называется непрерывной в точке
 ,
если выполнены следующие три условия:
1)
,
если выполнены следующие три условия:
1)
 определена в точке
и ее окрестности; 2)
существует конечный предел функции
в точке
;
3)
этот предел равен значению функции в
точке
,
т. е.
определена в точке
и ее окрестности; 2)
существует конечный предел функции
в точке
;
3)
этот предел равен значению функции в
точке
,
т. е.

Так
как
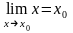 ,
то равенство (1) можно записать в виде
,
то равенство (1) можно записать в виде
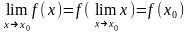
Это означает, что для непрерывной функции знаки предела и функции можно переставлять.
На практике часто используется следующее определение непрерывности функции в точке, эквивалентное определению 1.
Определение
2. Функция
называется непрерывной в точке
,
если: 1)
определена в точке
и ее окрестности; 2)
существует конечные односторонние
пределы
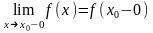 и
и
 ;
3)
эти пределы равны между собой и равны
значению функции в точке
,
т. е.
;
3)
эти пределы равны между собой и равны
значению функции в точке
,
т. е.

Сформулируем еще одно определение непрерывности функции, опираясь на понятия приращения аргумента и функции.
Пусть
функция
определена в точке
и ее окрестности. Дадим аргументу
приращение
 .
Тогда функция
получит приращение
.
Тогда функция
получит приращение
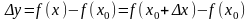 (рис. 1).
(рис. 1).
Определение 3. Функция называется непрерывной в точке , если: 1) определена в точке и ее окрестности; 2) бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:

75.Локальные свойства непрерывных функций. Непрерывность сложной и обратной функции. Непрерывность основных элементарных функций.
Локальные свойства непрерывных функций:
1.Пусть функция f:E R непрерывна в точке a. Тогда f(x) ограничена в некоторой окрестности точки a.
2.Пусть функция f(x) непрерывна в точке a и f(a) 0, то в некоторой окрестности точки a все значения функции положительны или отрицательны вместе с f(a).
3.Если f(x), g(x) - непрерывны в точке a, то функции: f(x)+g(x), f(x)g(x), f(x)/g(x) (при g(a) 0 ) непрерывны в точке a.
4.Если функция g(x):Y R непрерывна в точке b Y, а функция f:E Y непрерывна в точке a, f(a) = b, тогда композиция g° f также непрерывна в точке a.
Теорема
1. Пусть
функции f(x) и g(x) непрерывны в точке х0.
Тогда функция f(x) не равная g(x), f(x)g(x) и
![]() (если
g(x) не равно 0) непрерывны в точке x0.
(если
g(x) не равно 0) непрерывны в точке x0.
Доказательство.
Пусть
f(x) и g(x) непрерывны в точке x0.
Это значит, что
![]() .
Но тогда, по свойствам пределов
.
Но тогда, по свойствам пределов

Пусть функция (t) непрерывна в точке t0 и функция f(x) непрерывна в точке х0=(t0). Тогда функция f((t)) непрерывна в точке t0.
Доказательство.
Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем

Непрерывность элементарных функций
Все элементарные функции являются непрерывными в любой точке свой области определения. Функция называется элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя:
Алгебраические
многочлены
![]() ;
;
Рациональные
дроби
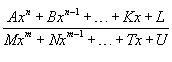 ;
;
Степенные
функции
![]() ;
;
Показательные
функции
![]() ;
;
Логарифмические
функции
![]() ;
;
Тригонометрические
функции
![]() ;
;
Обратные
тригонометрические функции
![]() ;
;
Гиперболические
функции
![]() ;
;
Обратные
гиперболические функции
![]() .
.
Билет 59. Определение функции как отображения множества способы задания функции: аналитический, табличный, графический.
Функция — математическое понятие, отражающее связь между элементами различных множеств.
В самом общем виде, функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Способы задания функций:
Функция может быть задана тремя способами: аналитическим, табличным и в виде графика.
1) Аналитический способ задания функции
Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента.
Примеры:
;
;
;
2) Табличный способ задания функций
Аргумент и вычисляемая функция записываются в таблицу. Форма таблицы может быть вертикальной или горизонтальной.
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Подобным образом создаются различные справочные таблицы для быстрого нахождения каких либо величин, выраженных аналитически, например, таблицы логарифмов, степеней, тригонометрических функций и т. д. или, как запись экспериментальных исследований, по которым может быть найдена эмпирическая формула или построен график.
3) Графический способ задания функций
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора.
Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
Билет 60. Свойства функции: область определения, множество значений, монотонность, экстремумы, периодичность, выпуклость и вогнутость графика функции, точки перегиба, асимптоты графика функции.
1) Область определения функции и область значений функции.
Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. Область значений функции - это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Множество значений функции.
Множество значений функции Е(y)- это множество всех значений, которые может принимать зависимая переменная y.
Чтобы по графику функции найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции.
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.
8) Точки максимума и минимума функции.
Точка называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
Графически это означает что точка с абсциссой лежит выше других точек из окрестности I графика функции .
Точка называется точкой минимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
Графически это означает что точка с абсциссой лежит ниже других точек из окрестности I графика функции .
Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.
9)Асимптоты графика функции
Вертикальная асимптота — прямая вида при условии существования предела .
Горизонтальная асимптота — прямая вида при условии существования предела
.
Наклонная асимптота — прямая вида при условии существования пределов
Пример наклонной асимптоты
Билет 61. Основные элементарные функции и их свойства.
1.Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k x ,
где k - постоянная величина ( коэффициент пропорциональности ).
График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол , тангенс которого равен k : tan = k ( рис.8 ). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = 3 .
2. |
Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C ,
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
|
3. |
Обратная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k / x ,
где k - постоянная величина. График обратной пропорциональности – гипербола ( рис.10 ). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.
|
Основные характеристики и свойства гиперболы:
- область определения функции: x 0, область значений: y 0 ;
- функция монотонная ( убывающая ) при x < 0 и при x > 0, но не
монотонная в целом из-за точки разрыва x = 0 ( подумайте, почему ? );
- функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
- нулей функция не имеет.
4. |
Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a 0. В простейшем случае: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
График функции y = ax 2 + bx + c - тоже квадратная парабола того же вида, что и y = ax 2, но её вершина лежит не в начале координат, а в точке с координатами:
|
|
5. |
Степенная функция. Это функция: y = axn, где a, n – постоянные. При n = 1 получаем прямую пропорциональность: y = ax; при n = 2 - квадратную параболу ; при n = -1 - обратную пропорциональность или гиперболу. Таким образом, эти функции - частные случаи степенной функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно, приn = 0 степенная функция превращается в постоянную величину: y = a, т.e. её график - прямая линия, параллельная оси Х, исключая начало координат ( поясните, пожалуйста, почему ? ). Все эти случаи ( при a = 1 ) показаны на рис.13 ( n 0 ) и рис.14 ( n < 0 ). Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции:
Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.
При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой. На рис.16 представлена функция . Эта функция является обратной к квадратной параболе y = x 2, её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла. Это способ получения графика любой обратной функции из графика её исходной функции. Мы видим по графику, что это двузначная функция (об этом говорит и знак ± перед квадратным корнем). Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю. |
|
. |
6.Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81x имеет при x = 1/4 четыре различных значения: y = 3, y = -3, y = 3 i и y = -3 i (проверьте, пожалуйста !). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку ( 0, 1 ). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает.
Основные характеристики и свойства показательной функции: - область определения функции: - < x < + ( т.e. x R ); область значений: y > 0 ; - функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - нулей функция не имеет.
|
|
7. |
Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число, не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график ( рис.18 ) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Основные характеристики и свойства логарифмической функции: - область определения функции: x > 0, а область значений: < y+ ( т.e. y R ); - это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - у функции есть один ноль: x = 1. |
|
8. |
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция y = sin x представляется графиком ( рис.19 ). Эта кривая называется синусоидой.
График функции y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на 2
Из этих графиков очевидны характеристики и свойства этих функций: - область определения: < x + область значений: 1 y +1; - эти функции периодические: их период 2 ; - функции ограниченные ( | y | , всюду непрерывные, не монотонные, но имеющие так называемые интервалы монотонности, внутри которых они ведут себя, как монотонные функции ( см. графики рис.19 и рис.20 ); - функции имеют бесчисленное множество нулей
Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис.22
|
|
9. |
Обратные тригонометрические функции.
|
|
Функции y = Arcsin x ( рис.23 ) и y = Arccos x ( рис.24 ) многозначные, неограниченные; их область определения и область значений соответственно: 1 x +1 и < y + . Поскольку эти функции многозначные,не рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
Функции y = arcsin x и y = arccos x обладают следующими характеристиками и свойствами:
- у обеих функций одна и та же область определения: 1 x +1 ;
их области значений: /2 y /2 для y = arcsin x и 0 y для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arcsin x – возрастающая функция; y = arccos x – убывающая );
- каждая функция имеет по одному нулю ( x = 0 у функции y = arcsin x и
x = 1 у функции y = arccos x).
Функции y = Arctan x ( рис.25 ) и y = Arccot x ( рис.26 ) - многозначные, неограниченные; их область определения: x + . Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
Функции y = arctan x и y = arccot x имеют следующие характеристики и свойства:
- у обеих функций одна и та же область определения: x + ;
их области значений: /2 < y < /2 для y = arctan x и 0 < y < для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arctan x – возрастающая функция; y = arccot x – убывающая );
- только функция y = arctan x имеет единственный ноль ( x = 0 );
функция y = arccot x нулей не имеет.
62. Композиция функций. Сложная функция.
Композиция функций
Если даны два отображения и , где , то имеет смысл "сквозное отображение" из в , заданное формулой , , которое называется композицией функций и и обозначается .
Рис.1.30.Сквозное отображение из в
Таким образом, , при всех . Другое название композиции -- сложная функция (так как сквозное отображение "сложено" из отображений
63.Обратимые функции. Обратная функция.
Пусть функция y=f(x), заданная на множестве X, обратима. Это значит, что функция f различным значениям аргумента ставит в соответствие различные значения функции, т.е. для любых x1,x2∈X : x1/=x2⇒f(x1)/=f(x2). В этом случае для каждого y∈Y=f(X) существует один и только один элемент x∈X такой, что y=f(x). А это означает, что на множестве Y определена функция g:Y→X , которую и называют обратной функцией к функции y=f(x) и обозначают: x=f−1(y). При этом очевидно, что функция f является обратной к функции f−1. Поэтому функции y=f(x) и x=f−1(y) называют взаимно обратными.
Т.о., если функция f:X→Y , где Y=f(X), обратима, то для нее существует единственная обратная функция f−1:Y→X и если y=f(x) то x=f−1(y), и если x=f−1(y), то y=f(x) и f−1(f(x))=x при любом x∈X , f−1(f(y))=y при любом y∈Y .
64. Числовые последовательности и действия с ними. Геометрическая и арифметическая прогрессии как числовые последовательности.
Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров x1,x2,...xn Числа x1,x2,...,xn — называются элементами последовательности, символ xn — общим элементом, а число n — его номером. Сокращенно последовательность обозначается символом {xn}.
Арифметическая прогрессия.
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.
Таким образом, арифметическая прогрессия – это числовая последовательность {an}, заданная рекуррентно соотношениями a1 = a, an = an–1 + d (n = 2, 3, 4, …) (a и d – заданные числа).
Геометрическая прогрессия.
Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.
Таким образом, геометрическая прогрессия – это числовая последовательность {bn}, заданная рекуррентно соотношениями b1 = b, bn = bn–1 q (n = 2, 3, 4…).
65.Предел числовой последовательности и его свойства. Сходимость числовой последовательностью. Критерий Коши. Переход к пределу в неравенствах.
Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству ê x n - a < .
или x n a
a- e < x n < a +
Последовательность {xn}, имеющая конечный предел а, называется сходящейся.
Сходящаяся последовательность имеет только один предел.
Критерий Коши сходимости последовательности
Для того чтобы последовательность {xn} сходилась, необходимо и достаточно, чтобы ∀ε >0 ∃номер n0 такой, что ∀n > n0 и любого p∈N выполнялось неравенство |xn+p - xn| <ε
66.Предел монотонной ограниченной последовательности.
Последовательность {xn} называется монотонно возрастающей, если для любого n xn+1 ³ xn.
1. Если последовательность {xn} монотонно возрастает (убывает) и ограничена сверху (снизу), то у нее существует конечный предел, равный sup{xn} ( inf{xn} ).
2 Если последовательность {xn} монотонно возрастает (убывает), но сверху (снизу) не ограничена, то у нее существует предел, равный +¥ ( -¥ ).
67. Предел функции в точке и на бесконечности. Различные определения предела функции. Односторонние пределы функции в точке.
Число А называется пределом функции у = f(х) в точке х = х0, если для любой последовательности значений аргумента {xn}, стремящейся к х0, т.е. xn→х0, соответствующая последовательность значений функции {f(xn)} стремится к числу А, т.е. f(xn)→A.
Предел в точке обозначается: .
Существуют также односторонние пределы в точке - пределы слева и справа, когда значения аргумента приближаются к точке х=х0 со стороны больших или меньших значений:
Теорема. Для того чтобы функция имела у = f(х) имела предел в точке х=х0 необходимо и достаточно, чтобы в этой точке существовали равные между собой правый и левый пределы, которые и определяют предел функции в точке:
Число А называется пределом функции у = f(х) на бесконечности при х→∞, если для любой последовательности значений аргумента, стремящейся к бесконечности, т.е. xn→∞, соответствующая последовательность значений функции стремится к числу А, т.е. f(xn)→A.
Предел на бесконечности обозначается:
.
Отметим, что функция может иметь пределы как на +∞, так и на -∞:
.
68.Арифметические свойства предела функции.
Теорема об арифметических операциях над пределами:
Если функции f(x) и имеют конечные пределы в точке х=х0 или на бесконечности при х , то
;
;
при условии .
69.Бесконечно малые и бесконечно большие функции. Связь Бесконечно малых и бесконечно больших функций.
Определение: Функция называется бесконечно малой в точке х=х0 или на бесконечности при х, если её пределы равны нулю:
.
Определение: Функция называется бесконечно большой в точке х=х0 или на бесконечности при х, если её пределы равны бесконечности: .
Следует отметить, что одна и та же функция может быть одновременно бесконечно малой или бесконечно большой в разных точках. На рисунке функция является бесконечно малой в точке х=1 и при , а в точке х=0 эта функция является бесконечно большой.
Теорема о связи бесконечно малых или бесконечно больших функций:
Если функция является бесконечно малой в точке х=х0 или на бесконечности при х, то функция является бесконечно большой и наоборот, если - бесконечно большая функция, то является бесконечно малой функцией.
72.Первый замечательный предел и его следствия.
Первый замечательный предел:
или ,
где u=u(x)→0 при x→0
Следствия из первого замечательного предела:
;
;
.
Пример.
73.Второй замечательный предел и его следствия.
Второй замечательный предел:
или ,
где е 2.73…-натуральное число, а logex = lnx называется натуральным логарифмом.
Следствия из второго замечательного предела:
;
;
;
.
74.Непрерывность функции в точке. Различные подходы к определению понятия непрерывности функции в точке.
Определение 1. Функция называется непрерывной в точке , если выполнены следующие три условия: 1) определена в точке и ее окрестности; 2) существует конечный предел функции в точке ; 3) этот предел равен значению функции в точке , т. е.
Так как , то равенство (1) можно записать в виде
Это означает, что для непрерывной функции знаки предела и функции можно переставлять.
На практике часто используется следующее определение непрерывности функции в точке, эквивалентное определению 1.
Определение 2. Функция называется непрерывной в точке , если: 1) определена в точке и ее окрестности; 2) существует конечные односторонние пределы и ; 3) эти пределы равны между собой и равны значению функции в точке , т. е.
Сформулируем еще одно определение непрерывности функции, опираясь на понятия приращения аргумента и функции.
Пусть функция определена в точке и ее окрестности. Дадим аргументу приращение . Тогда функция получит приращение (рис. 1).
Определение 3. Функция называется непрерывной в точке , если: 1) определена в точке и ее окрестности; 2) бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
75.Локальные свойства непрерывных функций. Непрерывность сложной и обратной функции. Непрерывность основных элементарных функций.
Локальные свойства непрерывных функций:
1.Пусть функция f:E R непрерывна в точке a. Тогда f(x) ограничена в некоторой окрестности точки a.
2.Пусть функция f(x) непрерывна в точке a и f(a) 0, то в некоторой окрестности точки a все значения функции положительны или отрицательны вместе с f(a).
3.Если f(x), g(x) - непрерывны в точке a, то функции: f(x)+g(x), f(x)g(x), f(x)/g(x) (при g(a) 0 ) непрерывны в точке a.
4.Если функция g(x):Y R непрерывна в точке b Y, а функция f:E Y непрерывна в точке a, f(a) = b, тогда композиция g° f также непрерывна в точке a.
Теорема 1. Пусть функции f(x) и g(x) непрерывны в точке х0. Тогда функция f(x) не равная g(x), f(x)g(x) и (если g(x) не равно 0) непрерывны в точке x0.
Доказательство.
Пусть f(x) и g(x) непрерывны в точке x0. Это значит, что . Но тогда, по свойствам пределов
Пусть функция (t) непрерывна в точке t0 и функция f(x) непрерывна в точке х0=(t0). Тогда функция f((t)) непрерывна в точке t0.
Доказательство.
Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем
Непрерывность элементарных функций
Все элементарные функции являются непрерывными в любой точке свой области определения. Функция называется элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя:
Алгебраические многочлены ;
Рациональные дроби ;
Степенные функции ;
Показательные функции ;
Логарифмические функции ;
Тригонометрические функции ;
Обратные тригонометрические функции ;
Гиперболические функции ;
Обратные гиперболические функции .
Билет 76. Односторонняя непрерывность.
Определение односторонней непрерывности.
В
определении непрерывности функции в
точке х0 требуется существование
![]() и равенство
и равенство![]() . С применением односторонних пределов
определяются понятия непрерывности
функции в точке слева и справа:
. С применением односторонних пределов
определяются понятия непрерывности
функции в точке слева и справа:
Функция
f(x)
называется непрерывной в точке х0 слева,
если![]()
Функция
f(x)
называется непрерывной в точке х0 справа,
если![]()
Если одно из этих условий не выполнено, то функция f(x) имеет в точке х0 разрыв, соответственно, слева или справа. Если функция определена на отрезке [a,b], то в левом конце отрезка х0= a можно говорить только о непрерывности справа, в правом конце (х0= b) - о непрерывности слева. Для внутренней точки отрезка функция f(x) непрерывна в точке х0 тогда и только тогда, когда она непрерывна в этой точке слева и справа
Билет 77.Точки разрыва и их классификация
Определение точки разрыва
Точка Х0 называется точкой разрыва функции f(x), если она определена в некоторой проколотой окрестности точки X0 (то есть определена на некотором интервале, для которого X0 служит внутренней точкой, но в самой точке X0, возможно, не определена) и выполняется хотя бы одно из следующих условий:
1) не
существует предела слева![]()
2) не
существует предела справа![]()
3)
пределы слева![]() и
справа
и
справа![]() существуют
и равны друг другу
существуют
и равны друг другу![]() ,но
не совпадают со значением функции в
точке X0:
,но
не совпадают со значением функции в
точке X0:
![]()
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
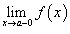 и
правосторонний предел
и
правосторонний предел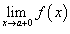
Эти односторонние пределы конечны
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:

Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу
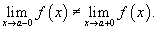
Такая
точка называется точкой конечного
разрыва. Модуль разности значений
односторонних пределов![]() называется
скачком функции.
называется
скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
Билет 78.Определение и свойства функции, непрерывной на отрезке: ограниченность, существование наибольшего и наименьшего значений, промежуточные значения. Теорема об обратной функции.
1)Определение.
Функцию f(x) называют непрерывной на отрезке [а, b], если она непрерывна в каждой точке интервала (а, Ь) и, кроме того, непрерывна справа в точке а и непрерывна слева в точке b.
2)Свойства функций, непрерывных на отрезке
Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.
Теорема 2 (существование наибольшего и наименьшего значений). Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.
Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x1 Î [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x1) ≥ f(x). Аналогично найдётся такая точка x2, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x1) ≤ f(x).
Теорема 3(промежуточн значения). Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C.
3)Теорема об обратной функции
Пусть функция y = f(x) определена, строго монотонна и непрерывна на отрезке [a,b]. Тогда на отрезке [α, β] ( α = f(a), β = f(b) ) cуществует обратная функция x = g(y), также строго монотонная и непрерывная на отрезке (α, β).
Билет 80.Приращение аргумента. Приращение функции. Определение производной функции. Геометрический и механический смысл производной.
Рассмотрим
некоторую функцию y
= f
( x
) в двух точках x0
и x0
+![]() : f
( x0
) и f
( x0
+
). Здесь через
обозначено некоторое малое изменение
аргумента, называемое приращением
аргумента; соответственно разность
между двумя значениями функции: f
( x0
+
) - f
( x0
) называется приращением функции.
Производной функции y
= f
( x
) в точке x0
называется предел:
: f
( x0
) и f
( x0
+
). Здесь через
обозначено некоторое малое изменение
аргумента, называемое приращением
аргумента; соответственно разность
между двумя значениями функции: f
( x0
+
) - f
( x0
) называется приращением функции.
Производной функции y
= f
( x
) в точке x0
называется предел:

Определение производной функции.
Производной функции y=f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю:
LimΔx→0 (Δf(x0)/Δx)=limΔx→0 ((f(x+Δx)-f(x0))/Δx)=f`(x0)
Геометрический смысл производной:
угловой коэффициент касательной равен производной функции в точке касания
Билет 81.Правила дифференцирования. Призводные основных элементарных функций.
1)Правила дифференцирования
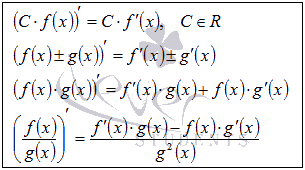
2)Производные основных элементарных функций.

Билет 82,83,84,85….Я вложила файл.Там всё доступно написано))просто у меня нет такой программы,что бы от туда норм скопировать в ворд.у меня копируется,но иироглифами какими то.
Билет 86.Производная показательно-степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Показательно-степенная
функция (точнее, сложно-показательная
функция) — это функция вида
![]()
то есть функция, в которой переменная содержится и в основании степени, и в ее показателе.
Билет 87.Производные высших порядков
Пусть
y=f(x)
– некоторая дифференцируемая функция,
производная от которой
![]() также является дифференцируемой
функцией. Производная функции
также является дифференцируемой
функцией. Производная функции
![]() обозначается символическим выражением
обозначается символическим выражением
![]() и называется второй производной (или
производной второго порядка) функции
f(x)
:
и называется второй производной (или
производной второго порядка) функции
f(x)
:
![]()
Запись
вида:
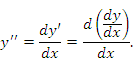
позволяет
указать в явной форме переменную, по
которой выполняется дифференцирование
функции. Однако такое обозначение
является достаточно громоздким и поэтому
обычно используется его сокращенная
форма:
![]()
Производной
n-го порядка от функции f(x)
называется производная от производной
(n - 1)-го порядка:
![]()
Верхний
индекс n,
заключенный в круглые скобки, указывает
порядок производной. Например, пятую
производную от функции y
записывают в виде
![]() Для
обозначения производных до третьего
порядка включительно обычно предпочитают
использовать штрихи
Для
обозначения производных до третьего
порядка включительно обычно предпочитают
использовать штрихи![]() или
или![]()
Билет 88.Дифференциал функции как главная линейная часть приращения функции.Свойства и геометрический смысл дифференциала функции.
1)Выражение
вида f’(x)*дельта
X-называется
ГЛАВНОЙ ЧАСТЬЮ ПРИРАЩЕНИЯ ФУНКЦИИ ИЛИ
ДИФФЕРЕНЦИАЛОМ ФУНКЦИИ.
обозначение![]()
2)
Геометрический
смысл дифференциала. Дифференциал
функции y = f(x) равен приращению ординаты
касательной, проведённой к графику этой
функции в точке (x; y), при изменении xна
величину
![]()
3)Свойства
![]()
![]()
![]()
Билет90.Правила нахождения дифференциала функции.
Основные правила нахождения дифференциала
1. Дифференциал постоянной величины dc=0.
2. Дифференциал сумм d(u+v)=du+dv.
3. Дифференциал произведения d(d·u)=du·v+dv·u
4. Дифференциал частного
5. Дифференциал сложной функции y=f (u); u=f(x);dy=f ΄(u)·dxu.
Билет 92.Приближённые вычисления с помощью дифференциала
формулу![]() задающую
определение дифференциала, можно
записать в виде приближённого
равенства
задающую
определение дифференциала, можно
записать в виде приближённого
равенства![]() если
считать значение бесконечно малой
величины
если
считать значение бесконечно малой
величины![]() много
меньшим, чем
много
меньшим, чем![]() .Перенося
.Перенося![]() в
правую часть, получаем:
в
правую часть, получаем:
![]() где
где![]() .С
учётом выражения дифференциала через
частные производные, находим, что
.С
учётом выражения дифференциала через
частные производные, находим, что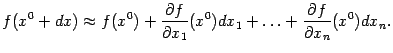
Эту
формулу можно применять для приближённого
вычисления значений функции
f
в
точках
,если
известны значения f
и
её частных производных![]() ,в
точке X0
,в
точке X0
Билет94.Исследование функции с помощью производной.
Общая схема исследования функции:
1. Найти область определения функции и исследовать поведение
функции в граничных точках этой области (при стремлении
аргумента к границе области). Найти вертикальные асимптоты.
2. Выяснить симметрию графика (четность или нечетность функции)
и вопрос о периодичности функции.
3. Найти точки разрыва и промежутки непрерывности.
4. Определить нули (корни) функции и промежутки знакопостоянства.
5. Найти точки и значения экстремумов и промежутки монотонности.
6. Найти точки перегиба и интервалы выпуклости.
7. Найти наклонные асимптоты графика функции.
8. Указать другие специфические особенности функции.
9. Построить график функции.
И + приложение.