1.2. Методика расчета среднего ресурса машины (тс), ско, доверительных границ.
1. Определение ресурса статистическим методом. Для определения среднего ресурса машины (ТС, изделия, агрегата) действуют следующим образом. Выбирают несколько (N) машин (выборка k=1, , N ), которые в процессе эксплуатации (или испытаний) доводят до предельного состояния. Тем самым, определяют величину ресурса pk для каждой машины (элемента).
Ресурс – это случайная величина, поэтому ее основные параметры (среднее и дисперсия, или СКО) определяются по известным правилам. Обычно считается, что эта случайная величина распределена по нормальному закону распределения, что соответствует логике центральной предельной теоремы (много воздействующих причин с малым влиянием каждой из них).
Как известно, для более точной оценки параметров генеральной совокупности, оцениваемая выборка должна быть как можно больше, однако это невыгодно с практической точки зрения. Поэтому, как мы увидим ниже, всегда следует добиваться разумного компромисса между точностью определения ресурса и его трудоемкостью, стоимостью и длительностью.
Стандартным методом проводятся точечные оценки ресурса, то-есть оцениваются средний ресурс, его дисперсия, и СКО:
,
(1)
.
(2)
Очевидно, что достаточно точные оценки требуют большого числа машин, на которых определяется ресурс.
Полученные
точечные оценки позволяют установить
нижнюю
и верхнюю
доверительные границы для среднего
ресурса
с соответствующей доверительной
вероятностью Р (двусторонней). По этой
вероятности (уровню значимости)
определяется коэффициент Стьюдента t
(где число степеней свободы k
= N
– 1), после чего доверительные границы
по известным формулам :
(3)
Пример 1. При наблюдении за 9 автомобилями были установлены следующие пробеги (тыс. км) до предельного состояния:
45, 60, 50, 50, 60, 65, 70, 70, 100 .
Результат расчетов: = 62.2 тыс. км. S = 17 тыс. км..
Для Р = 0.95 имеем k = N – 1 = 8, t = 2.306 , что приводит к
= 49.2 тыс. км., а = 75.2 тыс. км..
Полученный интервал разброса пробега слишком велик. Уменьшить можно увеличением выборки. Следует отметить, что на практике используют только нижнюю границу среднего ресурса.
Мы
знаем, что средний ресурс машины
приближается к точному значению ресурса
(его матожиданию) с увеличением количества
N
машин, поставленных на испытания. При
этом СКО этой разницы (
)
уменьшается с увеличением N
как
. Поэтому при увеличении N
уменьшаются доверительные границы при
определении среднего ресурса. Поэтому
возникает задача о необходимом обьеме
выборки для заданной точности определения
среднего ресурса. Метод приближенного
определения обьема выборки описан ниже.
Определение заданного обьема выборки для требуемой точности разброса пробега при заданной доверительной вероятности Р.
Обозначая
=
t
S
/
; (4)
определяем число необходимых для испытаний машин (ТС)
(5)
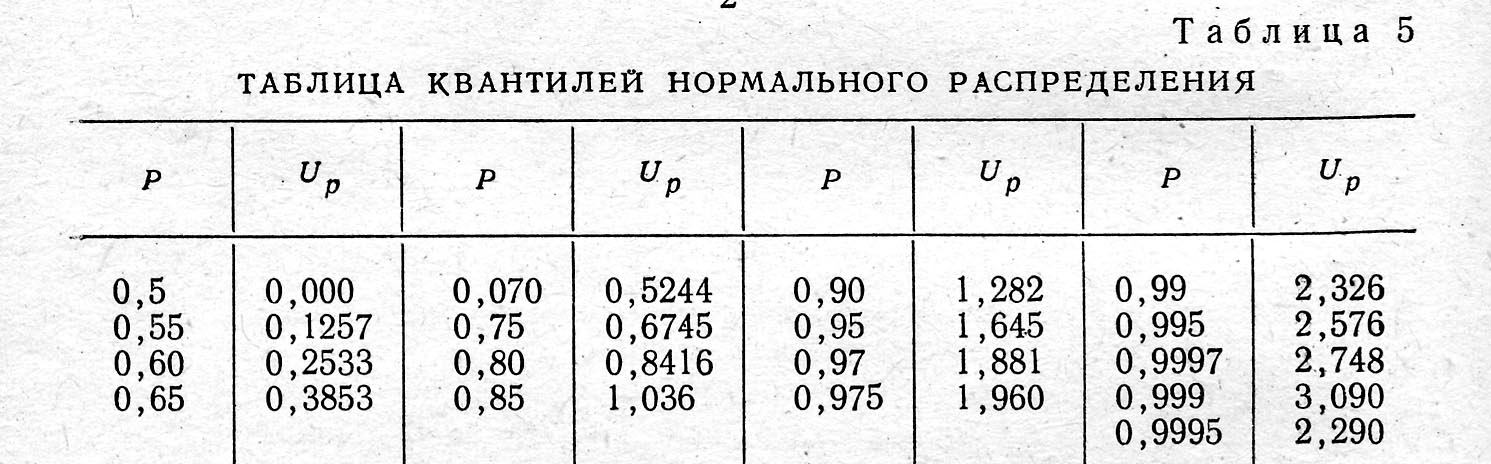
Здесь U - вспомогательная величина, зависящая от принятой доверительной вероятности. Эта величина может быть найдена по таблице квантилей нормального распределения для значения вероятности Р1 = (1 + Р) / 2.
Пример 2. В условиях предыдущего примера определим необходимое число автомобилей, при этом = 5 тыс. км.. Р1 = 0.975, а U = 1.960 , что приводит к N = 45 автомобилей.
Часто,
при определении средних ресурсов
элементов машин можно принять в пределах
/
0.05 – 0.1.
В лаб. Работе 2 реализуется указанная процедура определения среднего ресурса, доверительных границ для него, и вычисление необходимого числа машин для испытаний.
Таким образом, статистический метод определения ресурса позволяет решить эту задачу с точки зрения физического изнашивания, так как эксплуатационные данные отражают именно эту сторону явлений.
Следует отметить, что если под ресурсом подразумевается временная наработка (временной ресурс), то тогда для обозначения ресурса вместо буквы Р применяется обозначение ТР (связанное со словом – время по английски – time).
К определению оптимальной долговечности машин можно подойти и по другому.