ТФКП2009 / Лекция 41

Лекция 41. Производная функции комплексного переменного.

П.1 Производная и ее геометрический смысл.

ОПР. Производной функции в точке называется предел

= (1)

ТЕОРЕМА 1. Функция дифференцируема в смысле С ( моногенна) в точке в том и только в том случае, если у нее существует производная в этой точке.

ДОК. Если функция дифференцируема в смысле С, то и .

Тогда существует . Пусть существует производная (1), тогда

, т.е. функция дифференцируема.

Если функция дифференцируема в смысле , то

. (2)

Если при фиксированном , то и из (2) следует

Предел - есть производная функции в точке

по направлению определяемым аргументом . Эта производная существует для любой дифференцируемой в смысле функции. Если функция дифференцируема в смысле С, производная по направлению не зависит от , () и равна производной . В частности, при .

Пусть , - гладкая кривая в области на комплексной плоскости С , - голоморфная в функция, , и кривая в области на комплексной плоскости W.

Если ,то ,, - параметрические уравнения кривой на плоскости. Параметрические уравнения кривой имеют вид : .

Если получает приращение , то направление вектора секущей , , , при стремится к направлению касательной к кривой в точке . Соответствующий вектор в образе, где , , при стремится по направлению к касательному вектору к кривой в точке . Если , то из существования предела следует, что . Здесь - угол наклона

с положительным направлением оси OU касательной к кривой в точке В, угол

наклона с положительным направлением оси ОХ касательной к кривой в точке А.

Отсюда вытекает ГЕОМЕТРИЧЕСКИЙ СМЫСЛ аргумента производной :

Аргумент производной функции комплексного переменного есть угол, который составляют касательная к любой гладкой кривой в точке и касательной к кривой образа в точке .

Если другая гладкая кривая, проходящая через точку , то . Тогда вычитая, получим , т.е. углы между кривыми в образе и в прообразе одинаковые. Это одно из важных свойств преобразований комплексной плоскости, называемых конформными.

Из существования производной функции в точке вытекает, что

. Последнее указывает на ГЕОМЕТРИЧЕСКИЙ СМЫСЛ модуля производной : модуль комплексной производной – это число в пределе равное отношению расстояния между образами двух точек и при отображении к расстоянию их прообразов, точек и , т.е. коэффициенту растяжения комплексной плоскости функцией в точке . Дифференцируемая функция производит его равномерно по направлению, т.е. независимо от аргумента .

ОПР. Линейное отображение , задаваемое формулой

, (3)

называется касательным к дифференцируемому в смысле отображению

: в точке .

Если функция : дифференцируема в смысле С, то касательное отображение примет вид :

. (4)

Отображение (4) сводится к преобразованию подобия с коэффициентом и повороту на угол против часовой стрелки. Такое преобразование

1) сохраняет углы , 2) переводит окружность в окружность , 3)переводит квадрат в квадрат.

ОПР. Дифференцируемое в смысле отображение называется конформным в точке , если касательное к нему отображение сохраняет ориентацию и удовлетворяет условиям 1) -3).

Сохранение ориентации означает следующее : если направление обхода любого треугольника выбрано таким, что следуя ему треугольник остается слева ( положительное направление ), то направление обхода вершин образа треугольника также положительное.

ОПР. Отображение : конформно в области , если оно однолистно и

конформно в каждой точке .

Если отображение в точке дифференцируемо в смысле С и , то оно , как было показано выше, конформное в этой точке . Справедливо и обратное утверждение . Действительно, если отображение конформно , то образом комплексных чисел и являются числа , . С учетом сохранения углов : ,

т.е. дифференцируемая функция в смысле С.

Отображение отличается от касательного (4) в окрестности точки членами порядка , поэтому оно сохраняет углы с точность до бесконечно малых более высокого порядка, чем , преобразует окружность почти в окружность, квадрат в почти квадрат.

П.2 Линейная функция ().

Дифференцируемая, однолистная на плоскости С функция. Отображение , соответствующее линейной функции , является композицией параллельного

переноса на вектор , поворота на угол и преобразования подобия с коэффициентом . Каждое из этих преобразований сохраняет ориентацию , углы , переводит окружность в окружность и прямую в прямую, поэтому преобразование осуществляемое линейной функцией конформно на плоскости С.

ПРИМЕР 1. Найти линейную функцию, отображающую круг на круг .

РЕШЕНИЕ. Отображение переводит круг в единичный круг с центром в начале координат. Отображение переводит в . Тогда композиция отображений : .

П.3 Дробно-линейная функция .

А. Начнем с функции .

ОПР. Преобразование In плоскости называется инверсией относительно единичной окружности с центром в точке О (начало координат), если образом точки является точка , лежащая на луче ОМ и такая, что .

Соответствующее инверсии преобразование комплексной плоскости описывается

формулой : или .

Отметим некоторые свойства преобразования инверсии.

1. Если А, В, С – вершины треугольника на плоскости, их образы при отображении In , то треугольники АВС и подобны (углы при соответствующих вершинах равны) и противоположно ориентированы. Отсюда следует, что инверсия сохраняет углы и меняет ориентацию на противоположную.

2. Инверсия отображает открытый единичный круг с центром в точке О во внешность круга. Граница круга (единичная окружность) остается неподвижной.

3. Образом произвольной окружности К с центром в точке , не проходящей через точку О, является окружность . Пусть точки пересечения луча с окружностью К. Тогда окружностьпостроена на отрезке как на диаметре. Если окружность К проходит через точку О, то прямая (окружность

бесконечного радиуса) перпендикулярная лучу и проходящая через точку , где - точка пересечения луча с окружностью К.

4. Образом произвольной прямой, не проходящей через точку О, является окружность , проходящая через точку О.

Отображение = является композицией инверсии относительно единичной окрестности с центром в начале координат () и симметрии () относительно оси ОХ.

Поскольку симметрия также как и инверсия изменяет ориентацию на противоположную , отображение сохраняет ориентацию и является конформным на плоскости С

( )

Образом бесконечно удаленной точки при отображении является и наоборот.

Конформность отображения в точке связывают с конформностью отображения в точке . В данном случае, - дифференцируемая функция в точке и , поэтому функция однолистная на и конформно отображает .

Б. Дробно-линейную функцию ( можно представить в виде :

.

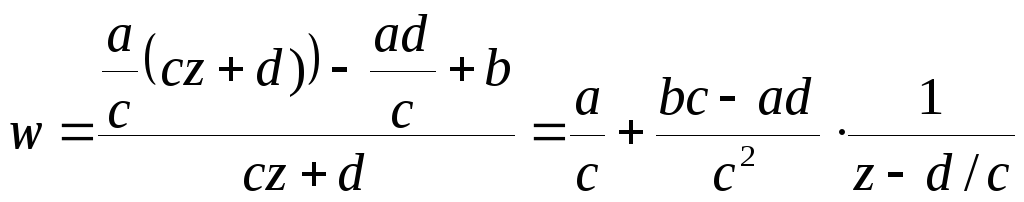Поэтому преобразование ,осуществляемое дробно-линейной функцией, можно представить цепочкой преобразований :

1) ( параллельный перенос) 2) ( инверсия плюс симметрия)

3) (подобие плюс поворот) 4) ( параллельный перенос ).

Преобразования параллельного переноса, подобия, поворота на угол (против часовой стрелки) являются конформными, инверсия плюс симметрия относительно оси ОХ

также конформно (пункт А). Тогда преобразование, осуществляемое дробно-линейной

функцией, также однолистное , конформное на замкнутой комплексной плоскости .

ПРИМЕР 2. Найти дробно-линейную функцию, отображающую единичный круг на верхнюю полуплоскость : .

РЕШЕНИЕ. Рассмотрим последовательность преобразований : 1)

(переводит в круг ) 2) ( инверсия плюс симметрия, переводит

в полуплоскость ) 3) ( параллельный перенос, переводит

полуплоскость : ) 4) ( поворот на 90⁰ против часовой стрелки, переводит в ) . Объединяя преобразования 1) - 4) , получим функцию, отображающую круг на верхнюю полуплоскость .

ВОПРОСЫ К ЭКЗАМЕНУ.

1) Производная функции комплексного переменного. Связь между моногенностью функции в точке и существованием у нее производной. Производная по направлению.

2) Геометрический смысл модуля и аргумента производной.

3) Конформные отображения в точке, связь понятий конформности в точке и

моногенности функции. Конформность линейного отображения на С.

4) Дробно-линейная функция . Конформность отображения, осуществляемого

невырожденной дробно-линейной функцией, на .