
- •Вопрос 1: ProjectExpert и его применение
- •Тема 1 Моделирование как средство оценки эффективности капиталовложений в проекты в условиях меняющего рынка.
- •1. Методика unido.
- •2. Задачи и средства финансового моделирования
- •Тема 2: Возможности пакета ProjectExpert
- •1.Общее описание пакета
- •2.Инвестиционный план
- •3.Операционный план
- •4.Финансирование проекта
- •Тема 3: Анализ эффективности проекта в системе
- •1.Вкладка "Результаты"
- •2.Вкладка “Анализ проекта”
- •3. Вкладка Актуализация
- •Тема 4. Экономические модели, используемые в ProjectExpert.
- •1.Модель определения объема производства продукции предприятия
- •1.1 Простой случай
- •1.2. Учет налога на прибыль, уточненная модель.
- •1.3. Точка безубыточности
- •1.4. Точка безубыточности в пакете ProjectExpert.
- •2. Модели обслуживания кредитов
- •2.1. Способы начисления процентов.
- •2.2. Способы погашения долгов
- •Тема 5: Специфика экономического обоснования программных проектов.
- •1. Актуальность задачи экономического обоснования в производстве программ
- •2. Специфика производства программного обеспечения
- •3. Особенности экономики производства крупных программных продуктов
- •Тема 6: Типичный порядок экономического обоснования программных проектов.
- •1. Выбор жизненного цикла разработки по
- •1.1 Каскадная (водопадная) модель
- •1.2 Итеративная и инкрементальная модель – эволюционный подход
- •1.3 Спиральная модель
- •2. Отбор команды разработчиков проекта
- •3. Создание структуры пооперационного перечня работ
- •4. Оценка размера и возможности повторного использования по
- •5. Оценка длительности и стоимости разработки по
- •6. Создание бизнес-плана
- •Вопрос 2: Более сложные модели, чем используемые в ProjectExpert
- •Тема 7. Экономические модели поведения потребителя.
- •2. Функция полезности и её свойства
- •Тема 10. Эвристические методы построения функции полезности
- •2. Метод анализа иерархий (маи) для формирования оценок ряда трудноформализуемых факторов
- •Тема 11. Теория потребительского спроса.
- •1. Товары – заменители, предельные нормы замещения
- •2 Задача оптимизации выбора потребителя
- •3 Функция спроса
- •4 Уравнение Слуцкого
- •Тема 8. Производитель и его поведение.
- •1. Общие понятия.
- •3. Производственные функции и их свойства.
- •Тема 9. Теория фирмы
- •1. Задача производителя
- •2 Функция спроса на ресурсы
- •3 Характер функции предложения продукции
- •Тема 10: Термодинамика как модель динамики экономических систем
- •1 Отличия экономических и тепловых систем
- •2. Характеристика систем, ценности ресурсов.
- •3. Равновесные экономические циклы.
Тема 9. Теория фирмы
1. Задача производителя
1.1. Постановка задачи фирмы.
Пусть P-вектор цен, если T=(X,Y)-технология, где X-затраты, Y- выпуск, то скалярное произведение векторов P*T= Px*X+Py*Y есть прибыль от использования технологии T (все компоненты вектора X: xi<0).
Аксиома
производителя: производитель выбирает
технологию T из своего
производств-го мн-ва ,
стремясь максимиз-ть прибыль
![]() –
> max (1.1)
–
> max (1.1)
По опред-ю компонента Y (объем выпуска) для решения T, такого, что удовл. условие (1.1), будет лежать на кривой производственных возможностей.
Выпуск фирмы Y можно охарак-ть:
1) Либо объемом выпуска, ели выпускается 1 товар (наш случай).
2) Либо суммарной стоимостью выпуска, если товаров много.
В нашем случае затраты X однозначно определяют Y посредством производственной ф-ии Y=f(X), где X=(X1,…,Xn).
Пусть - это цена единицы выпускаемой продукции. Тогда, W-прибыль есть ф-я от X и .
При постоянном прибыль W есть функция только от X. Тогда в этом случае можно записать: W(X)= *Y-P*X=*f(X)-P*X
Определяем задачу фирмы: W(X)= *f(X)-P*X – > max, при X>=0.
1.2. Решение задачи фирмы.
Исходя
из условий экстремума, приравниваем
частные производные W к
0. Исходя из этого, получим
![]() (1.2) или в векторном виде:
(1.2) или в векторном виде:
![]() .
.
Для
простоты будем считать, что всякий xi>0,
т. к. нулевые затраты можно просто
исключить из рассмотрения. Тогда точка
![]() ,
удовлетворяющая соотношению (1.2), является
точкой экстремума. а поскольку имеет
место отрицательная определенность
матрицы Гессе, т. е. вторые производные
предполагаются <0.
,
удовлетворяющая соотношению (1.2), является
точкой экстремума. а поскольку имеет
место отрицательная определенность
матрицы Гессе, т. е. вторые производные
предполагаются <0.
![]() ,то
выполняется условие максимума
(у
min вторая производная
>0).
,то
выполняется условие максимума
(у
min вторая производная
>0).
Оптимальный
выпуск продукции, соответствующий
найденной оптимальной точке
имеет
вид:
![]() .
Точка
или
.
Точка
или
![]() называется
оптимальным решением задачи фирмы.
называется
оптимальным решением задачи фирмы.
1.3. Экономический смысл решения задачи фирмы.
Поясним
экон. смысл соотношения (1.2). Ранее
определялись
![]() - вектор предельных продуктов, где
отдельная частная производная
- вектор предельных продуктов, где
отдельная частная производная
![]() - это i-й предельный продукт
или отклик выпуска на изменение i-го
товара – затрат (или ресурсов).
- это i-й предельный продукт
или отклик выпуска на изменение i-го
товара – затрат (или ресурсов).
Тогда,
![]() - это стоимость i-го
предельного продукта дополнительно
получаемого из кол-ва
- это стоимость i-го
предельного продукта дополнительно
получаемого из кол-ва
![]() единиц
i-го ресурса.
единиц
i-го ресурса.
Стоимость
доп. привлекаемых ресурсов
есть величина
![]() (1.3). Умножив левую и правую часть выраж-я
(1.2), задающего оптимальный объем выпуска,
на
(1.3). Умножив левую и правую часть выраж-я
(1.2), задающего оптимальный объем выпуска,
на
![]() ,
имеем:
,
имеем:
![]() (1.4).
(1.4).
Вывод: в точке оптимума стоимость затрат (выраж. (1.3)) равна стоимости приращения продукции (выраж. (1.4)). В данной точке мы не получим никакого выиграша от увеличения затрат по i-му ресурсу на величину .
Соотношение (1.2) задает точку равновесия. В данной точке нельзя извлечь из товаров-ресурсов больше, чем было потрачено на их покупку. Т. е. наращивании е объемов произв-ва при увеличении ресурсов идет до тех пор, пока не начнет выполн-ся соотнош-е (1.2).
2 Функция спроса на ресурсы
Исходя из предложенного подхода, можно построить ф-ии спроса на ресурсы для оптимального выпуска. При условиях (т.е.в обл. Е):
1)
![]()
2)
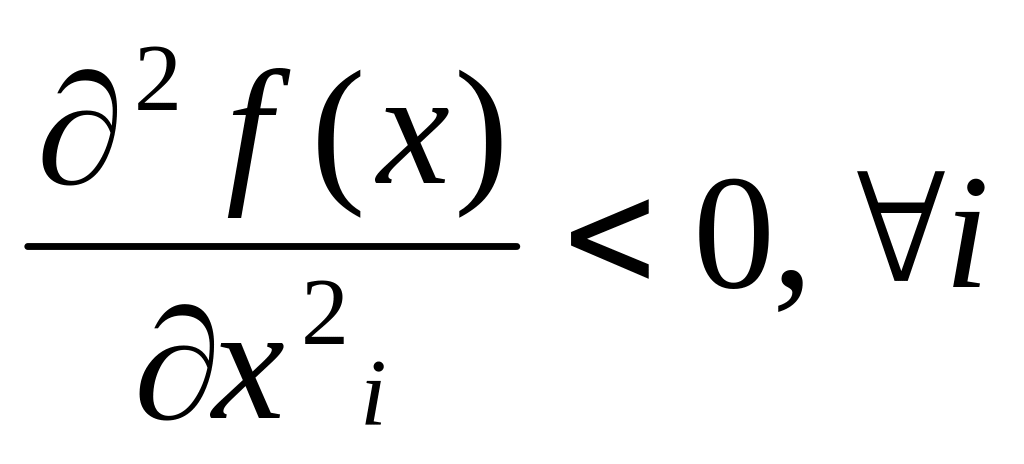
Решение
задачи фирмы
единственно для всякого >0
и p>0. Всякой паре (,P)
соответствует одно значение
.
След-но, имеет место ф-я:
![]() или
на компонентном уровне вектора X:
или
на компонентном уровне вектора X:
![]() .
все такие ф-ии наз. ф-ми спрося на ресурсы
при данных ценах на продукцию и ресурсы.
Перебрав возможные комбинации (,P)
и построив данные ф-ии (путем регрессии
по точкам как полином) и подставив
полученную ф-ю в производственную ф-ю
f(x), получим
ф-ю предложения продукции:
.
все такие ф-ии наз. ф-ми спрося на ресурсы
при данных ценах на продукцию и ресурсы.
Перебрав возможные комбинации (,P)
и построив данные ф-ии (путем регрессии
по точкам как полином) и подставив
полученную ф-ю в производственную ф-ю
f(x), получим
ф-ю предложения продукции:
![]()
